Unit 6
Design of Control System Using State Space
Q1) A system is described by 
=
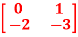B=
C=[1 0] . Y = [1 0]. Check the controllability of the system.
A1) [s] =[B AB]
= 
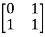
≠ 0 hence system is controllable.
Q2) A system is described by 
=
B=
C=[1 0] . Y = [1 0]. Check the observability of the system.
A2) AT= 
CT=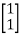
[Q]=[CT ATCT]
=
=
=
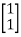
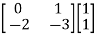
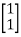
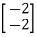
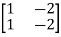
=0
=0 hence not observable.
Q3) The state equation of the system is given below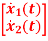 
= 
+ 
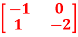
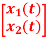u(t) . Y = [1 2]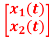
Comment on controllability.
A3) A=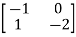 
B= 
Order of matrix n=2
[S] = [B AB]
=
= 
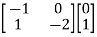
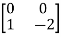
|S|= 0. Hence, system is not controllable.
Q4) The state space representation of a second order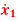 
= -x1+u and 
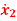= x1-2x2+u. State whether the system is controllable or not.
A4)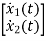 
= 
+ 
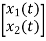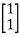u(t)
Order of matrix is n=2
[S] = [B AB]
=
= 
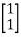
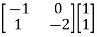
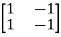
|S|= 0. Hence, system is not controllable.
Q5) A linear second order single input continuous time system is described as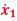 
= -2x1(t)+4x2(t) and 
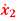= 2x1(t)-x2(t)+u(t). Comment on controllability.
A5)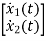 
= 
+ 
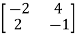
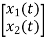u(t)
Order of matrix is n=2
[S] = [B AB]
=
= 
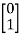
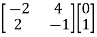
≠ 0 hence system is controllable.
Q6) Find the controllable canonical realization of the following systems H(s)=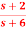
A6) H(s)=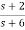
Let H(s)=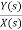
=
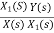H1(s)=
1/s+6
X(s)=sX1(s)+6X1(s)
SX1(s)= X(s) +6X1(s)
We can get X1(s) by passing sX1(s) through integrator. The above equation can be realised as
H2(s)=
s+2
Similarly, Y(s)= sX1(s)+2X1(s)
H2(s)=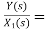
s+2
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
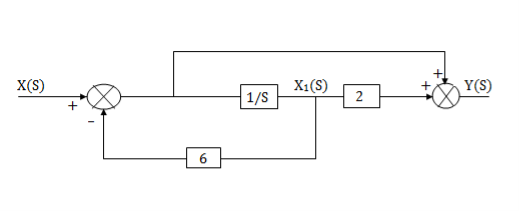
Q7) Find the controllable canonical realization of the following systems H(s)=
A7) H(s)=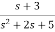
Let H(s)=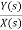
= 
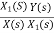
=s+3
Y(s)=sX1(s)+3X1(s)
The above transfer function can be realised as
Now,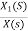 
=
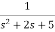
s2X1(s)=X(s)-2sX1(s)-5X1(s)
Assuming s2X1(s) is available the above transfer function can be realised as
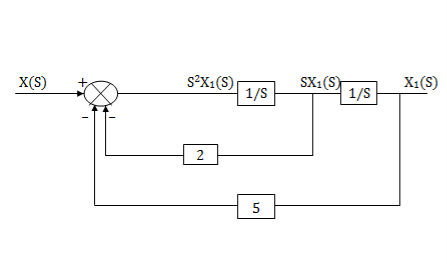
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
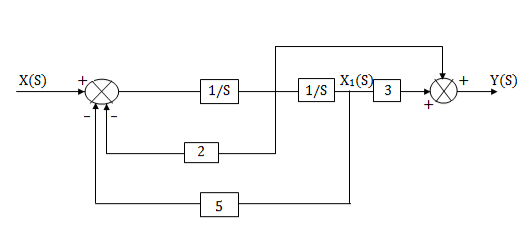
Q8) The closed loop transfer function is given as T(s)=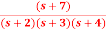
. Calculate the state model.
A8) The transfer function can be simplified using partial fraction method as
=
+ 
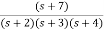s+7=A[s2+7s+12] +B[s2+6s+8] +C[s2+5s+6]
Equating coefficients of s2 from both sides
A+B+C=0
Equating coefficients of s from both sides
7A+6B+5C=1
Equating coefficients of s0 from both sides
12A+8B+6C=7
Solving above equations and finding values of A, B and C
A=5/2
B=-4
C=3/2
The transfer function will be
T(s)=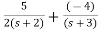
+ 
=
+ 
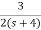
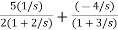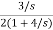
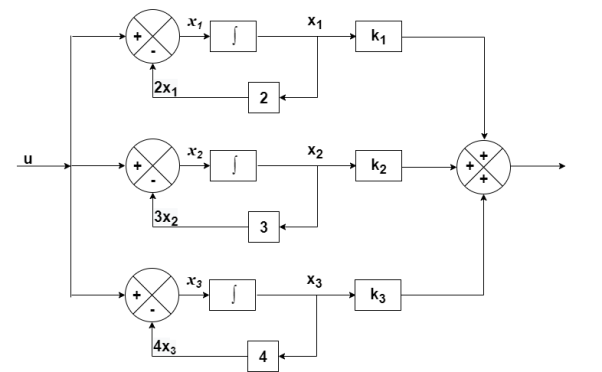
The output equation will be
y=k1x1+k2x2+k3x3
y=[k1 k2 k3]
[5/2 -4 3/2]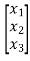
C=[5/2 -4 3/2]
D=[0]
The state equation is given as
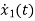=u(t)-2x1
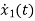=-2x1+u(t)
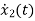=-3x2+u
= -4x3+u
Therefore
=
+
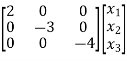[u]
A=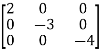
B=
Q9) What is the effect of pole zero cancellation on the controllability and observability of the system?
A9) For an nth order system with distinct eigenvalues the transfer function be
T(s)=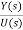
=[b0sm+b1sm-1+….+bm-1s+bm/[sn+a1sn-1+……..+an-1s+an]
=K(s-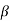
1)( s-
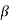2)…….( s-
m)/(s-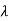
1)( s-
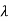2)……( s-
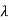n)
= 
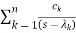
ck are residue poles at s=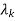
If the transfer function has identical pair of poles and zeros at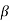 
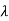i= 
i
The effect of this cancellation of pole and zero on observability and controllability depends on the property of state variable.
- If the state variable is of the form below , then ci=0 will appear in control vector B and the state is uncontrollable.
= 
+ 
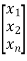u
y=[1 1 1……..1]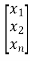
+b0u
- On the other-hand if the state variables are of the form
= 
+
y=[c1 c2 c3…….. cn]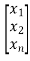
+b0u
Then then ci=0 will appear in output vector C and the state is shielded from observations.
- In LTI system if it has pole zero cancellation, the system will either be not controllable nor observable. But if the transfer function does not have any pole zero cancellations than the system can be represented by completely controllable and observable state model.
Q10) Consider a system 
=Ax(t)+Bu(t)
y=Cx
Where A=
B=
C=[0 1]. Design a full order stet observer, assuming that eigenvalues of the observer matrix are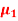 
=-1.8+j2.4 and 
=-1.8-j2.4?
A10) The characteristic equation of the system is given as
|sI-A|=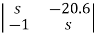
=s2-20.6=s2+a1s+a2=0
a1=0
a2=-20.6
The desired characteristic equation is given as
(s-
)(s-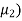
………(s-
=(s+1.8+j2.4)(s+1.8-j2.4)= s2+3.6s+9=s2+a1s+a2=0
a1=3.6
a2=9
The observer gain matrix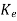 
is given as
=(WN*)-1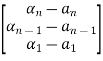
For above case we can write
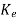=(WN*)-1
=
=
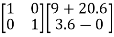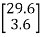
Q11) The closed loop transfer function is T(s)=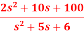 
. Find the state equation.
A11) Here the number of poles = number of zeros
T(s)=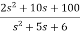
=
=
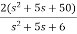
=2+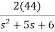 
=2+
Solving above by partial fraction method
88= As+2A+Bs+3B
A=-B
2A+3B=88
A=-88
B=88
The transfer function becomes
T(s)= 2-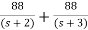
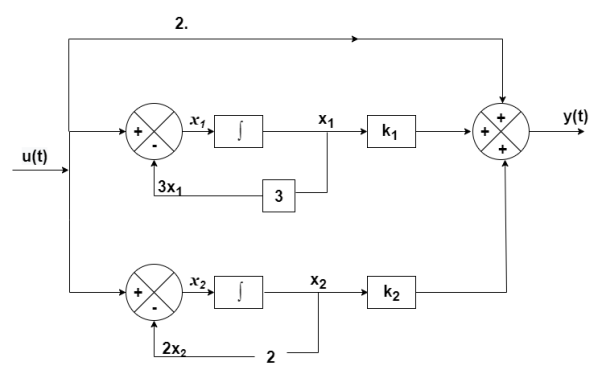
The output equation will be
y(t)=2U+k1x1+k2x2
y=[-88 88]
+[2]u
The output equation will be
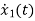=u(t)-3 x1
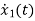=-3x1+u(t)
=-2x2+u(t)
Therefore, the state equation is given as
=
+
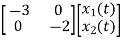A=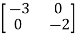
B=
