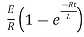UNIT 1
Linear Differential Equations (LDE) and Applications
Q1) Solve the equation y’’’+11y’-5y=0
A1)
The characteristic equation of the give D.E is
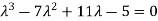
Here one of the root is 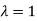 then factorising the term
then factorising the term 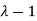 from the equation we obtain
from the equation we obtain
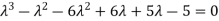
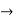 (
(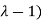 (
(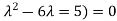
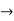 (
(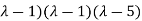 =0
=0
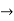 (
(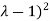 (
(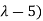 =0
=0
Thus the equation has two roots 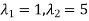
Hence the general equation of the D.E is
Y(x)=(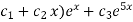
Where 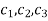 are arbitrary constants.
are arbitrary constants.
Q2) Solve 
A2) The given equation can be written in the symbolic form as-
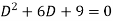
So that A.E is 
Hence the complete solution is-
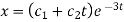
Q3) Determine the complementary function for the following D.E
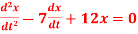 at t=0,1
at t=0,1
A3)
We can write the given homogeneous equation as follows
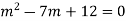
The auxiliary equation is 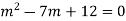
By factorising the auxiliary equations we get,
(m-3)(m-4)=0
And the two real solutions are m=3,4
Hence the complementary function is,
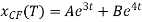
Since f(t) = 2 then 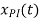 = c
= c
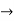 12c=2
12c=2
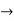 c=1/6 and
c=1/6 and 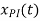 = 1/6
= 1/6
Therefore the general solution is
X(t) = 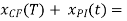
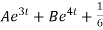
Q4) Solve 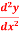 -
-
Given y=4 ,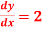 when x=0
when x=0
A4)
The auxiliary equation is
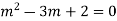
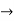 (m-1)(m-2)=0
(m-1)(m-2)=0
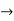 m=1,2
m=1,2
Therefore complimentary function is,
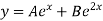
The particular integral is given by y=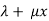

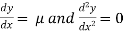
Substituting the above values in given equation we get,
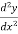 -
- = 0-3
= 0-3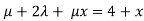
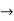 by comparing the co-efficients we get 2
by comparing the co-efficients we get 2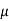 =1
=1 
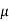 = ½
= ½
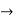 -3
-3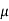 + 2
+ 2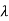 = 4+x
= 4+x
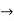
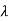 = 11/4
= 11/4
Therefore P.I is,
11/4+(1/2)x
General solution is, y = A + 11/4 +1/2x
+ 11/4 +1/2x
Q5) Find P.I of 
A5) P.I. = 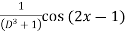
Put 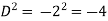
= 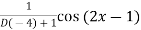
Multiply and divide by 1+4D
= 
= 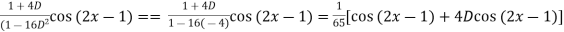
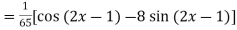
Q6) Find P.I. Of 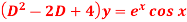
A6) P.I = 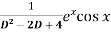
Replace D by D+1
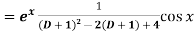
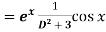
Put 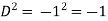
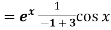

Q7) Solve the following by using the method of variation of parameters.
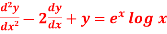
A7) This can be written as-
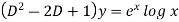
C.F.-
Auxiliary equation is- 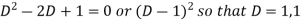
So that the C.F. Will be- 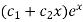
P.I.-
Here 
Now 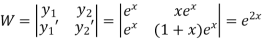
Thus PI = 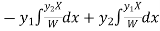
= 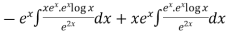
= 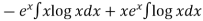
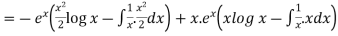
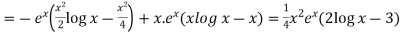
So that the complete solution is-
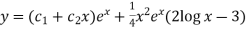
Q8) Solve 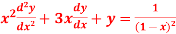
A8) On putting 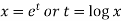 so that,
so that,
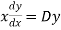 and
and 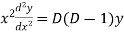
The given equation becomes-
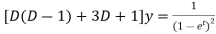
Or it can be written as-
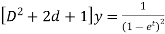
So that the auxiliary equation is- 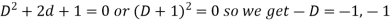
C.F. = 
Particular integral- 
Where 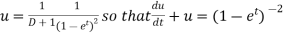
It’s a Leibnitz’s linear equation having I.F.= 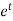
Its solution will be-
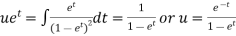
P.I. = 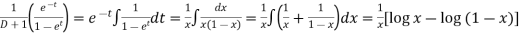
= 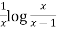
So that the complete solution is-
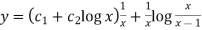
Q9) Solve the following simultaneous differential equations-
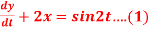

Given that x(0)=1 and y(0)= 0
A9)
Consider the given equations,

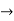 Dy +2x = sin2t
Dy +2x = sin2t
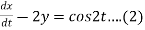
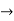 Dx -2y = cos2t
Dx -2y = cos2t
By solving the above equations we get,
(D2 +4)Y =0
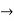
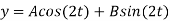
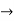
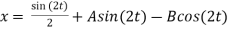
X(0) = 1, y(0) = 0
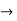 A =0, B=-1
A =0, B=-1

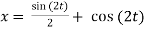
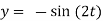
Q10) Finding the optimal current of an electrical circuit (RL circuits) in which the initial
Condition is i=0 at t=0
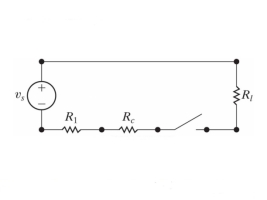
A10)
By Kirchhoff voltage law (KVL) method, we get
The differential equation for the RL circuit will be 
In which initial conditions are i=0 at t=0
The standard form of the equation is,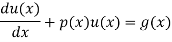
Dividing the differential equation by L to obtain
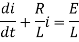
The integrating factor is
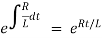
Multiplying the above equation with standard form gives rise to
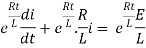
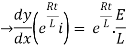
By applying integration on both sides we get
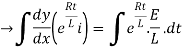

Now applying i=0 at t-0 gives us
0=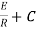
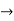 C=-
C=-
NOW
i=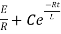
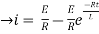
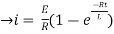 = t
= t 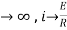
Therefore by finding current of the RL circuits is i=