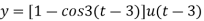UNIT 2

Laplace Transform

Q1) Find the Laplace transform of (1 + cos 2t)

A1)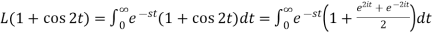

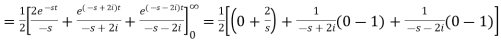
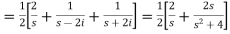
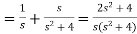
So that-

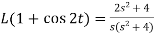
Q2) Find the Laplace transform of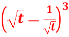

A2) Here-

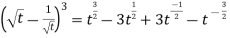
So that-

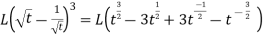
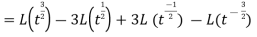
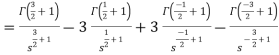
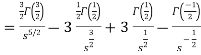
As we know that-  

So that-

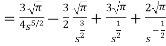
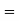
Hence-

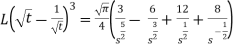
Q3) Find the Laplace transform of the following function-

A3) The given function f(t) can be written as-

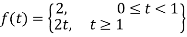
So that, by definition,

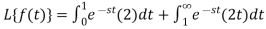
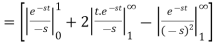
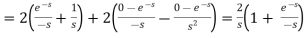
Q4) Find the Laplace transform of the following function (Half-wave rectifier)-

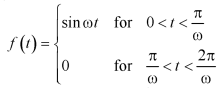
A4) By the definition-

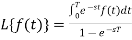
f(t) is a periodic function and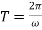

So that-

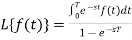
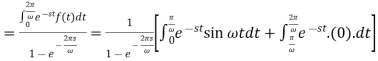
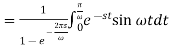
As we know that-

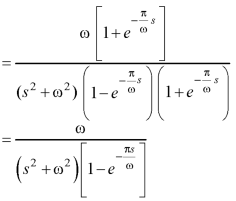
Q5) Find the Laplace transform of the periodic function-

A5) By the definition-

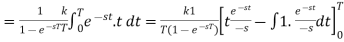
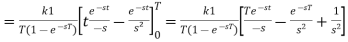
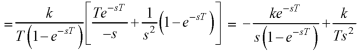
Q6) Find the Laplace transform of .

A6) Here-

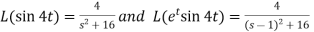
Now-

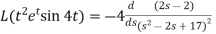
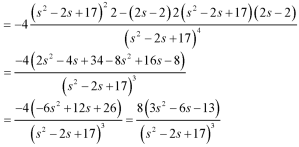
Q7) Find the Laplace transform of the following function by using unit step function-

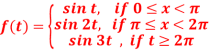
A7)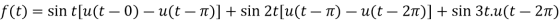

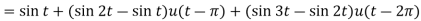
Since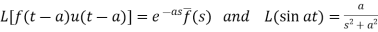

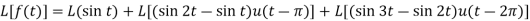
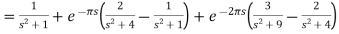
Q8) Find the Laplace transform of

Where-

A8) Here we are given—

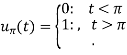
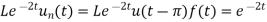
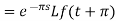
As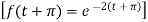

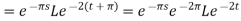
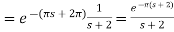
Q9) Evaluate-

1.

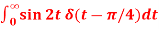
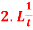
A9)1. As we know that-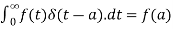 

So that-

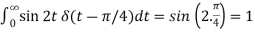
2. As we know that-

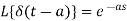
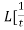
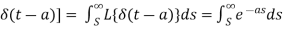
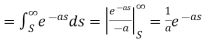
Q10) Use Laplace transform method to solve the following equation-

A10) Here we have-

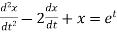
Take Laplace transform of both sides, we get-

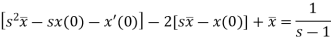
It becomes-

(

So that-

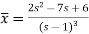
Now breaking it into partial fractions-

We get the following results on inversion-

Q11) Find the solution of the initial value problem by using Laplace transform-

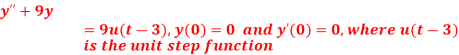
A11) Here we have-

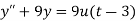
Taking Laplace transform, we get-

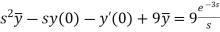
Putting the given values, we get-

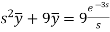
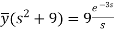
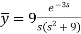
On inversion, we get-

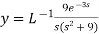
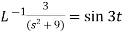
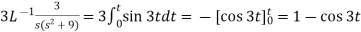4

Now-