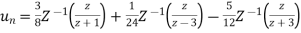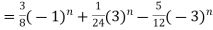UNIT 3

Fourier and Z-Transforms

Q1) Using complex form, find the Fourier series of the function

f(x) = sinx =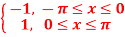

A1)

We calculate the coefficients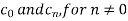

  =

=

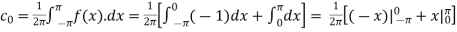
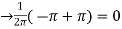
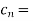
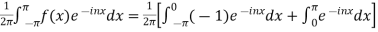
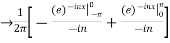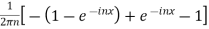
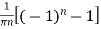
Hence the Fourier series of the function in complex form is

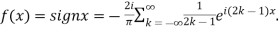
We can transform the series and write it in the real form by renaming as

n=2k-1,n=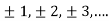

=

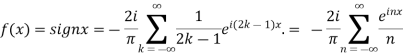
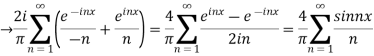
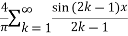
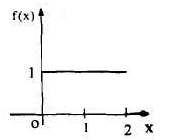
Q2) Find the fourier integral representation of the function

A2)

The graph of the function is shown in the below figure  satisfies the hypothesis of

Theorem -1 . Hence from Eqn,(5) and (6), we have

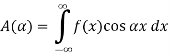
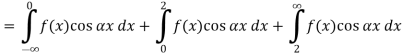
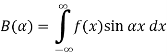
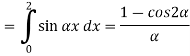
Substituting these coefficients in Eqn.(4) we obtain

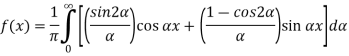
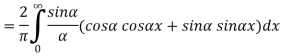
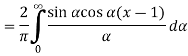
This is the Fourier integral representation of the given function.

Q3) Find the Fourier cosine integral of , where x>0, k>0 hence show that

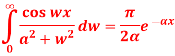
A3)

The Fourier cosine integral of f(x) is given by:

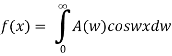
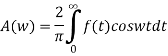
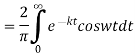
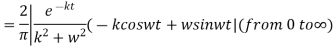
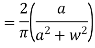
Q4) Find the Fourier transform of-

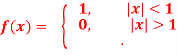
Hence evaluate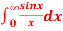

A4) As we know that the Fourier transform of f(x) will be-

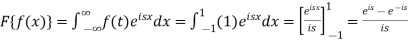
So that-

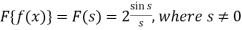
For s = 0, we get- F(s) = 2

Hence by the inverse formula, we get-

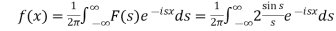
Putting x = 0, we get

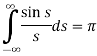
So-

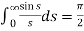
Q5) Find the Fourier transform of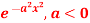

A5) As we know that the Fourier transform of f(x) will be-

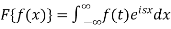
So that-

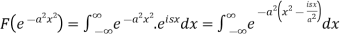
Now put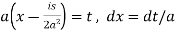

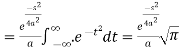
So that-

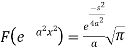
Q6) Find the Fourier cosine transform of-

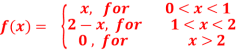
A6) We know that the Fourier cosine transform of f(x)-

=  

= 

=

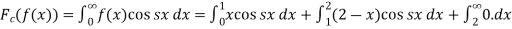
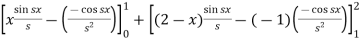
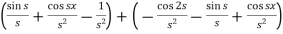
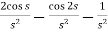
Q7) Find the Fourier sine transform of

A7) Let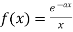                    

Then the Fourier sine transform will be-

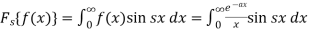
Now suppose,

Differentiate both sides with respect to x, we get-

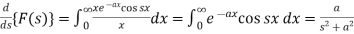      ……. (1)

On integrating (1), we get-

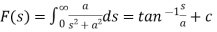
Q8) Find Z-transform of the following functions-

(i)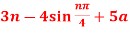

(ii)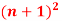

A8)i)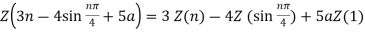 

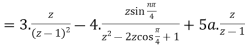
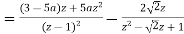
(ii)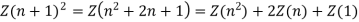

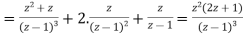
Q9) Solve the differential equation 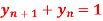 by z-transformation method.

A9)

Given,

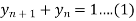
Let y(z) be the z-transform of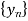

Taking z-transforms of both sides of eq(1) we get,

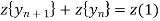
Ie.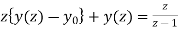

Using the given condition ,it reduces to

(z+1)y(z) =

Ie.

Y(z) =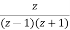

Or Y(Z) =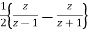

On taking inverse Z-transforms, we obtain

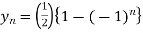
Q10) Solve the following by using Z-transform

A10) If 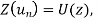then

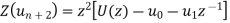
And

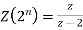
Now taking the Z-transform of both sides, we get

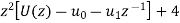z[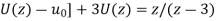

It becomes-

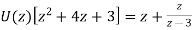
So that,

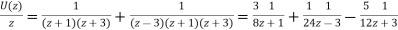
Now-

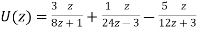
On inversion, we get-