Unit-5

Vector Calculus

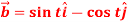Q1) If and then find-

1.

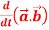
2.

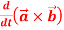
A1) 1. We know that-

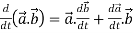
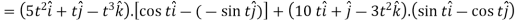
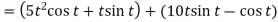
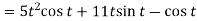
2.

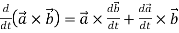
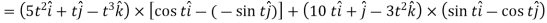
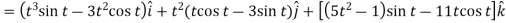
Q2) If 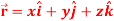, then show that

1.

2.

A2)

Suppose 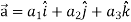  and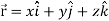

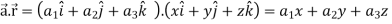
Now taking L.H.S,

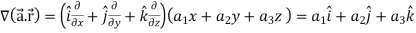
Which is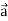

Hence proved.

2.

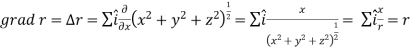
So that

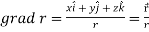
Q3) If 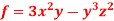then find grad f at the point (1,-2,-1).

A3)

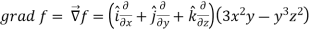
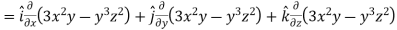
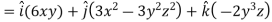
Now grad f at (1 , -2, -1) will be-       

Q4) If 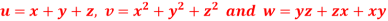then prove that grad u , grad v and grad w are coplanar.

A4)

Here-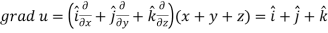                     

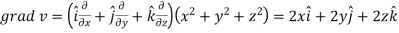
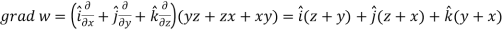
Now-

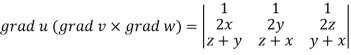
Apply

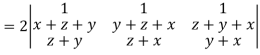
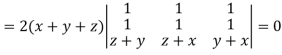
Which becomes zero.

So that we can say that grad u, grad v and grad w are coplanar vectors.

Q5) Show that-

1.

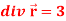
2.

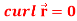
A5) We know that-

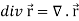
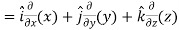
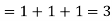
2. We know that-

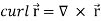
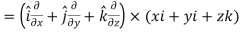
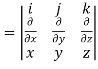
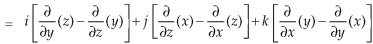
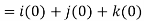= 0

Q6) Prove that

Note- here is a constant vector and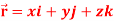

A6) here    and

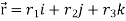
So that

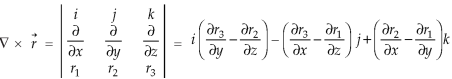
Now-

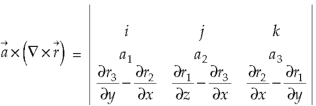
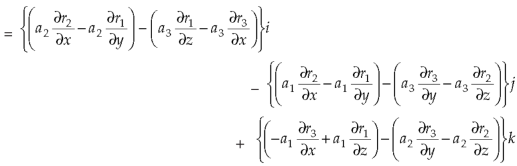
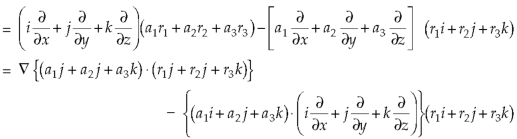
So that-

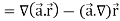
Q7) What is the curl of the vector field F= ( x +y +z ,x-y-z,)?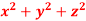

A7)

Curl F =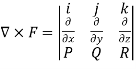

=

=

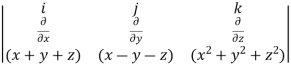
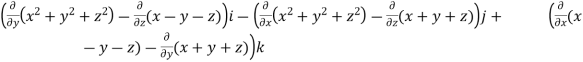
= (2y+1)i-(2x-1)j+(1-1)k

= (2y+1)i+(1-2x)j+0k

= (2y+1, 1-2x,0)

Q8) Find the curl of F = ()i +4zj +

A8)

Curl F=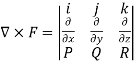

=

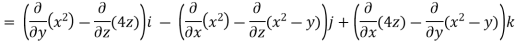
=(0-4)i-(2x-0)j+(0+1)k

=(-4)i – (2x)j+1k

=(-4,-2x,1)

Q9) Find the directional derivatives of at the point P(1, 1, 1) in the direction of the line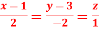

A9) Here

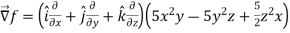
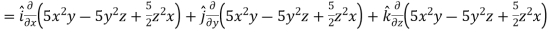
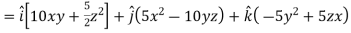
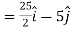
Direction ratio of the line 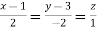are 2, -2, 1

Now directions cosines of the line are-

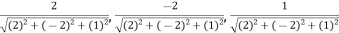
Which are

Directional derivative in the direction of the line-

Q10) Prove that the vector field 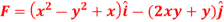is irrotational and find its scalar potential.

A10) As we know that if 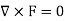then field is irrotational.

So that-

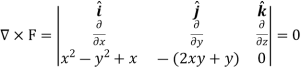
So that the field is irrotational and the vector F can be expressed as the gradient of a scalar potential,

That means-

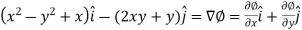
Now-

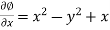   ………………… (1)

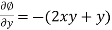  ……………………. (2)

Integrating (1) with respect to x, keep ‘y’ as constant-

We get-

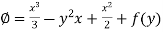      …………….. (3)

Integrating (1) with respect to y, keep ‘x’ as constant-

We get-

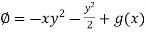      …………….. (4)

Equating (3) and (4)-

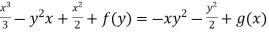
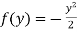  and 

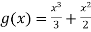
So that-

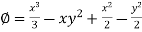
Q11) Show that the vector field 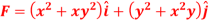is irrotational and find the scalar potential function.

A11) Now for irrotational field we need prove-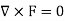 

So that-

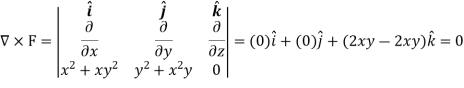
So that the vector field is irrotational.

Now in order to find the scalar potential function-

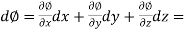
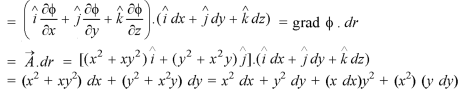
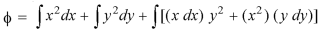
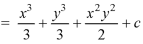
Q12) Evaluat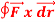e where = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).

A12)  F x dr =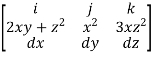

Put x=t, y=t2, z= t3

Dx=dt ,dy=2tdt,                dz=3t2dt.

F x dr =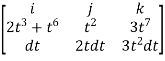

=(3t4-6t8) dt i  – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k

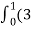=t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k

=

=+

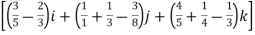
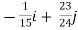Q13) Evaluate 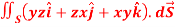, where S is the surface of the sphere in the first octant.

A13) Here-

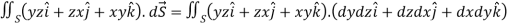
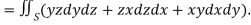
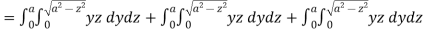
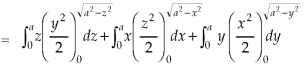
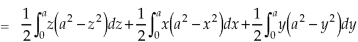
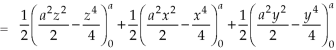
Which becomes-

Q14) Evaluate 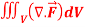if V is the region in the first octant bounded by 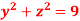and the plane x = 2 and .

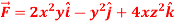A14)

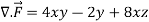
x varies from 0 to 2

The volume will be-

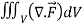
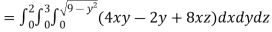
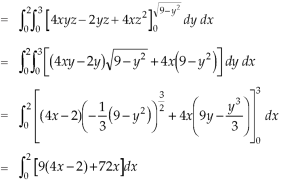
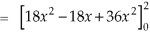
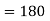
Q15) Apply Green’s theorem to evaluate 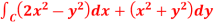where C is the boundary of the area enclosed by the x-axis and the upper half of circle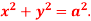

A15) We know that by Green’s theorem-

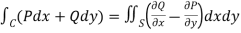
And it it given that-

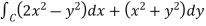
Now comparing the given integral-

P = 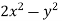  and   Q =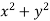

Now-

  and

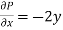
So that by Green’s theorem, we have the following integral-

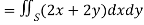
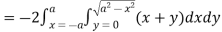
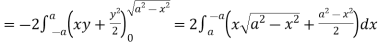
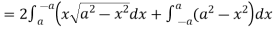
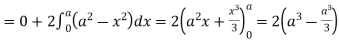
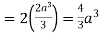
Q16) Verify green’s theorem in xy-plane for 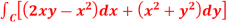where C is the boundary of the region enclosed by

A16)

On comparing with green’s theorem,

We get-

P = and Q =

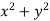
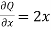  and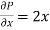

By using Green’s theorem-

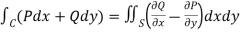  ………….. (1)

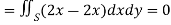
And left hand side=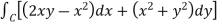

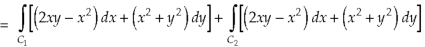………….. (2)

Now,

Along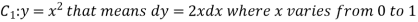

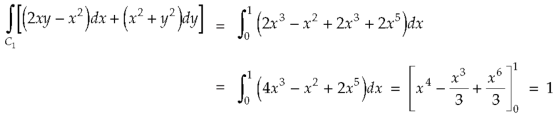
Along

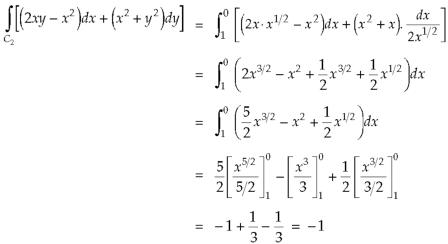
Put these values in (2), we get-

L.H.S. = 1 – 1 = 0

So that the Green’s theorem is verified.

Q17) 2 Show that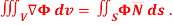 

A17)

By divergence theorem, 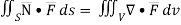..…(1)

Comparing  this  with  the  given  problem  let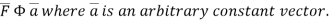 

Hence, by (1)

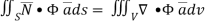                                    ………….(2)

Now ,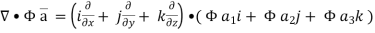  

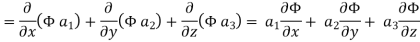
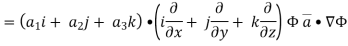
Hence, from (2), We get,

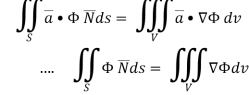
Q18) Verify stoke’s theorem when 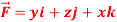and surface S is the part of sphere 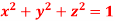, above the xy-plane.

A18)

We know that by stoke’s theorem,

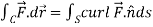
Here C is the unit circle-

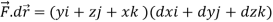
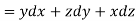
So that-

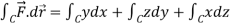
Now again on the unit circle C, z = 0

Dz = 0

Suppose,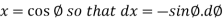 

And           

Now

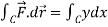
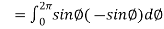
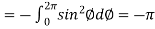  ……………… (1)

Now-

Curl

Using spherical polar coordinates-

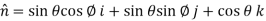
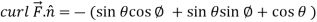
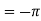  ………………… (2)

From equation (1) and (2), stoke’s theorem is verified.