Unit 3
DC Machines (Part–1)
Q.1) Give detailed description of generating and motoring mode of DC machine.
Sol:
Generating Action:
The basic circuit model for a dc machine is shown below:
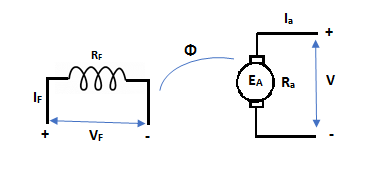
The machine operates in generating mode when the armature current is in the direction of induced emf Ea.
V = Ea – Ia Ra Ea> V
Pmech = Ea Ra = Pelect
The output power,
P0 = VIa
EaIa – VIa = Ia2 Ra
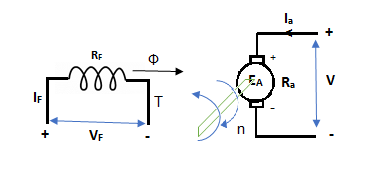
In this mode, the torque of electromagnetic origin is in opposite direction of rotation of armature.
[Pmech]gross = Shaft power = [Pmech]net + Rotational loss.
Motoring Action
In this mode, the armature current Ia flows opposite to the emf induced i.e. Ea. The basic circuit showing this mode is below:
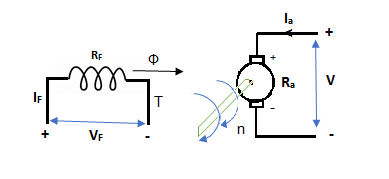
(Ea – Eb) is called as back emf here as it opposes the armature emf.
V = Ea + IaRa
Electrical power connected to mechanical form
Pelec / net = EaIa
Power input, Pi = V Ia
V Ia – EaIa = Ia2Ra = armature copper loss.
The back emf is given as
Eb =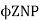 
Q.2) Explain types of DC motor
Sol: Shunt motor – In this, the field winding is connected in parallel with the armature.
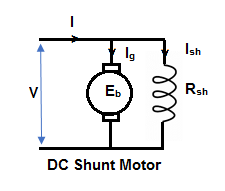
The input current I = Ia + Ish
For field winding, V = IshRsh
For armature, V = Eb + IaRa
Ia = armature current
Ish = shunt field current
V = input voltage
I = Input current
Power Input = Mechanical power + losses in armature + losses in field
VI = Pmech + Ia2Ra + Ish2Rsh
Pmech = VI – VIsh - = Ia2Ra
= V(I – Ish) – Ia2Ra
= VIa - = Ia2Rsh = (V – IaRa)Ia
Pmech = EaIa
1) Series motor – In this, the field winding is connected in series with the armature.
Ise = series field current
I = Ia = Ise
V = Ea + I(Ra + Rse)
VI = EaI + I2(Ra + Rse)
VI = Pmech + I2 Ra + I2Rse
Pmech = Ea I
2) Compound Motor – It is a type of dc motor which had both shunt and series field windings.
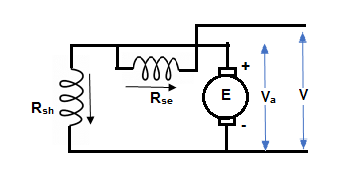
V = Ea ± Ia (Ra + Rse)
IL = Ia ± IF
They are basically of 2 types- long shunt and short shunt.
Q.3) Derive Torque equations of DC machine.
Sol: Motor Torque
1) Armature Torque (Ta) of motor –
Power developed = Ta × 2πN W
As electrical power is converted to mechanical =EbIb
So, power developed = Power converted
Ta × 2πN = EbIb
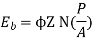
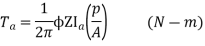
We can also conclude from the above eqn.
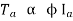
For series,
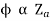
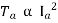
For shunt,
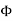is constant practically.
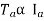
2) Shaft Torque (Tsh) –
The torque doing useful work is called as shaft torque, Tsh.
Motor output =Tsh × 2πN
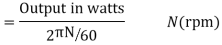
Due to iron and friction losses in motor Ta – Tsh difference torque exists called as lost torque.
Q.4) An 8 pole DC shunt generator with 730 wave connected armature conductor s and running at 500 rpm supplies a load of 11.5Ω resistance at terminal voltage of 250v. The armature resistance is 0.3Ω and field resistance of 235Ω. Find armature current and induced emf.
Sol: Load current = V/R = 250/11.5 =21.74A
Shunt current = 250/235 =1.064A
Armature current = 21.74+1.064 = 22.8A
Induced emf = 250 + (22.84 x 0.3) = 256.8V
Q.5) A short shunt DC compound generator supplies 210 A at 100v the resistance of armature, series field and shunt field windings are 0.05Ω, 0.03Ω and 50Ω respectively. Find EMF generated.
Sol: For short shunt connection armature terminal voltage Va = 100+ (210x0.03) =106.3V
Shunt field current = 106.3/50 = 2.13A
Armature current =210+2.13 =212.13A
Induced emf = 106.30 + (212.13 x 0.05) = 116.9V
Q.6) The armature of a four pole DC shunt generator is lap wound and generates 210v when running at 500 rpm. Armature has 132 slots, with 6 conductors/slot. If armature is rewound, wave connected, find EMF generated with same flux/pole running at 300rpm.
Sol: Total conductors Z = 132x6= 792
The emf E=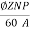 
For lap winding P=A
E=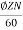 
210=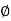
x 792 x 500/60
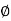= 31.82mWb
If wave connected number of parallel paths = 2
The emf E=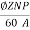 
= (31.82x10-3 x 792 x 300/60) (4/2)
E= 252V
Q.7) A 15kW 400V 350rpm dc shunt motor has current 30A at full load. The moment of inertia of rotating system is 6.5kg-m2. The starting current be 1.2 times of full load current. Find the full load torque?
Sol: Full load output = 15000W
Speed N=350rpm=5.83rps
Output = Tω
T = 15000/2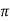
x5.83 = 409.3N-m
Q.8) A DC series motor operates at 600 rpm with line current of 110A from 220v main. It’s armature resistance is 0.2Ω and field resistance is 0.1ohm Find the speed at which motor runs at a line current of 25A, given flux at this current is 45% of flux at 110A.
Sol: 
= 0.45 
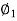
E1=220 – (0.2+0.1) x 110=187V
E2=220 – (0.2+0.1) x 25 = 212.5V
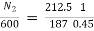
N2= 1515.15rpm
Q.9) A belt driven,120kWshunt generator running at 310 rpm on 220v busbars continues to run as a motor when the belt breaks, then taking 10kW. What will be its speed with armature resistance of 0.03 Ω field resistance of 60Ω and contact drop under each brush is 1v.
Sol: Input current = 120x1000/220 = 545.45A
Shunt current Ish= 220/60 = 3.67A
Armature current Ia= 545.5-3.67=541.83A
E2= 220 – (541.83 x 0.03)- 2x1[drop across brush]
E2=205.74V
The armature current Ia now becomes Ia= 545.5+3.67= 549.17A
As the system here runs as a generator.
E1= 220 – (549.17 x 0.03) +1x2 = 201.5V
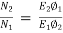
As shunt current is constant so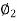 
= 
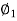
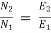
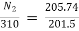
N2= 316.5rpm
Q.10) The input to 230v DC shunt motor is 12kW. Calculate the torque developed, efficiency. No load current=6A, No load speed=1200rpm armature resistance=0.5Ω, shunt field resistance= 110Ω.
Sol: No load input =230x6=1380W
Ish=230/110 =2.1A
Armature current at no load = 6-2.1 = 3.9A
No load armature Cu loss= 3.92 x 0.5= 7.6W
Constant losses = 1380 – 7.6 = 1372.4W
When input is 12kW
Input current = 12000/230 = 52.17A
Armature current = 52.17 – 2.1=50.07A
Armature Cu loss = 50.072 x 0.5 =1253.69W
Total loss=1253.69+1372.4=2626.09W
Output= 12000-2626.09 =9373.9W
Efficiency = 9373.9/12000=0.781=78.1%
Q.11) A 230v DC series motor is running at a speed of 550rpm and draws 50A. Calculate at what speed the motor will run when developing half the torque. Total resistance of armature and field is 0.08Ω.
Sol: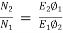 
=
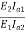
Ta α φIa
Ta α 
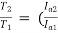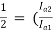)2
)2
Ia2 = 50x0.707=35.35A
E1=230- (50x0.08) =226V
E2=230- (35.35x0.08) =227.17V
=
=
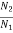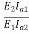
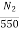N2= 781.97rpm
Q.12) A 230v shunt motor has an armature resistance of 0.3Ω and field resistance of 140Ω. The motor draws 5A at 1600rpm at no load. Calculate the speed of motor?
Sol: Ish= 230/140= 1.643A
Ia1=5-1.643=3.36A
Ia2=50-1.643=48.36A
E1= 230- (3.36x0.3) =226.34V
E2= 230- (48.36x0.3) =215.5V
=
=
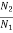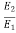
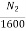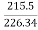
N2= 1523.37rpm
Q.13) A DC series motor drives a load, the torque if which varies as the square of the speed. Assuming magnetic circuit to remain unsaturated and negligible motor resistance. Calculate the reduction in motor terminal voltage which will reduce the motor speed half the value it has on full load.
Sol: Ta α φIa
Ta α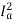 
Ta α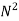 
N2 α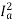 
=
=
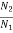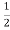
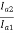Let V1 and V2 be voltage across motor in two cases.
E1=V1 and E2=V2
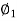αIa1
=
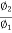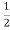
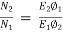
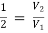x 2
= 
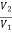% reduction in voltage = V1-V2/V1 x 100 = 4-1/4 x100 = 75%
% change in motor current = Ia1-Ia2/Ia1 x 100 = 50%
Q14) A 10kW 400V 350rpm dc shunt motor has current 30A at full load. The moment of inertia of rotating system is 6.5kg-m2. The starting current be 1.2 times of full load current. Find the full load torque?
Sol: Full load output = 10000W
Speed N=350rpm=5.83rps
Output = Tω
T = 10000/2
x5.83 = 272.99N-m
