Unit - 3
Transients in RLC circuit
Q1) For the circuit given below Find V0 (t) for t =o if the capacitor is uncharged?

A1) Finding Req
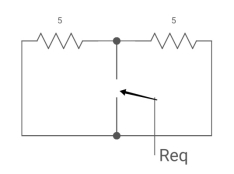
Fig Circuit for Req
Req = R1R2 /R1+R2
V0(0)=0
V0 (infinity) = VR R2/R1+R2
V0 (t) = V0 (infinity) + [Vo (0) – V0 (infinity)] e-t/c
=VR R2/R1+R2 *[ 1- e+(R1+R2)/R1R2]
Q2) Find the value of V0(t) for the circuit below?
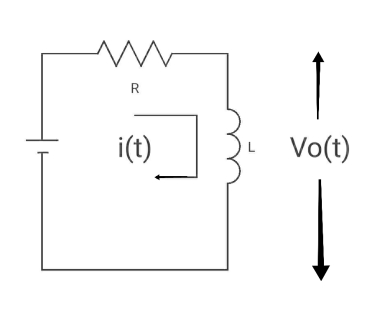
A2) Time constant, c= L/Req = L/R
V(infinity) = 0
V(0) = VR
I(infinity) = VR/R, I (0) =0
By KVL,
VR=i(t) R + L di/dt(t)
On solving
V0(t)= VR e-tR/L
Q3) Find i(t) for the circuit below for t>0?

A3) The circuit for Req will be
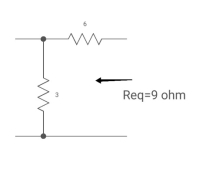
Fig Circuit for Req
Req = 6+3
= 9ohm
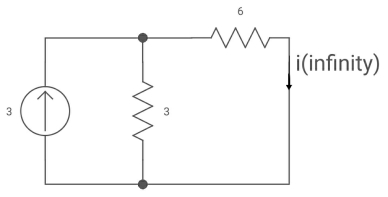
Fig Circuit when inductor acts as short circuit
T= L/Req = 2/9 sec
I(0) =0
I(infinity) = 3*3/6+3 = 1A
i(+) = 1 [1-e4.51]
Q4) Capacitor is initially uncharged find Vc (t); t >0
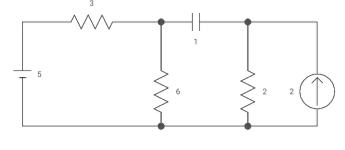
A4)

Fig Circuit for Req
Req = (3116)+2
=2+2 = 4ohm
C= c Req
= 2 sec
Clearly Vc(0) =0
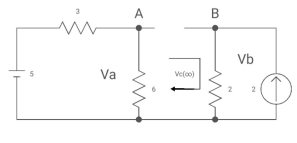
Fig Circuit when the capacitor acts as an open circuit
By voltage divides, VA = 5*6/3+B = 30 v/9
Clearly by ohms low
VB = 2*2 = 4v
Apply KVL, VA-Vc-VB =0
Vc(infinity) = 30/9 – 4 = -2/3 V
Vc (t) = -2/3 [1- e0.5t]
CURVE:-
Vc(t) =2/3 [1-e-0.5t]
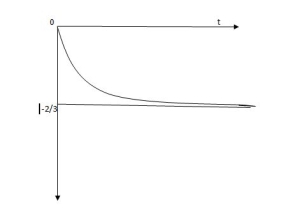
Fig Response for the above circuit
Vc(t) = -2/3 [1-e-0.5t]
Q5) Find i(t) for the given circuit below?

A5) We know i(t) = I (infinity) +[i(0)- i(infinity)] e-t/c
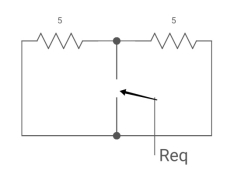
Fig Circuit for Req
Req = 5*5/5+5 = 5?2 ohm
:. T=L/Req = 4/5 sec
Also, i( 0) =0
i(infinity) = u(t) +2/5 u(t)
:. I(t) = 1.4 [1-e-5/4t)]u(t)
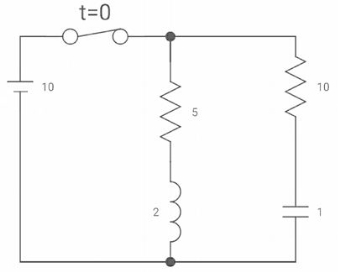
Q6) If switch ‘s’ closed at t= 0 find out the voltage across the capacitor and current through capacitor at t= 0+?
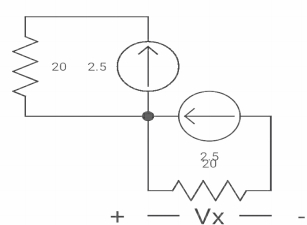
A6) At t= 0- the switch was open so,
:. There is no powntial so Vc(0-) = 0
At t= 0+, Vc (0-) = Vc(0+) = 0

Isc = 10/5 = 2 A
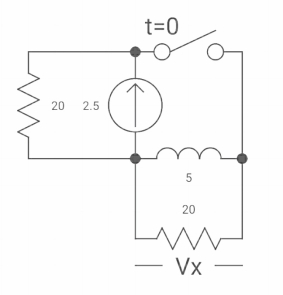
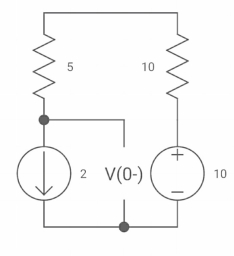
Q7) The switch was closed for a long time before Opening at t=0- find VX (0+)?
(a) 25V (b) 50 V (c)-50V (d) 0V
A7) At time t=0-
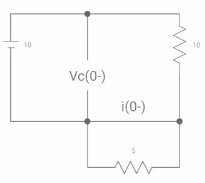
clearly, il(0-) = 2.5 A
at t= 0+ , as inductor is initially charges
so il (0-) = il(0+)
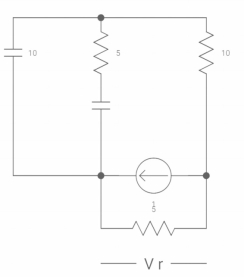
-VX= 20/2.5 20*2.5
VX= -50A
Q8) Find VR(0+) and dil/dt(t) = 0+ If switch is opened at t= 0?

A8)
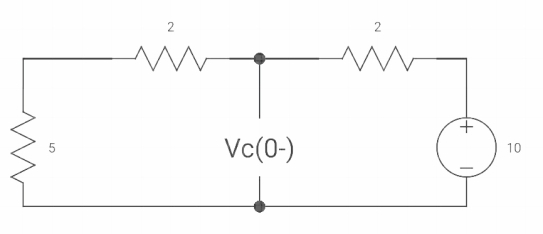
At t=0-
Vc(0-) = 10V
IL(0-) = 10/10 = 1 A
Also, iL(0-) = iL(0+) = 1A
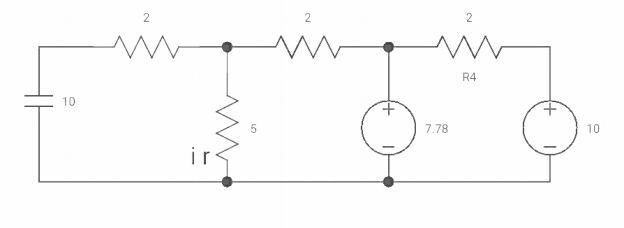
VR(0+) = 5V
Ldi(t)/dt = VL (t)
DiL(t)/dt = VL(t)/L
At t= 0+
d/dt iL (0+) = VL(0+)/L
-VL (0+)-VR =0
VL (0+) = -5V
dt(t) at t = ot = vl (ot)/L
=-5/2
dil/dt(o+) = 2.5 A/s
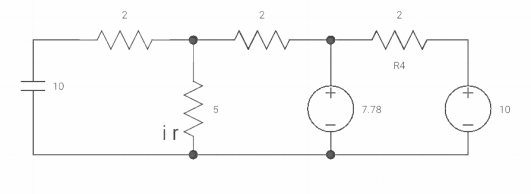
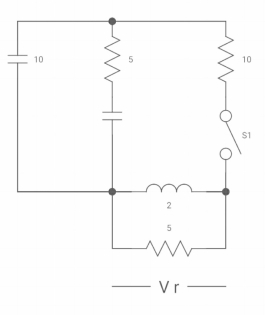
Vc(o+) and iR (o+) it switch ‘s’ is closed at t=0?
At t=0
As the capacitor is fully charged so acts as
Vc (0-) = 7*10/7+2 = 70/9v
At t=0+
Vc(0+) = Vc (0) = 40/9v
By applying kcl at A,
VA-10/2+ VA/5+VA-7019/2 =0
VA [1/5+!/2+1/2] = 5+35/9
Va [6/5] = 80/9
Va= 400/54v
IR (0+) = va/5 = 400/54*5 = 80/54 A
Q9) Derive the time constant for the RC circuit?
A9) FOR RC Circuit

Fig 2: Series RC circuit
 =V
=V
For t>0 applying KVL
Ri(t)+ +V=0
+V=0
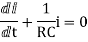
Hence the general solution of the above equation is calculated the same as for the RL circuit
i=k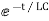
i(0)=- 
Hence, a particular solution for the network is given as
i=- 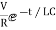 tfor t≥0
tfor t≥0
=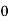 for t<0
for t<0
The time constant is given as 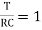
T=RC
Q10) Write the equation for the complete solution of a differential equation?
A10) The complete or total response of the network is the sum of the transient response and steady-state response which is represented by the general solution of the differential equation.
First-order homogenous differential equation.
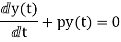
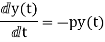
Integrating both sides
y(t)=k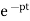
First-order non-homogenous differential equation

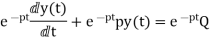
Integrating the above equation, we get
y(t)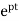 =∫ Q
=∫ Q 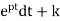
y(t)=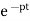 ∫ Q
∫ Q 
The first term of the above solution is known as particular Integral and the second is known as a complementary function.