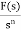Unit - 4
Laplace Transform
Q1) Find the initial value for the function f(t) = 2u(t)+3cost u(t)?
A1) f(t) = 2u(t)+3cost u(t)
F(s) =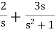 
sF(s) = 2+ 
By initial value theorem
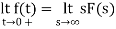= f(0+)
= 
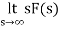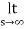2+ 
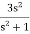= 5 = f(0+)
Hence, the initial value of the function is 5
Q2) Find the final value of the function F(s) =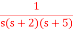 
A2) F(s) =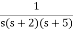 
sF(s) =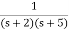 
By final value theorem
= 
= 
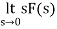= 0.1
So, the final value of the function is 0.1
Q3) Write an equation for a given waveform
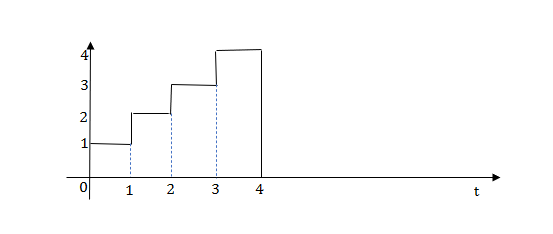
A3)
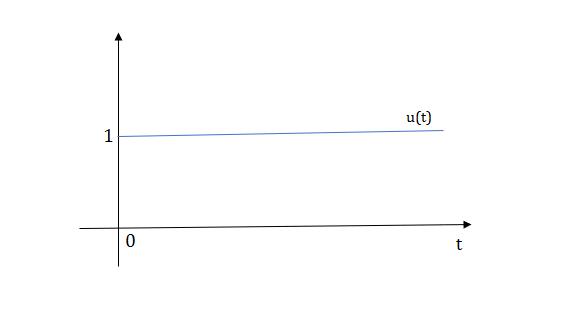
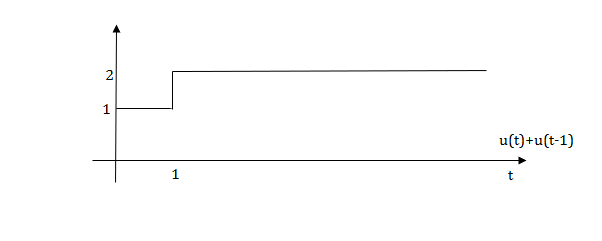
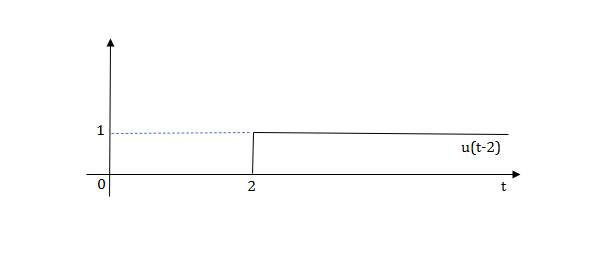
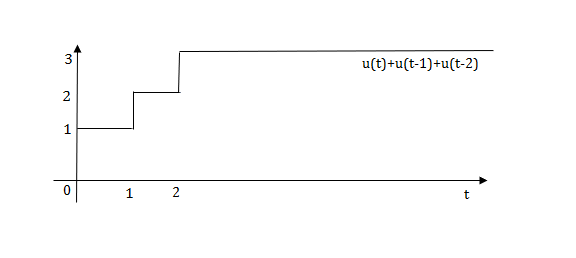
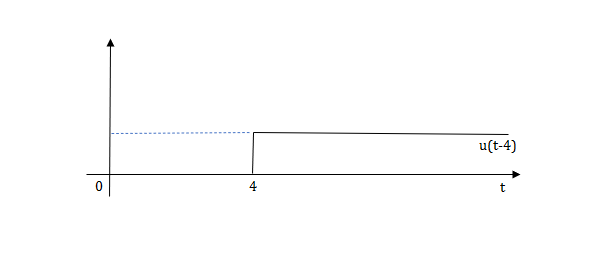
The final equation is=u(t)+u(t-1)+u(t-2)+u(t-3)-4u(t-4)
As the waveform is stopped at t=4 with amplitude 4, so we have to balance that using -4u(t-4).
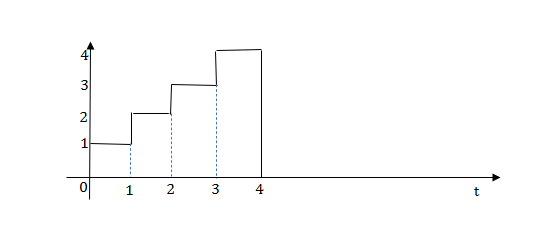
Q4) Write the equation for the given waveform.
A4) Calculating the slope of the above waveform
Slope for (0,0) and (1,2)
a1 slope=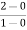
=2
a2 slope=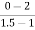
=-4
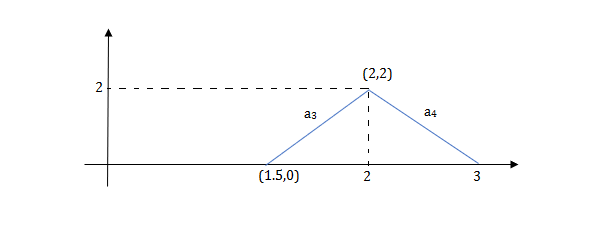
a3 slope =4 and a4= -2
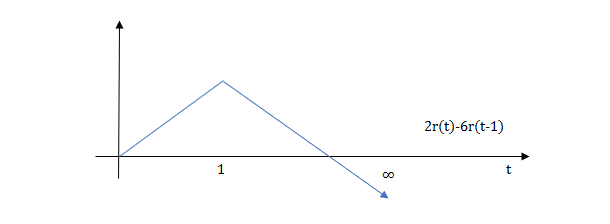
At t=1 slope changes from 2 to -4 so we need to add -6r(t-1) to 2r(t) to get the slope of -4.
At t=1.5 slope changes from -4 to 4 so adding 8r(t-1.5) to get slope of 4
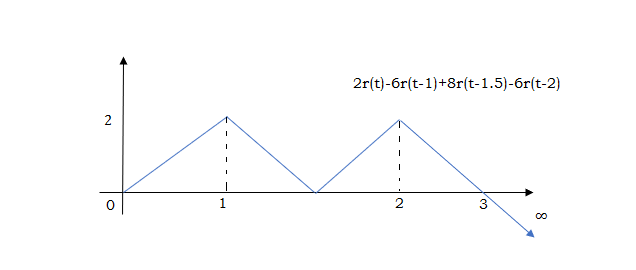
At t=2 slope changes from +4 to -2 so we add -6r(t-2). But we need to stop the waveform at t=3. Hence we have to make slope 0. Which can be done by adding +2r(t-3). Final equation is given as
2r(t)-6r(t-1.5)+8r(t-1.5)-6r(t-2)+2r(t-3)
Q5) The switch is at before moving to position = at t= 0, at t= 0+, i1(t) is
(a) –V/2R (b) –V/R (c) – V/4R (d) 0
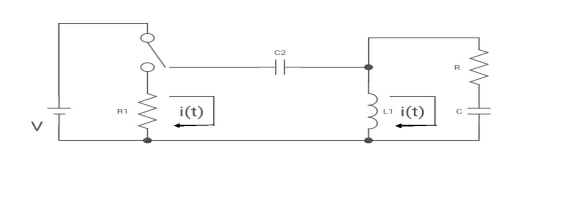
A5) I1(t) L.T I1(s)
I2(t) L.T I2(s)
then express in form
[ I1(s)/I2(s)] [::] .[:]
Drawing the ckl at t = 0-
Diagram
:. The capacitor is connected for long
Vc1(0-)= V
iL(0-) =0
Vc2(0-)=0
at t= 0+
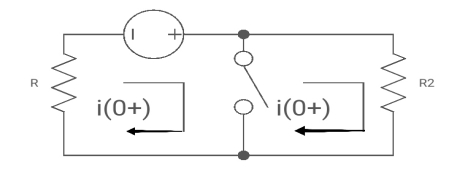
i1 (0+) = -V/2R
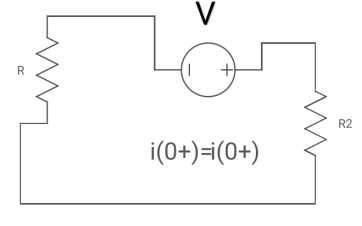
for t>0 the circuit is
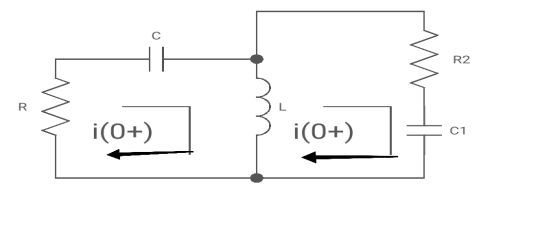
Apply KVL
-R i1(t) -1/c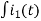 
dt -L
=0
Also, we can deduce i1(t)- i2 (t) = iL(t)
-Ri1(t) -1/c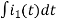 
- L
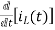= 0
-RI1(s)-[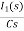
-
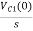]-L[sI1(s)-iL(0-)]=0
- RI1(s)-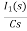
- 
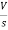-s L I2(s)=0
- s L I2(s)= - 
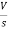(1)
Again
-Ri2(t) ) -1/c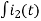 
dt -L
=0
-Ri1(t) -1/c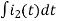 
- L
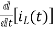= 0
Taking Laplace Transform
-RI2(s)- [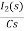
-
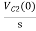]- L[s IL(s)- iL(0-)]=0
-RI2(s)-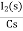 
-
Ls[ I1(s)- I2(s)]=0
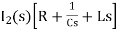- s L I1(s)=0 (2)
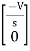
Hence in the matrix representation
= 
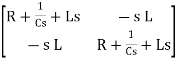
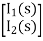Q6) All initial conditions are zero i(t) I(s), then find I(s)?
A6) Drawing Laplace circuit
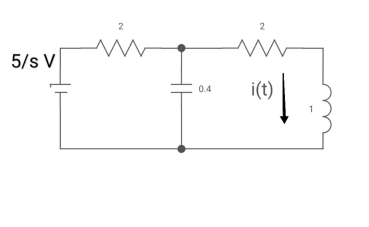
(2+S) 11 2/S
Zeq = [(2+S)2/S]/[2+S+2/S]=[2(S+2)]/[S2+2s+2]
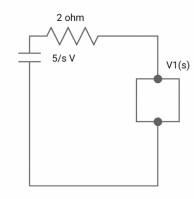
V1(s) = [5/S{2(S+2)/S2+2S+2}]/[2+{2(S+2)/ S2+2S+2}]
V1(s) = [5(S+2)/S]/[S2+ 3S +4]
I(s) = V1(s)/(S+2) = (5/S)/(S2+35+4)
Q7) Find IL(0)
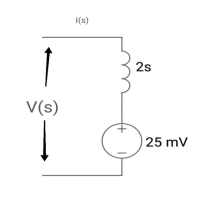
A7) From the above circuit
L = 2H
LiL (0) = 25 mv
IL (0) = 12.5 m A
Q8) Find value across the capacitor?
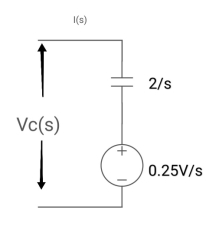
A8) From above circuit we can write
1/cs = 2/s
C=1/2f
Vc (0)/s = 0.25v/s
Vc(0)= .25v
Q9) Find the voltage across the capacitor?
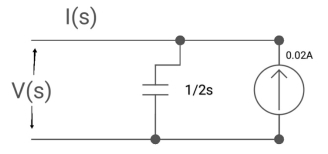
A9) 1/cs = 1/2S
C=2F
CVc (0) = 0.02
Vc(0)= 0.01V
Q10) List the properties of the Laplace transform.
A10) Properties of Laplace Transform:
1) Linearity Property:
If f1(t) and f2(t) are two functions of time. Then, in the domain of convergence
L[a f1(t)+b f2(t)]=a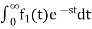
+ b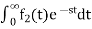
=aF1(s)+bF2(s)
2) Differentiation Property:
If x(t) is a function of time then Laplace transform of the nth derivative is given as
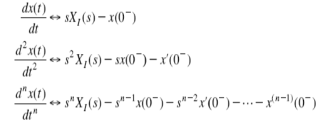
3) Integration Property:
The Laplace of nth order integral is given as
L[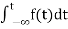
]=
+
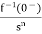
L[f-n(t)]=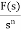
+
+
+……….
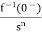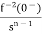As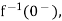 
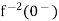……..=0.
Hence
L[f-n(t)]=
