Q1) Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].

A1) As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).

f(x) = (x-1)(x-2)(x-3)

f(x) =  x-6x²+11x-6

Now at x = 0, we get

f(0) = -6  and

At x = 4, we get.

f(4) = 6

Diff. The function w.r.t.x , we get

f’(x) = 3x²-6x+11

Suppose x = c, we get

f’(c) = 3c²-6c+11

By Lagrange’s mean value theorem,

f’(c) = 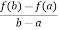   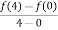 =  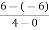   =   = 3

Now we get,

3c²-6c+11 = 3

3c²-6c+8 = 0

On solving the quadratic equation, we get

C = 2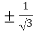

Here we see that the value of c lies between 0 and 4

Therefore the given function is verified.

Q2) Define the floating-point form.

A2)

Let x be a non-zero real number. An n-digit floating-point number in base 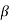has the form-

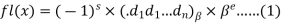
Where

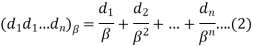
Is a 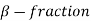called mantissa,

s = 0 or 1 called the sign, and e is an integer called the exponent.

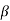is called a radix.

The point preceding 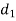in equation (1) is called the radix point.

Q3) Define absolute error and relative error.

A3)

Absolute Error:

The Approximate error is the numerical difference between the quantity of the exact solution and the approximate value of the solution.

Let X   be the exact solution and the approximate value of the solution is denoted by 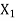, then the absolute error is defined as

Relative  Error:

The error obtained by dividing the approximate solution by the exact solution is known as relative error and is denoted by

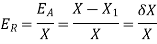
The percentage error is the 100 times of the relative error i.e.

.

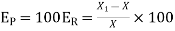The absolute accuracy is magnitude absolute error.

.

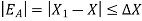The relative accuracy is the magnitude of the relative error.

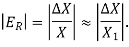
Q4) An approximate value of   is given by 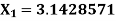and its exact value is 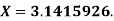Find the absolute and relative errors.

A4)

The absolute error is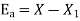

.

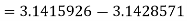
The relative error is

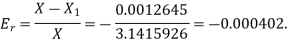
Q5) Round –off the following number to two decimal places

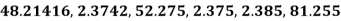
A5)

Q6) Find a real root of 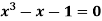using bisection method correct to five decimal places.

A6)

Let then by hit and trial we have

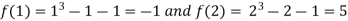
Thus 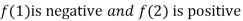. So the root of the given equation should lie between 1 and 2.

Now,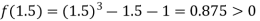

i.e. positive so the root of the given equation must lie between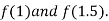

Now,

i.e. negative so the root of the given equation lies between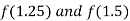

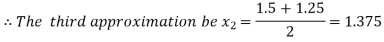
Now,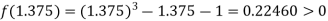

i.e. positive so the root of the given equation lies between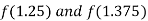

Now,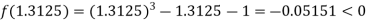

i.e. negative  so that the root of the given equation lies between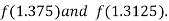

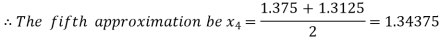
Now,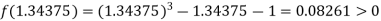

i.e. positive so that the root of the given equation lies between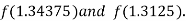

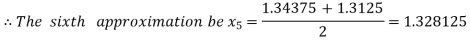
Now,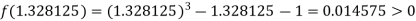

i.e. positive so that the root of the given equation lies between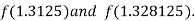

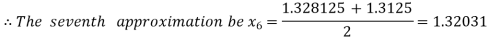
Now,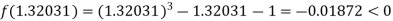

I.e. negative so that the root of the given equation lies between

Now,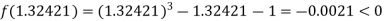

i.e. negative so that the root of the given equation lies between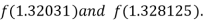

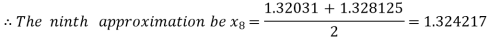
Hence the approximate root of the given equation is 1.32421

Q7) Define Descartes’ rule of the sign.

A7)

According to this rule- A polynomial equation p(x) =, 0 can not have more positive roots than the number of changes in sign of its coefficients.

Similarly, p(x) = 0 cannot have more negative roots than the number of changes in sign of the coefficient of p(x).

Q8) Let us consider a polynomial equation-

A8)

Now going from left to right there are changes between 1 and -15, between -15 and 7, and between 7 and -11.

The total number of changes is 3 and hence it can have the most 3 positive roots.

Now consider-

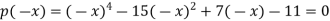
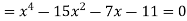
There is one change only between 1 and -15 hence the equation cannot have more than one negative root.

Q9) Find all the roots of polynomial equation 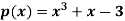rounded off to three decimal places.

[Stop the iteration if |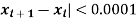

A9)

The equation has three roots.

As there is only one change in the sign of the coefficient, by Descartes’ rule of sign the equation can have at most one positive real root.

The equation has no negative real roots since p(-x) = 0 has no change of sign of coefficients.

Here p(x) = 0  is of one degree, it has at least one real root.

So that the given equation has one positive real root and a complex pair.

Now let's find the real roots by Birge-Vieta method-

The initial iteration is-

So that-

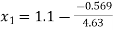= 1.22289

Similarly

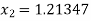
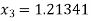
Here we see that 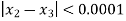so that we stop the iteration.

Hence the value of root is 1.213

Now we get the deflated polynomial of p(x).

In order to obtain a deflated polynomial, we need to find the quadratic equation by using the final approximation.[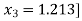

Here we notice p(1.213) = -0.0022,

That is, the magnitude of the error in satisfying p(x) = 0 is 0.0022.

We get-

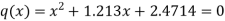
The roots of this quadratic equation are given by-[using quadratic equation]-

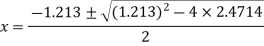
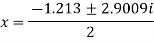
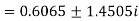
The three roots of the equation rounded off to three decimal places are 1.213, 0.6065+1.4505i  and  -0.6065 - 1.4505i