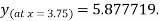Unit - 2
Solution of Transcendental and Polynomial Equation and Curve Fitting
Q1) Find a real root of 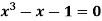 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
A1)
Find a real root of 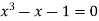 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
Let 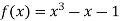 then by hit and trial we have
then by hit and trial we have
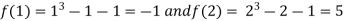
Thus 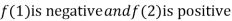 .So the root of the given equation should lies between 1 and 2.
.So the root of the given equation should lies between 1 and 2.

Now, 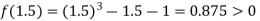
I.e. positive so the root of the given equation must lies between 

Now, 
I.e. negative so the root of the given equation lies between 

Now, 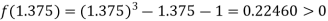
i.e. positive so the root of the given equation lies between 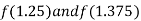
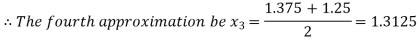
Now, 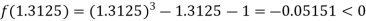
i.e. negative so that the root of the given equation lies between 
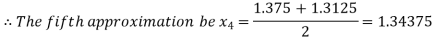
Now, 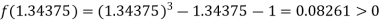
i.e. positive so that the root of the given equation lies between 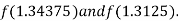

Now, 
i.e. positive so that the root of the given equation lies between 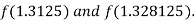
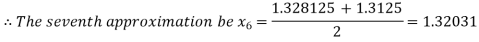
Now, 
i.e. negative so that the root of the given equation lies between 

Now, 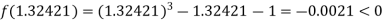
i.e. negative so that the root of the given equation lies between 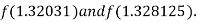
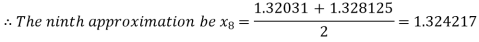
Hence the approximate root of the given equation is 1.32421
Q2) Find the root of the equation 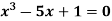 between 2 and 3, using bisection method correct to two decimal places.
between 2 and 3, using bisection method correct to two decimal places.
A2)
Let 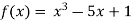
Where 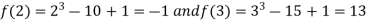
Thus 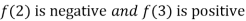 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 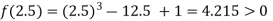
i.e. positive so the root of the given equation must lie between 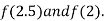

Now, 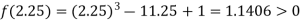
i.e. positive so the root of the given equation must lie between 

Now, 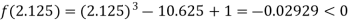
i.e. negative so the root of the given equation must lie between 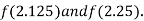
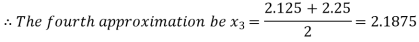
Now, 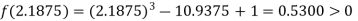
i.e. positive so the root of the given equation must lie between 
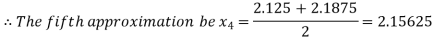
Now, 
i.e. positive so the root of the given equation must lie between 
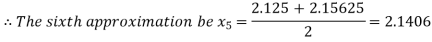
Now, 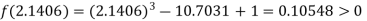
i.e. positive so the root of the given equation must lie between 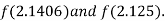
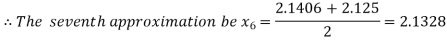
Now, 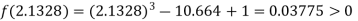
i.e. positive so the root of the given equation must lie between 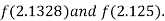

Now, 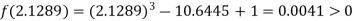
i.e. positive so the root of the given equation must lie between 
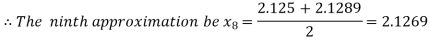
Hence the root of the given equation correct to two decimal places is 2.1269
Q3) Find a real root of the equation 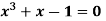 near
near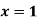 , correct to three decimal places by the Regula Falsi method.
, correct to three decimal places by the Regula Falsi method.
A3)
Let 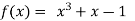
Now, 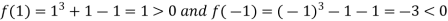
And also 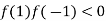
Hence the root of the equation 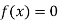 lies between
lies between 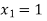 and
and  and so,
and so, 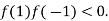
By Regula Falsi Method
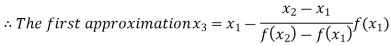
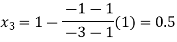
Now, 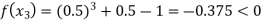
So the root of the equation  lies between 1 and 0.5 and so
lies between 1 and 0.5 and so 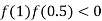
By Regula Falsi Method
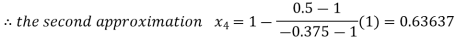
Now, 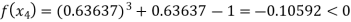
So the root of the equation 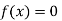 lies between 1 and 0.63637 and so
lies between 1 and 0.63637 and so 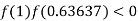
By Regula Falsi Method
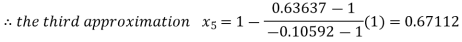
Now, 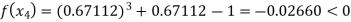
So the root of the equation 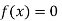 lies between 1 and 0.67112 and so
lies between 1 and 0.67112 and so 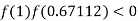
By Regula Falsi Method
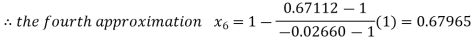
Now, 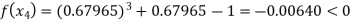
So the root of the equation 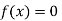 lies between 1 and 0.63636 and so
lies between 1 and 0.63636 and so 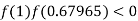
By Regula Falsi Method
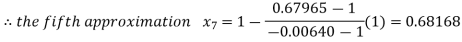
Now, 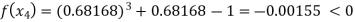
So the root of the equation 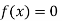 lies between 1 and 0.68168 and so
lies between 1 and 0.68168 and so 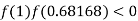
By Regula Falsi Method
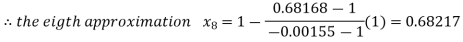
Now, 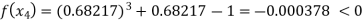
Hence the approximate root of the given equation near to 1 is 0.68217
Example 2 Find the real root of the equation

By the method of false position correct to four decimal places
Let 
By hit and trail method
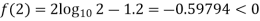
 0.23136 > 0
0.23136 > 0
So, the root of the equation 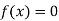 lies between
lies between 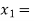 2 and
2 and 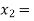 3 and also
3 and also 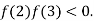
By Regula Falsi Method
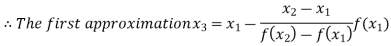
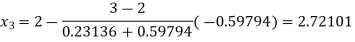
Now, 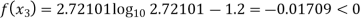
So, root of the equation 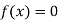 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 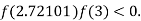
By Regula Falsi Method
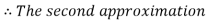
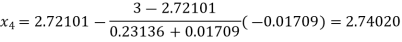
Now, 
So, root of the equation 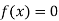 lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 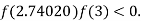
By Regula Falsi Method
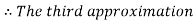
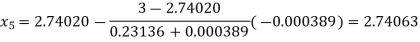
Now, 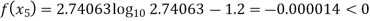
So, root of the equation 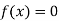 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 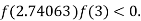
By Regula Falsi Method
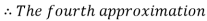

Hence the root of the given equation correct to four decimal places is 2.7406
Q4) Find the real root of the equation
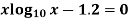
By the method of false position correct to four decimal places
A4)
Let 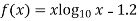
By hit and trail method
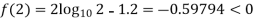
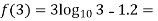 0.23136 > 0
0.23136 > 0
So, the root of the equation 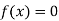 lies between
lies between 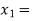 2 and
2 and 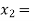 3 and also
3 and also 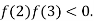
By Regula Falsi Method
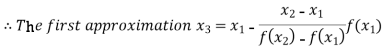

Now, 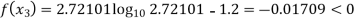
So, root of the equation  lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 
By Regula Falsi Method
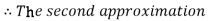
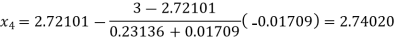
Now, 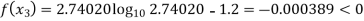
So, root of the equation 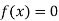 lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 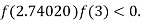
By Regula Falsi Method


Now, 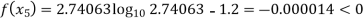
So, root of the equation 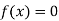 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 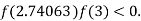
By Regula Falsi Method


Hence the root of the given equation correct to four decimal places is 2.7406
Q5) Apply Regula Falsi Method to solve the equation
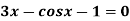
A5)
Let 
By hit and trail
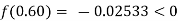
And 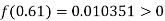
So, the root of the equation lies between 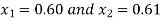 and also
and also 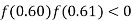
By Regula Falsi Method
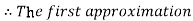
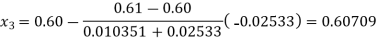
Now, 
So, root of the equation 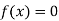 lies between 0.60709 and 0.61 and also
lies between 0.60709 and 0.61 and also 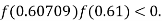
By Regula Falsi Method
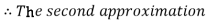

Now, 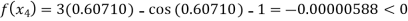
So, root of the equation 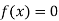 lies between 0.60710 and 0.61 and also
lies between 0.60710 and 0.61 and also 
By Regula Falsi Method
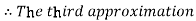
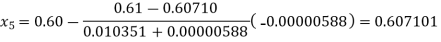
Hence the root of the given equation correct to five decimal places is 0.60710.
Q6) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: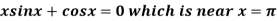
A6)
Given 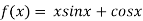
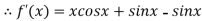
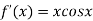
By Newton Raphson Method
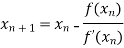
= 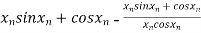
=
The initial approximation is 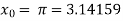 in radian.
in radian.
For n =0, the first approximation 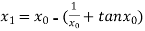

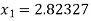
For n =1, the second approximation 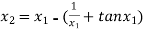
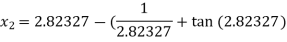
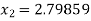
For n =2, the third approximation 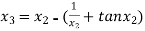
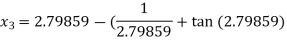
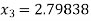
For n =3, the fourth approximation 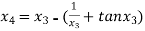
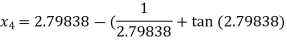
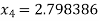
Hence the root of the given equation correct to five decimal places is 2.79838.
Q7) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 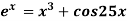 near to 4.5
near to 4.5
A7)
Let 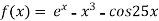

The initial approximation 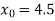
By Newton Raphson Method
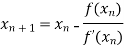
For n =0, the first approximation 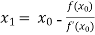
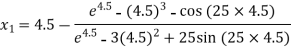
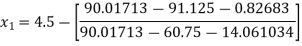

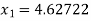
For n =1, the second approximation 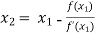
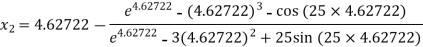
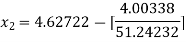
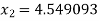
For n =2, the third approximation 
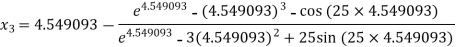
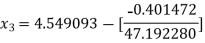
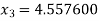
For n =3, the fourth approximation 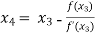
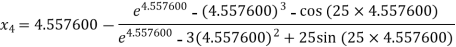
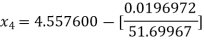
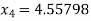
Hence the root of the equation correct to three decimal places is 4.5579
Q8) Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 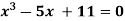
A8)
Let 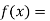
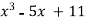
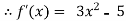
By Newton Raphson Method
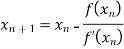
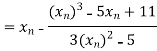
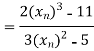
Let the initial approximation be 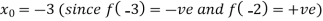
For n=0, the first approximation 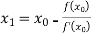
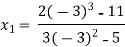
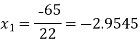
For n=1, the second approximation 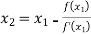
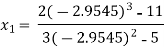
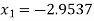
For n=2, the third approximation 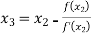
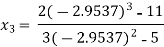
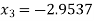
Since 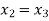 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Q9) Fit a straight line to the following data regarding x as the independent variables:
X | 0 | 1 | 2 | 3 | 4 |
Y | 1 | 1.8 | 3.3 | 4.5 | 6.3 |
A9)
The equation of straight line is
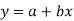
And the normal equations
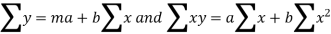
We construct the data table:
X | Y | XY | 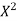 |
0 1 2 3 4 | 1 1.8 3.3 4.5 6.3 | 0 1.8 6.6 13.5 25.2 | 0 1 4 9 16 |
Total 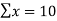 | 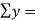 | 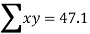 |  |
Here 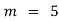 (no. Of steps)
(no. Of steps)
Substituting the values from table in normal equations:
16.9=5a+10b
47.1=10a+30b
On solving we get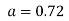 and
and 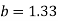
Therefore, the required equation of the straight line is 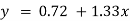 .
.
Q10) Predict y at x = 3.75 by fitting a power curve 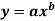 to the given data
to the given data
X | 1 | 2 | 3 | 4 | 5 | 6 |
Y | 2.98 | 4.26 | 5.21 | 6.10 | 6.80 | 7.50 |
A10)
Given equation is 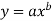
Taking log on both sides,
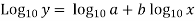
Let 
Therefore, its normal equation is

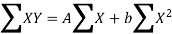
We construct the data table:
 |  | 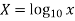 | 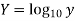 | XY |  |
1 2 3 4 5 6 | 2.98 4.26 5.21 6.10 6.80 7.50 | 0 0.301030 0.477121 0.602060 0.698970 0.778151 | 0.474216 0.629410 0.716838 0.785330 0.832509 0.875061 | 0 0.189471 0.342018 0.472816 0.581899 0.680930 | 0 0.090619 0.227644 0.362476 0.488559 0.605519 |
Total
|
| 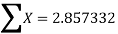 | 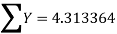 | 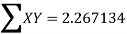 | 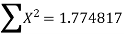 |
Substituting the values from the table in the above equations

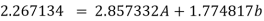
On solving we get 
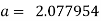
Hence the required equation is 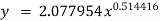
So,