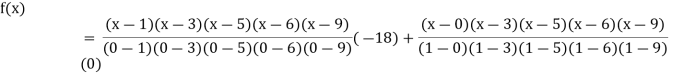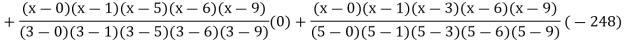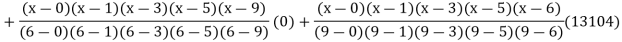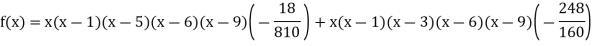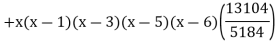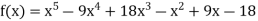Unit - 3
Interpolation
Q1) Using Newton’s forward difference formula, find the sum
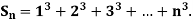
A1)
Putting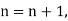 
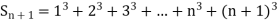
It follows that
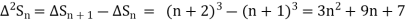
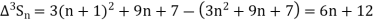
Since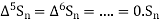 
is a fourth-degree polynomial in n.
Further,
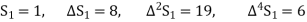
By Newton Forward Difference Method
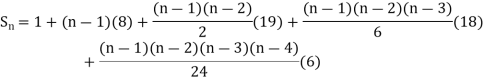
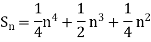
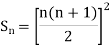
Q2) Given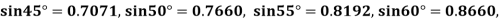 
find 
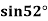, by using Newton forward interpolation method.
A2)
Let 
, then
 |  |  |  |  |  |
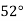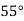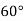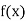 | 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
 |  |  |  |  |
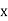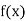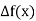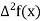45
50
55
60 | 0.7071
0.7660
0.8192
0.8660 |
0.0589
0.0532
0.0468 |
-0.0057
-0.0064 |
-0.0007 |
By Newton forward difference method
Here initial value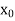 
= 45, difference of interval h = 5 and the value to be calculated at x=52.
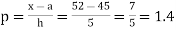
By Formula
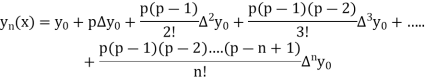
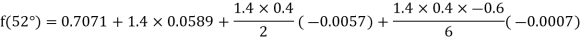
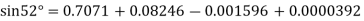
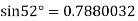
Q3) Find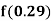 
from the following table:
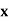 | 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 |
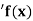 | 1.6596 | 1.6698 | 1.6804 | 1.6912 | 1.7024 | 1.7139 |
A3)
Consider the backward difference method
 |  |  |  |  |  |  |
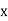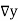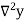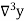0.20
0.22
0.24
0.26
0.28
0.30 | 1.6596
1.6698
1.6804
1.6912
1.7024
1.7139 |
0.0102
0.0106
0.0108
0.0112
0.0115 |
0.0004
0.0002
0.0004
0.0003 |
-0.0002
0.0002
-0.0001 |
0.0004
-0.0003 |
-0.0007 |
Here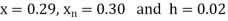 
By Newton backward difference formula
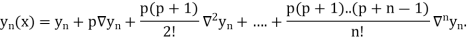
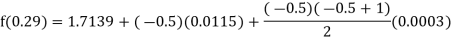
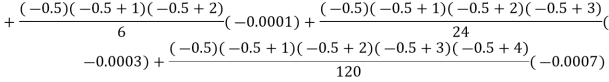
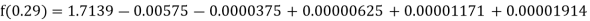
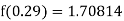
Q4) The following table give the amount of a chemical dissolved in water:
Temp. |  |  |  |  |  |  |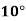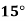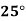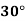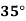
Solubility | 19.97 | 21.51 | 22.47 | 23.52 | 24.65 | 25.89 |
A4)
Compute the amount dissolve at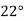 
Consider the following backward difference table:
Temp. x | Solubility y |  |  |  |  |  |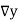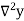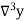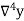
10
15
20
25
30
35 | 19.97
21.51
22.47
23.52
24.65
25.89 |
1.54
0.96
1.05
1.13
1.24 |
-0.58
0.09
0.08
0.11 |
0.67
-0.01
0.03 |
-0.68
0.04 |
0.72 |
Here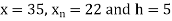 
By Newton Backward difference formula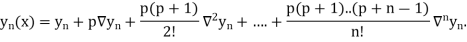
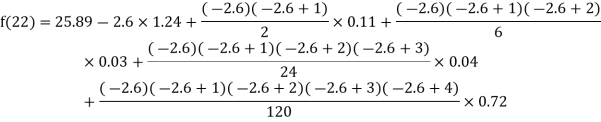
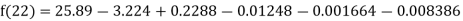
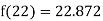
Q5) The following are the marks obtained by 492 candidates in a certain examination
Marks | 0-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 |
No. of candidates | 210 | 43 | 54 | 74 | 32 | 79 |
Find out the number of candidates:
a) Who secured more than 48 but not more than 50 marks?
b) Who secured less than 48 but not less than 45 marks?
A5)
Consider the forward difference table given below:
Marks upto x | No. Of candidates y |  |  |  |  |  |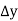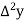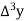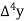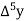
40
45
50
55
60
65 | 210
210+43=253
253+54=307
307+74=381
381+32=413
413+79= 492 |
43
54
74
32
79 |
11
20
-42
47 |
9
-62
89 |
-71
151 |
222 |
Here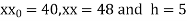 
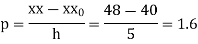
By Newton Forward Difference formula
f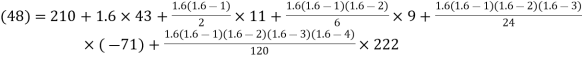
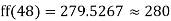
a) No. Of candidate secured more than 48 but not more than 50 marks
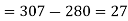
b) No. Of candidate secured less than 48 but not less than 45 marks
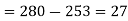
Q6) By using Stirling’s formula to compute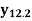 
from the table (
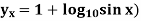given below-
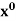 | 10 | 11 | 12 | 13 | 14 |
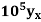 | 23,967 | 28,060 | 31,788 | 35,209 | 38,368 |
A6)
Taking the origin at 
We get the following central table-
P |  |  |  |  |  |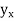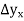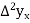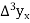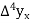
-2
-1
0
1
2 | 0.23967
0.28060
0.31788
0.35209
0.38368 |
0.04093
0.03728
0.034121
0.03159 |
-0.00365
-0.00307
-0.00062 |
0.00058
-0.00045 |
-0.00013
|
At x = 12.2, p = 0.2
Stirling’s formula-
When p = 0.2, we get-
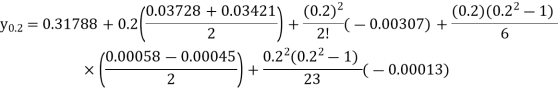
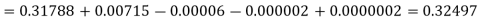
Q7) By using Bessel’s formula to find the value of f(27.5) from the table given below-
x | 25 | 26 | 27 | 28 | 29 | 30 |
f(x) | 4.000 | 3.846 | 3.704 | 3.571 | 3.448 | 3.333 |
A7)
Taking the origin at 
We have p = x – 27
The central table will be as follows-
x | p | y |  |  |  |  |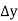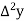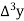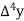
25
26
27
28
29
30 | -2
-1
0
1
2
3 | 4.000
3.846
3.704
3.571
3.448
3.333 |
-0.154
-0.142
-0.133
-0.123
-0.115
|
0.012
0.009
0.010
0.008 |
-0.003
-0.001
-0.002 |
0.004
-0.001 |
At x = 27.5, p =0.5
Bessel’s formula is-
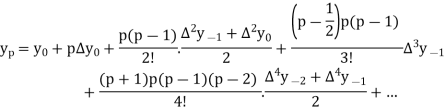
When p = 0.5, we get-
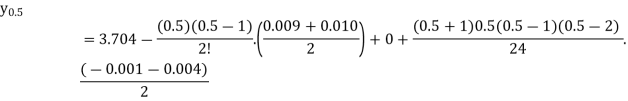
So that-
f(27.5) = 3.585
Q8) By means of Newton’s divided difference formula, find the values of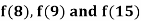 
from the following table:
x | 4 | 5 | 7 | 10 | 11 | 13 |
f(x) | 48 | 100 | 294 | 900 | 1210 | 2028 |
A8)
We construct the divided difference table is given by:
x | f(x) | First order divide difference | Second order divide difference | Third order divide difference | Fourth order divide difference |
4
5
7
10
11
13 | 48
100
294
900
1210
2028 |
 |
 |
 |
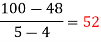
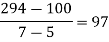
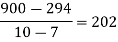
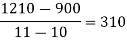
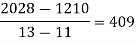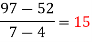
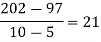
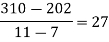
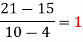
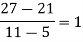
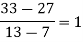0
0 |
By Newton’s Divided difference formula
.
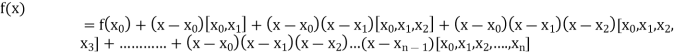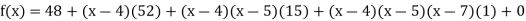
Now, putting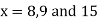 
in above we get
.
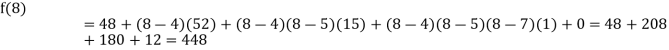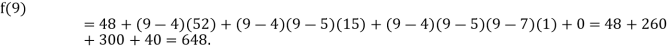
Q9) Find a polynomial satisfied by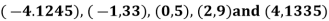 
, by the use of Newton’s interpolation formula with divided difference.
x | -4 | -1 | 0 | 2 | 4 |
F(x) | 1245 | 33 | 5 | 9 | 1335 |
Here
A9)
We will construct the divided difference table:
x | F(x) | First order divided difference | Second order divided difference | Third order divided difference | Fourth order divided difference |
-4
-1
0
2
4 | 1245
33
5
9
1335 |
|
 |
 |
 |
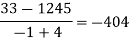
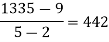
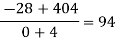
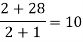
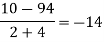
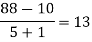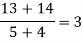By Newton’s divided difference formula
.
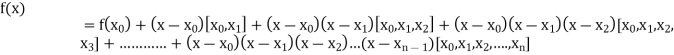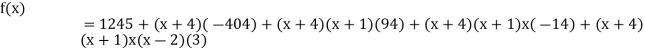
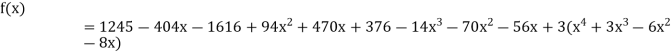
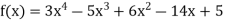
This is the required polynomial.
Q10) find the polynomial of fifth degree from the following data
X | 0 | 1 | 3 | 5 | 6 | 9 |
Y=f(x) | -18 | 0 | 0 | -248 | 0 | 13104 |
Here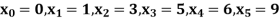 
A10)
We get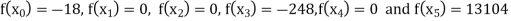 
By Lagrange’s interpolation formula
