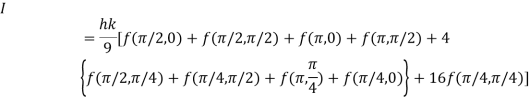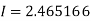Unit - 4
Numerical differentiation and integration
Q1) Given that
X | 1.0 | 1.1 | 1.2 | 1.3 |
Y | 0.841 | 0.891 | 0.932 | 0.963 |
Find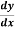 
at 
.
A1)
Here the first derivative is to be calculated at the beginning of the table, therefore forward difference formula will be used
Forward difference table is given below:
X | Y |  |  |  |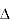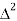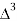
1.0
1.1
1.2
1.3 | 0.841
0.891
0.932
0.962 |
0.050
0.041
0.031 |
-0.009
-0.010 |
-0.001 |
By Newton’s forward differentiation formula for differentiation
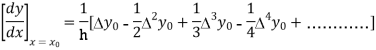
Here 
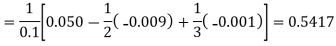
Q2) Find the first and second derivatives of the function given below at the point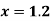 
:
X | 1 | 2 | 3 | 4 | 5 |
Y | 0 | 1 | 5 | 6 | 8 |
A2)
Here the point of the calculation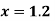 
is at the beginning of the table,
Forward difference table is given by:
X | Y |  |  |  |  |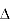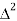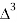
1
2
3
4
5 | 0
1
5
6
8 |
1
4
1
2 |
3
-3
1 |
-6
4
|
-10
|
By Newton’s forward differentiation formula for differentiation
Here 
, 
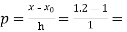0.
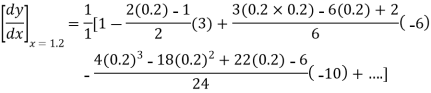
Again
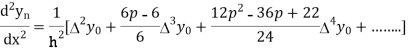
At 
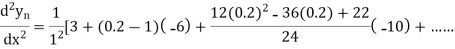
Q3) Given that
X | 0.1 | 0.2 | 0.3 | 0..4 |
Y | 1.10517 | 1.22140 | 1.34986 | 1.49182 |
Find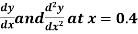 
?
A3)
Backward difference table:
X | Y |  |  |  |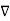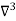
0.1
0.2
0.3
0.4 | 1.10517
1.22140
1.34986
1.49182 |
0.11623
0.12846
0.14196 |
0.01223
0.01350 |
0.00127 |
Newton’s Backward formula for differentiation
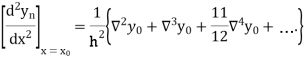
Here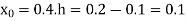 
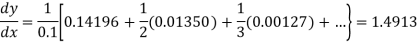
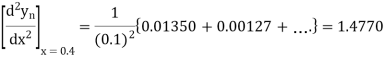
Q4) State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:
(0, 23), (0.5, 19), (1.0, 14), (1.5, 11), (2.0, 12.5), (2.5, 16), (3.0, 19), (3.5, 20), (4.0, 20).
Estimate the area bounded by the curve, the x axis and the extreme ordinates.
A4)
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =
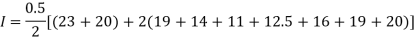
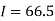
Q5) Evaluate using trapezoidal rule with five ordinates
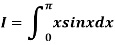
Here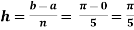 
A5)
We construct the data table:
X | 0 |  |  |  |  |  |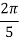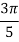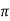
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
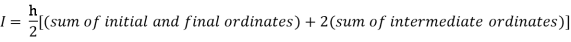
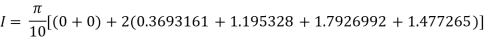
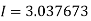
Q6) Evaluate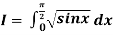 
Using Simpson’s 1/3 rule with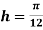 
.
A6)
For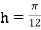 
, we construct the data table:
X | 0 |  |  |  |  |  |  |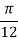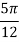
 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule
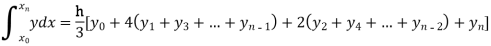
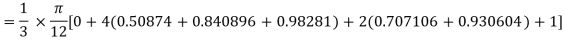
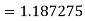
Q7) Evaluate 
A7)
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4. 4 | 4.6 | 4.8 | 5.0 | 5.2 |
Y=logx | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
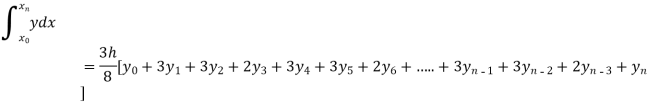
= 1.8278475
Q8) Evaluate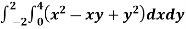 
A8)
Let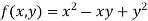 
Here the interval of x and y are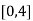 
and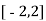 
.
Let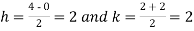 
Consider the following table:
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
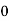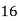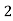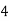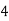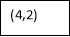
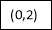
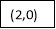
Or
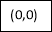
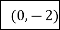
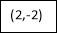
By Trapezoidal Rule
.
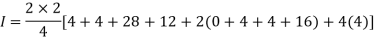
Q9) Evaluate 
A9)
Let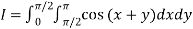 
And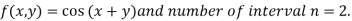 
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
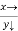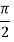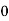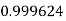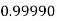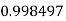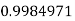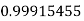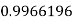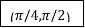
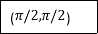
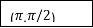Or
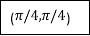
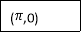
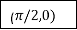
By Trapezoidal Rule
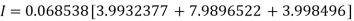
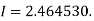
Q10) Evaluate 
A10)
Let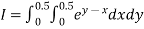 
Here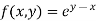 
Let the number of intervals be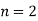 
.
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
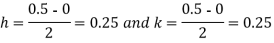
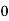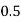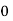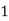
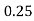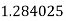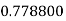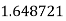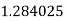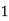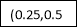
Or
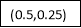
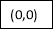
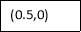
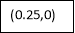
By Simpson’s 1/3 Rule
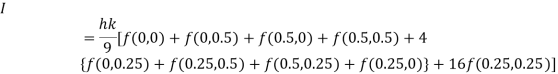
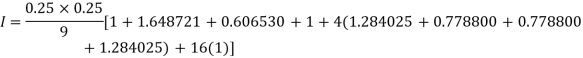
Q11) Evaluate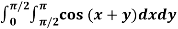 
A11)
Let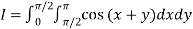 
And 
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
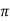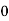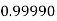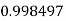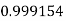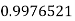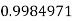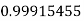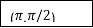Or
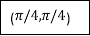
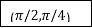
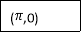
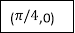
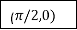
By Simpson’s 1/3 Rule
