Unit - 6
Solution of Ordinary Differential Equation (ODE)
Q1) Solve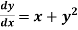 ,
, 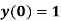 using Taylor’s series method and compute
using Taylor’s series method and compute 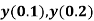 .
.
A1)
Here  This implies that
This implies that  .
.
Differentiating, we get
 .
.
 .
.
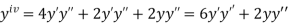
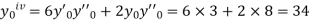 .
.
The Taylor’s series at 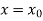 ,
,
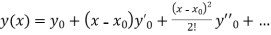
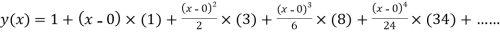
 (1)
(1)
At 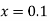 in equation (1) we get
in equation (1) we get

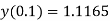
At 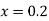 in equation (1) we get
in equation (1) we get
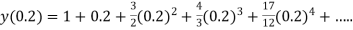
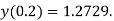
Q2) Using Taylor’s series method, find the solution of
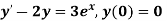
At 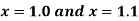 ?
?
A2)
Here 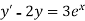
At 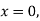 implies that
implies that 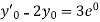 or
or  or
or 
Differentiating, we get
 implies that
implies that 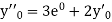 or
or  .
.
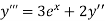 implies that
implies that 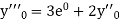 or
or 
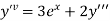 implies that
implies that 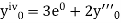 or
or 
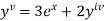 implies that
implies that 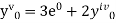 or
or 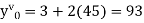
The Taylor’s series at 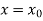 ,
,
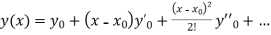
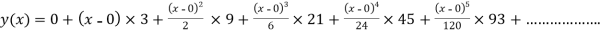
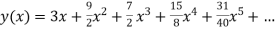 (1)
(1)
At 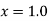 in equation (1) we get
in equation (1) we get
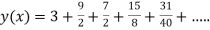
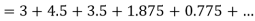
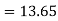
At 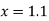 in equation (1) we get
in equation (1) we get
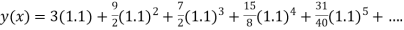
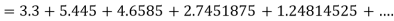
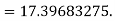
Q3) Use Euler’s method to find y(0.4) from the differential equation
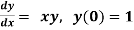 with h=0.1
with h=0.1
A3)
Given equation 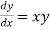
Here 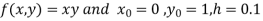
We break the interval in four steps.
So that 
By Euler’s formula
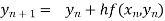 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
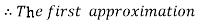
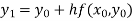
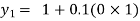

For n=1 in equation (i) we get



 .01
.01
For n=2 in equation (i) we get

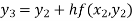

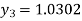
For n=3 in equation (i) we get

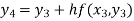
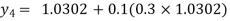
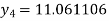
Hence y(0.4) =1.061106.
Q4) Given 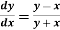 with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method (five steps).
with the initial condition y=1 at x=0. Find y for x=0.1 by Euler’s method (five steps).
A4)
Given equation is 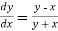
Here 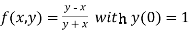
No. Of steps n=5 and so that 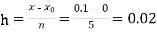
So that 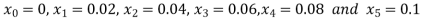
Also 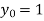
By Euler’s formula
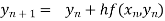 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
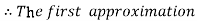

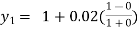
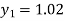
For n=1 in equation (i) we get
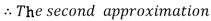
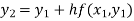
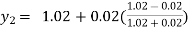

For n=2 in equation (i) we get
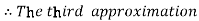
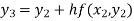

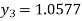
For n=3 in equation (i) we get
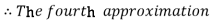
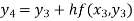
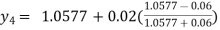
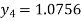
For n=4 in equation (i) we get
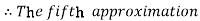
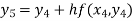

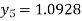
Hence 
Q5) Use modified Euler’s method to compute y for x=0.05. Given that
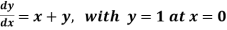
A5)
Result correct to three decimal places.
Given equation 
Here 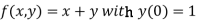
Take h = 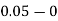 = 0.05
= 0.05
By modified Euler’s formula the initial iteration is

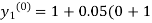 )
)
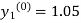
The iteration formula by modified Euler’s method is
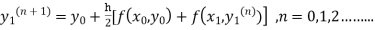 -----(i)
-----(i)
For n=0 in equation (i) we get
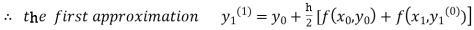
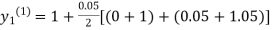
Where 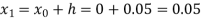 and
and 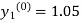 as above
as above
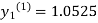
For n=1 in equation (i) we get
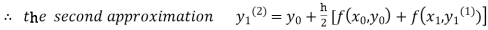
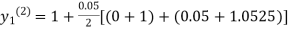
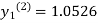
For n=3 in equation (i) we get
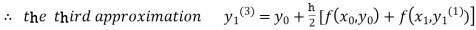


Since third and fourth approximation are equal.
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Q6) Using modified Euler’s method, obtain a solution of the equation
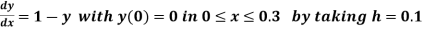
A6)
Given equation 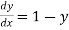
Here 
By modified Euler’s formula the initial iteration is
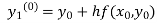
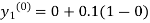

The iteration formula by modified Euler’s method is
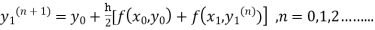 -----(i)
-----(i)
For n=0 in equation (i) we get
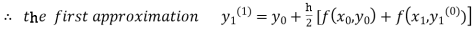
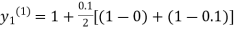
Where 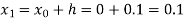 and
and 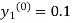 as above
as above

For n=1 in equation (i) we get

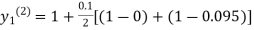

For n=2 in equation (i) we get
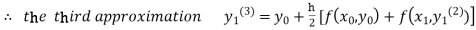
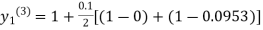
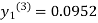
For n=3 in equation (i) we get

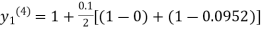

Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of  at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is

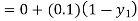
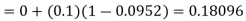
The iteration formula by modified Euler’s method is
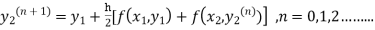 -----(ii)
-----(ii)
For n=0 in equation (ii) we get


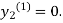 1814
1814
For n=1 in equation (ii) we get
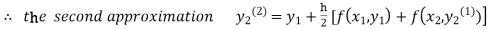

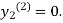 1814
1814
Since first and second approximation are equal.
Hence y = 0.1814 at x=0.2
To calculate the value of 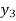 at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is
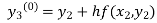
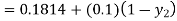
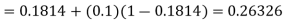
The iteration formula by modified Euler’s method is
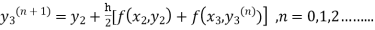 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
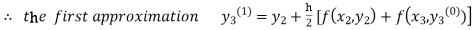
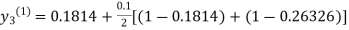

For n=1 in equation (iii) we get
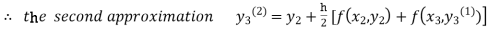
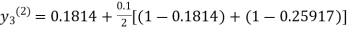
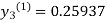
For n=2 in equation (iii) we get
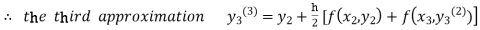


For n=3 in equation (iii) we get
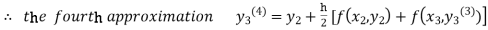
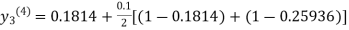
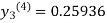
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
Q7) Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that
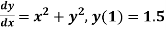
A7)
Given equation 
Here 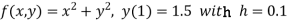
Also 
By Runge Kutta formula for first interval
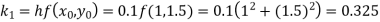
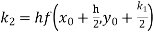
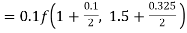
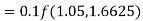

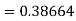
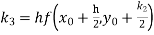

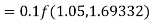


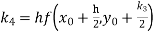
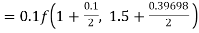
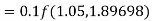

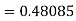
Again 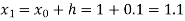
A fourth order Runge Kutta formula:
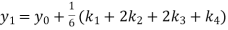
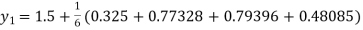
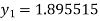
To find y at 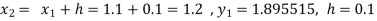
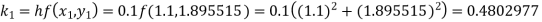
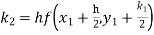

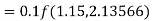

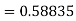
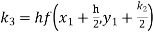
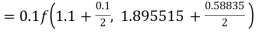
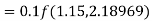

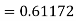
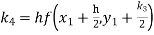
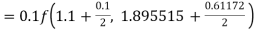

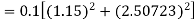

A fourth order Runge Kutta formula:
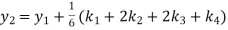
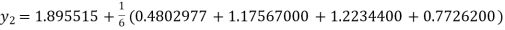
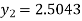
Q8) Using Runge Kutta method of order four, solve  to find
to find 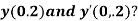
A8)
Given second order differential equation is
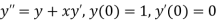
Let 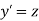 then above equation reduces to
then above equation reduces to
Or 
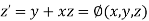 (say)
(say)
Or 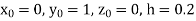 .
.
By Runge Kutta Method we have
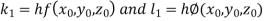
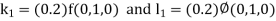


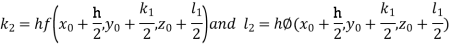
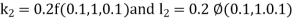
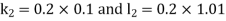
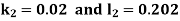
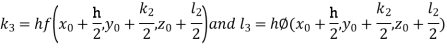

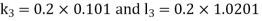
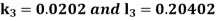
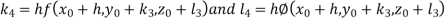
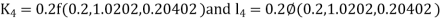
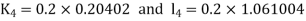

A fourth order Runge Kutta formula:
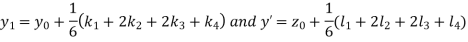
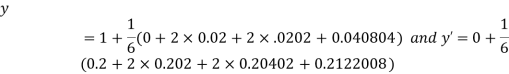
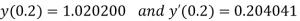
Q9) Use Jacobi’s method to solve the system of equations:

A9)
Since 
So, we express the unknown with large coefficient in terms of other coefficients.

 (1)
(1)
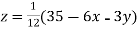
Let the initial approximation be 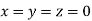
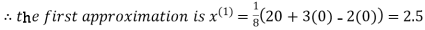

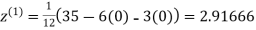
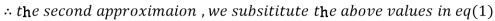

 2.35606
2.35606
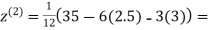 0.91666
0.91666
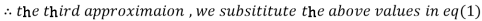
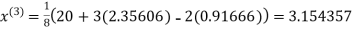
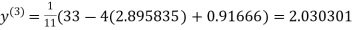

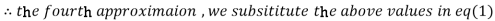
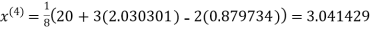
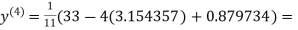 1.932936
1.932936
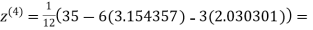 0.831912
0.831912
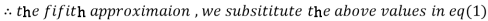
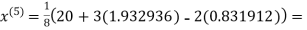 3.016873
3.016873
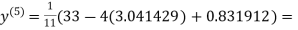 1.969654
1.969654


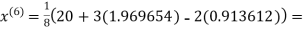 3.010217
3.010217
 1.986010
1.986010
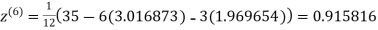
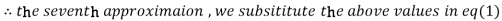

 1.988631
1.988631
 0.915055
0.915055
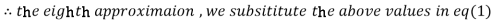

 1.986532
1.986532
 0.911609
0.911609
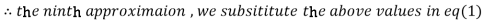

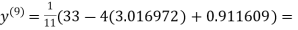 1.985792
1.985792
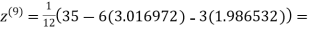 0.911547
0.911547
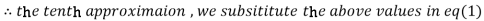
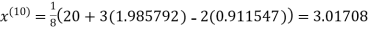
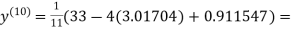 1.98576
1.98576
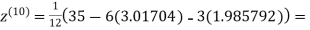 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 
Q10) Use Jacobi’s method to solve the system of the equations

A10)
Rewrite the given equations
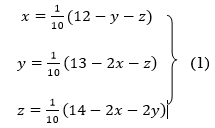
Let the initial approximation be 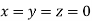

 1.2
1.2
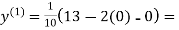 1.3
1.3
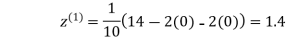
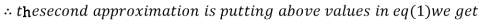
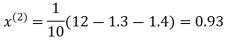
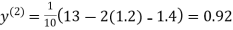
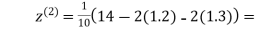 0.9
0.9



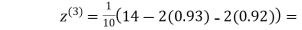 1.03
1.03
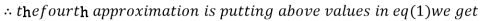
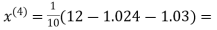 0.9946
0.9946
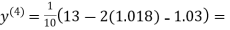 0.9934
0.9934
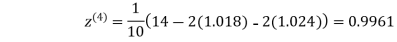

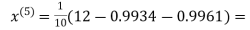 1.0015
1.0015
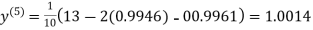
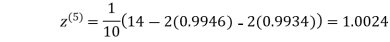
Hence the solution of the above equation correct to two decimal places is
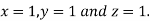
Q11) Solve the following system of equations
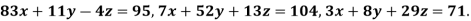 By Gauss-Seidel method.
By Gauss-Seidel method.
A11)
Rewrite the given system of equations as
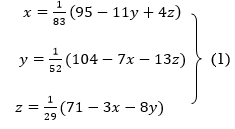
Let the initial approximation be 
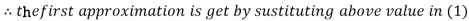


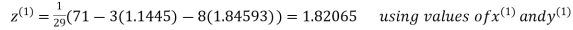
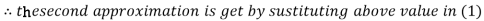

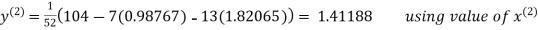
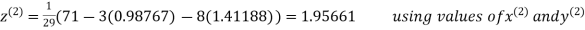
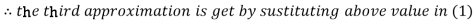
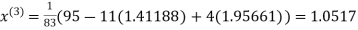
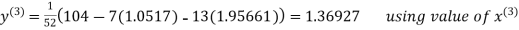
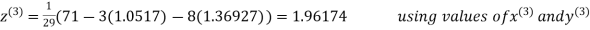
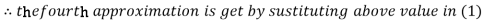
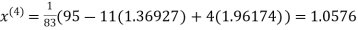
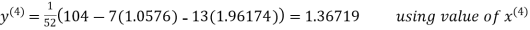
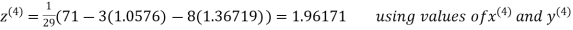
Thus the required solution is 