Unit II
Searching and Sorting Algorithms
Big-oh notations can be express by using ‘o’ symbol. This notation indicates the maximum number of steps required to solve the problem. This notation expresses the worst case growth of an algorithm. Consider the following diagram in which there are two functions f(x) and g(x). f(x) is more complex than the function g(x).
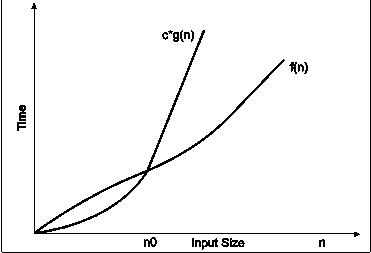
Fig.
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c(n) which bound function f(n) at some point n0. Beyond the point ‘n0’ function c*g(n) is always greater than f(n).
Now f(n)=Og(n)if there is some constant ‘c’ and some initial value ‘n0’. such that f(n)<=c*g(n) for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
Consider the following example
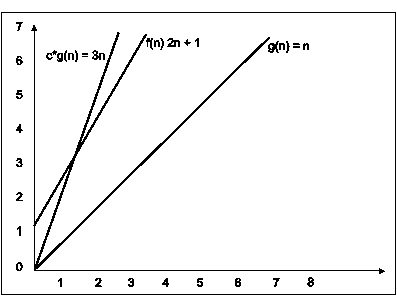
Fig.
In the above example g(n) is ‘’n’ and f(n) is ‘2n+1’ and value of constant is 3. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c*g(n) is always greater than f(n) for constant ‘3’. We can write the conclusion as follows
f(n)=O g(n) for constant ‘c’ =3 and ‘n0’=1
such that f(n)<=c*g(n) for all n>n0
2. Big-omega notation of Asymptotic Notations
Big-omega notations can be express by using ‘Ω’ symbol. This notation indicates the minimum number of steps required to solve the problem. This notation expresses the best case growth of an algorithm. Consider the following diagram in which there are two functions f(n) and g(n). f(n) is more complex than the function g(n).
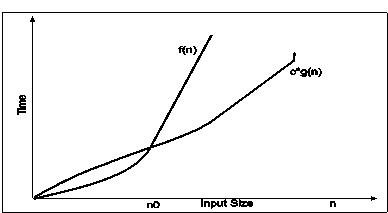
Fig.
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c(n) which bound function f(n) at some point n0. Beyond the point ‘n0’ function c*g(n) is always smaller than f(n).
Now f(n)=Ωg(n)if there is some constant ‘c’ and some initial value ‘n0’. such that c*g(n) <= f(n)for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
Consider the following example
In the above example g(n) is ‘2n’ and f(n) is ‘2n-2’ and value of constant is 0.5. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c*g(n) is always smaller than f(n) for constant ‘0.5’. We can write the conclusion as follows
f(n) = Ω g(n) for constant ‘c’ =0.5 and ‘n0’=2
such that c*g(n)<= f(n) for all n>n0
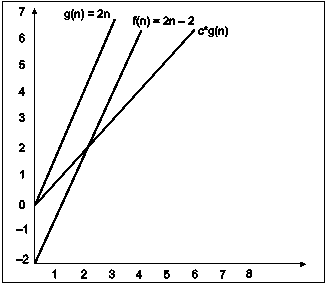
Fig.
3. Explain Big-theta notation
Big-theta notations can be express by using ‘Ɵ’ symbol. This notation indicates the exact number of steps required to solve the problem. This notation expresses the average case growth of an algorithm. Consider the following diagram in which there are two functions f(n) and g(n). f(n) is more complex than the function g(n).
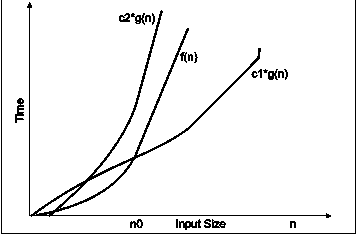
Fig.
In the above diagram out of two function f(n) and g(n), more complex function is f(n), so need to relate its growth as compare to simple function g(n). More specifically we need one constant function c1 and c2 which bound function f(n) at some point n0. Beyond the point ‘n0’ function c1*g(n) is always smaller than f(n) and c2*g(n) is always greater than f(n).
Now f(n) = g(n) if there is some constant ‘c1 and c2’ and some initial value ‘n0’. such that c1*g(n) <= f(n)<=c2*g(n)for all n>n0
In the above expression ‘n’ represents the input size
f(n) represents the time that algorithm will take
f(n) and g(n) are non-negative functions.
f(n) = g(n) if and only if f(n)=O g(n) and f(n)=Ω g(n)
Consider the following example
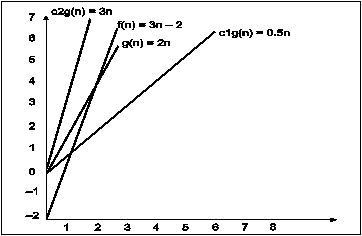
Fig.
In the above example g(n) is ‘2n’ and f(n) is ‘3n-2’ and value of constant c1 is 0.5 and c2 is 2. The point where c*g(n) and f(n) intersect is ‘’n0’. Beyond ‘n0’ c1*g(n) is always smaller than f(n) for constant ‘0.5’ and c2*g(n) is always greater than f(n) for constant ‘2’. We can write the conclusion as follows
f(n)=Ω g(n) for constant ‘c1’ =0.5 , ‘c2’ = 2 and ‘n0’=2
such that c1*g(n)<= f(n)<=c2*g(n) for all n>n0
4. Write a program for linear search
#include<stdio.h>
#include<conio.h>
int search(int [],int, int);
void main()
{
int a[20],k,i,n,m;
clrscr();
printf(“\n\n ENTER THE SIZE OF ARRAY”);
scanf(“%d”,&n);
printf(“\n\nENTER THE ARRAY ELEMENTS\n\n”);
for(i=0;i<n;i++)
{
scanf(“%d”,&a[i]);
}
printf(“\n\nENTER THE ELEMENT FOR SEARCH\n”);
scanf(“%d”,&k);
m=search(a,n,k);
if(m==–1)
{
printf(“\n\nELEMENT IS NOT FOUND IN LIST”);
}
else
{
printf(“\n\nELEMENT IS FOUND AT LOCATION %d”,m);
}
}
getch();
}
int search(int a[],int n,int k)
{
int i;
for(i=0;i<n;i++)
{
if(a[i]==k)
{
return i;
}
}
if(i==n)
{
return –1;
}
}
5. Give an Example of binary search.
Let array A= {–1, 5, 6, 18, 19, 25, 46, 78, 102, 114}. We want to find element ‘6’ using binary search.
–1 | 5 | 6 | 18 | 19 | 25 | 46 | 78 | 102 | 114 |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Solution:
Step 1 : Low=0, High= 9
Step 2 : Mid=(Low + High)/2
Mid = (0+9)/2 =4.5 i.e 4. It means middle element is located at position 4. So A[Mid] is 19.Thus
Low=0
Mid=4
High=9
Low |
|
|
| Mid |
|
|
|
| High |
–1 | 5 | 6 | 18 | 19 | 25 | 46 | 78 | 102 | 114 |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Step 3 : Compare 6 with 19. It satisfies case 2 of step 3. so High= 4–1=3 and element is present in left half of array. We can ignore right half of array.
Repeat step 2. So mid= (0+3)/2 = 1.5 i.e 1. mid is at position 1. Element 5 is present at position 1.
Low = 0
Mid = 1
High = 3
Low | Mid |
| High |
|
–1 | 5 | 6 | 18 | 19 |
0 | 1 | 2 | 3 | 4 |
Again compare 5 with 6. It satisfies case 3 of step 3. so
Low = 1+1=2.
Repeat step 2. Mid= (2+ 3)/2= 2.5 i.e 2 .Mid is at position 2. Element 6 is at position 2.
Low=2
Mid=2
High=3
|
| Low, Mid | High |
|
|
|
|
|
|
–1 | 5 | 6 | 18 | 19 |
0 | 1 | 2 | 3 | 4 |
Compare 6 with 6.
Match is found. Return the position and print element found.
6. Write a program for binary search.
#include<stdio.h>
#include<conio.h>
void main()
{
int n,i,search,f=0,low,high,mid,a[20];
clrscr();
printf("Enter the number of elements:");
scanf("%d",&n);
for(i=1;i<=n;i++)
{
printf("Enter the number in ascending order a[%d]=",i);
scanf("%d",&a[i]);
}
printf("Enter the element to be searched:");
scanf("%d",&search);
low=0;
high=n–1;
while(low<=high)
{
mid=(low+high)/2;
if(search<a[mid])
{
high=mid–1;
}
else if(search>a[mid])
{
low=mid+1;
}
else
{
f=1;
printf("Element is found at the position %d:",mid);
exit();
}
}
if(f==0)
{
printf("Element not found");
}
getch();
}
7. Write the Complexity Analysis of Binary Search
Assume our array size is 16.
When n= 16 BinarySearch is called to reduce size to n=8.
When n= 8 BinarySearch is called to reduce size to n=4.
When n= 4 BinarySearch is called to reduce size to n=2.
When n= 2 BinarySearch is called to reduce size to n=1 .
Thus we see that BinarySearch function is called 4 times
i.e. 4 elements of the array were examined for n =16.
Note that 16 = 24
Let us consider a more general case where
n is still a power of 2. Let us say n =2k
After k searches, the while loop is executed k times and n reduces to size 1. Let us assume that each run of the while loop involves at most 4 operations.
Thus total number of operations: 4k.
The value of k can be determined from the expression
2k = n
Taking log of both sides
k = log n
Thus total number of operations = 4 log n.
We conclude that the time complexity of the Binary search method is O(log n), which is much more efficient than the Linear Search method.
8. Explain Fibonacci Search
Fibonacci series generates the subsequent number by adding two previous numbers. Fibonacci series starts from two numbers − F0 & F1. The initial values of F0 & F1 can be taken 0, 1 or 1, 1 respectively.
Fibonacci series satisfies the following conditions −
Fn = Fn-1 + Fn-2
Hence, a Fibonacci series can look like this −
F8 = 0 1 1 2 3 5 8 13
or, this −
F8 = 1 1 2 3 5 8 13 21
Fibonacci Iterative Algorithm
First we try to draft the iterative algorithm for Fibonacci series.
Procedure Fibonacci(n)
declare f0, f1, fib, loop
set f0 to 0
set f1 to 1
display f0, f1
for loop ← 1 to n
fib ← f0 + f1
f0 ← f1
f1 ← fib
display fib
end for
end procedure
Fibonacci Recursive Algorithm
Let us learn how to create a recursive algorithm Fibonacci series. The base criteria of recursion.
START
Procedure Fibonacci(n)
declare f0, f1, fib, loop
set f0 to 0
set f1 to 1
display f0, f1
for loop ← 1 to n
fib ← f0 + f1
f0 ← f1
f1 ← fib
display fib
end for
END
9. Give an example of bubble sort
Suppose the following numbers are stored in an array A:
32 | 51 | 27 | 85 | 66 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
We apply bubble sort to array A. We discuss each pass separately.
Pass 1
1. Compare j[0] and j[1]. Since 32 < 51, the list is not altered.
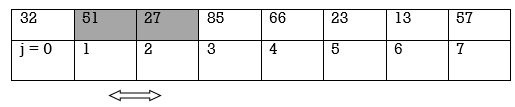
2. Compare j[1] and j[2] Since 51 > 27, interchange 51 and 27 as follows:
Array A becomes
32 | 27 | 51 | 85 | 66 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
3. Compare j[2] and j[3]. Since 51 < 85, array is not altered.
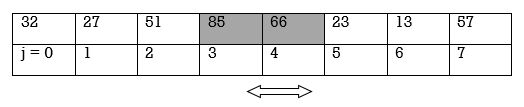
4. Compare j[3] and j[4]. Since 85 > 66, interchange 85 and 66 as follows:
Array A becomes
32 | 27 | 51 | 66 | 85 | 23 | 13 | 57 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
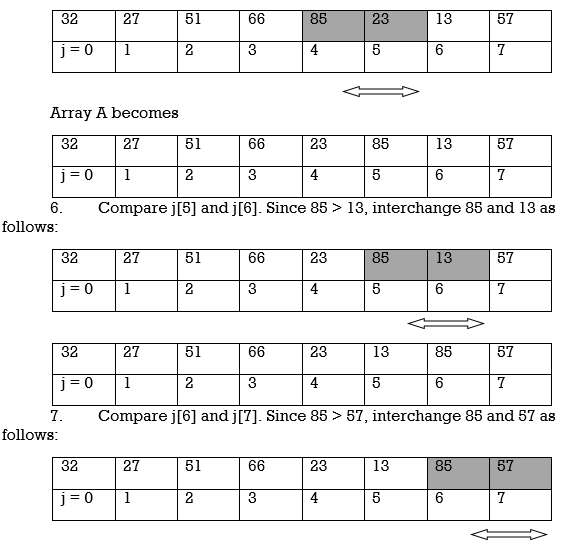
5. Compare j[4] and j[5]. Since 85 > 23, interchange 85 and 23 as follows:
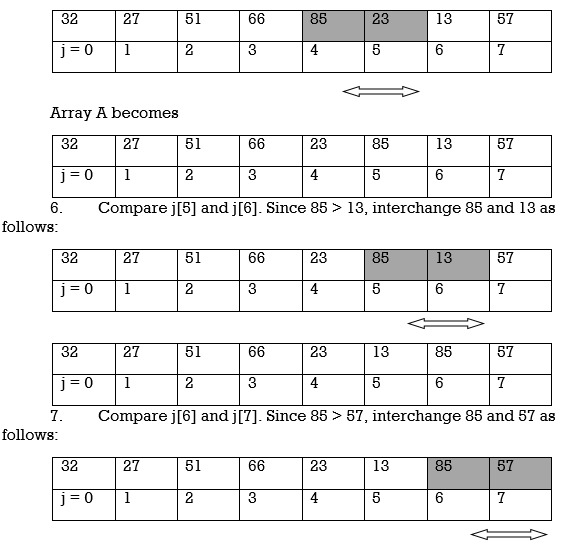
Array A becomes
32 | 27 | 51 | 66 | 23 | 13 | 57 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
At the end of this first pass, the largest number, 85, has moved to the last position. However, the rest of the numbers are not sorted, even though some of them have changed their positions.
Pass 2 will move second last number at second last position, Pass 3 will move third last number at third last position and so on. Here we show array after every pass.
Pass 2 :
27 | 33 | 51 | 23 | 13 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 3 :
27 | 33 | 23 | 13 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 4:
27 | 23 | 13 | 33 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 5 :
23 | 13 | 27 | 33 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pass 6 :
13 | 23 | 27 | 33 | 51 | 57 | 66 | 85 |
j = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Hence the array is sorted in 6 passes.
10. Explain Insertion sort with example.
Insertion Sort reads all elements from 1 to n and inserts each element at its proper position. This sorting method works well on small list of elements.
Procedure for each pass is as follows.
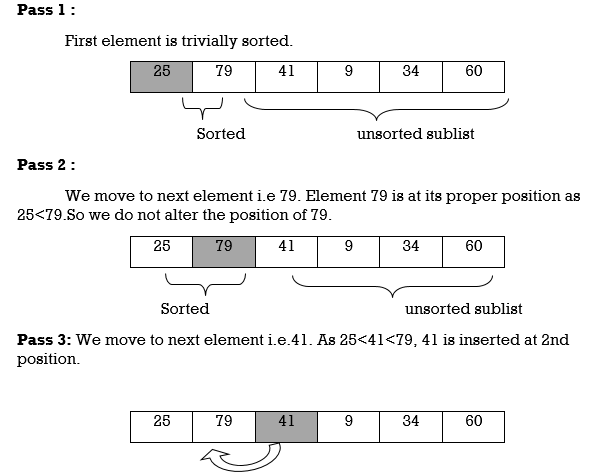
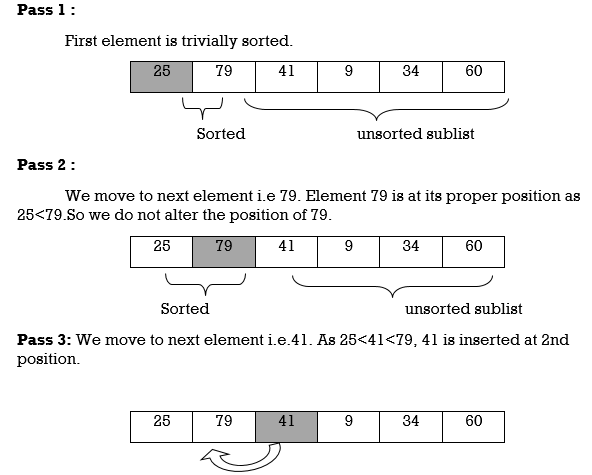
Pass 1 :
A[l] by itself is trivially sorted.
Pass 2 :
A[2] is inserted either before or after A[l] so that: A[l], A[2] is sorted.
Pass 3 :
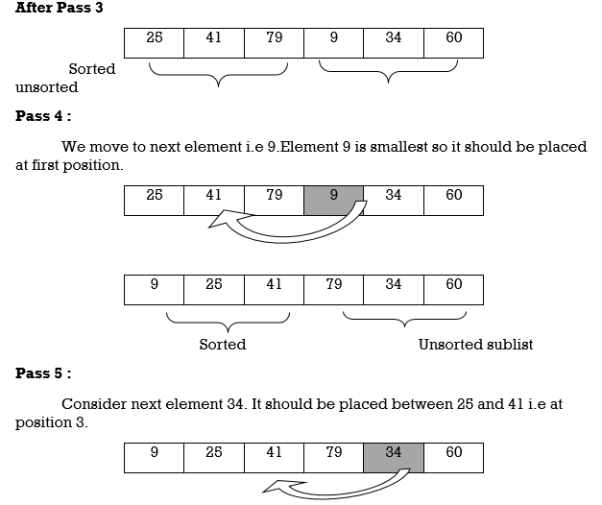
A[3] is inserted into its proper place so that: A[l], A[2], A[3] is sorted.
Pass 4 :
A[4] is inserted into its proper place A[l], A[2], A[3], A[4] is sorted.
Pass N :
A[N] is inserted into its proper place in so that:
A[l], A[ 2 ] , . . . , A[ N ] is sorted
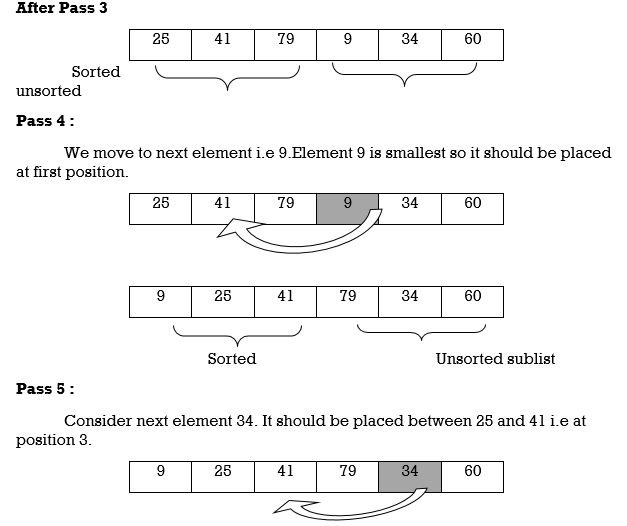
Example: We will apply insertion sort on original list of Fig.3.Assume we are arranging elements in ascending order.
25 | 79 | 41 | 9 | 34 | 60 |
Fig. 4.3 : Original List
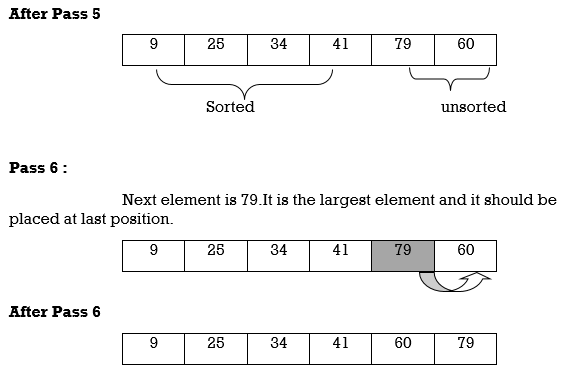
Hence the list is sorted using insertion sort.
We will see one more example.
Apply Insertion sort on array A= {77,30,40,10,88,20,65,56}
Hence the list is sorted using Insertion sort.