undefined | unit 5 trees

Unit V

Trees

What are the Basic Tree Concepts?

A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.

Definition of TREE:

A tree is defined as a set of one or more nodes T such that:

There is a specially designed node called root node

The remaining nodes are partitioned into N disjoint set of nodes T1, T2,…..Tn, each of which is a tree.

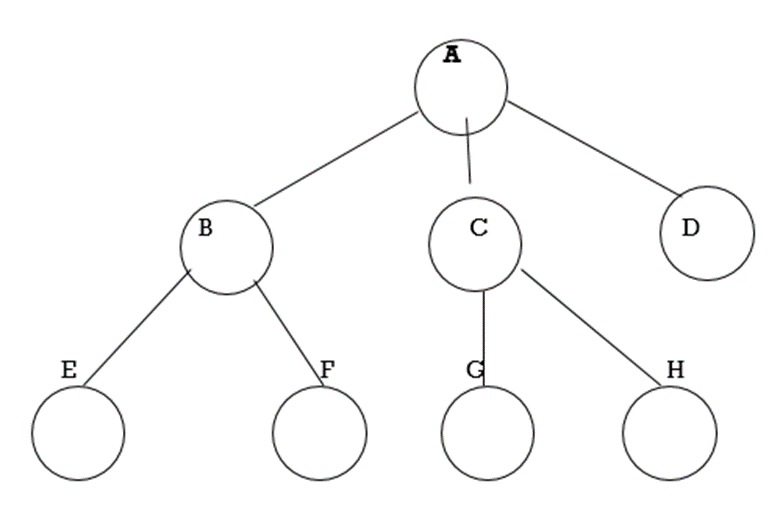
Fig. Example of tree

In above tree A is Root.

Remaining nodes are partitioned into three disjoint sets:

{B, E, F}, {C, G, H}, {D}.

All these sets satisfies the properties of tree.

Some examples of TREE and NOT TREE

Each linear list is trivially a tree

Not a tree: cycle A→A

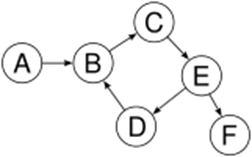
Not a tree: cycle B→C→E→D→B

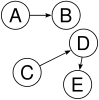
Not a tree: two non-(connected parts, A→B and C→D→E

Not a tree: undirected cycle 1-2-4-3

Fig. Examples of tree and no tree

2. Define binary tree and what are the tree terminologies?

A binary tree is made of nodes, where each node contains a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller "subtrees" on either side. A null pointer represents a binary tree with no elements -- the empty tree.

The formal recursive definition is A binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.

Example of Binary Tree:

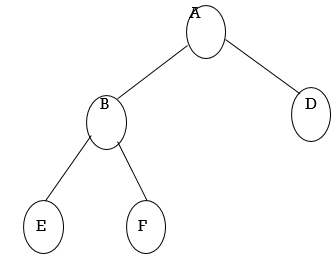
Fig. Example of Binary Tree

Tree Terminologies

Root – The top node in a tree.

Parent – The converse notion of child.

Siblings – Nodes with the same parent.

Descendant – a node reachable by repeated proceeding from parent to child.

Ancestor – a node reachable by repeated proceeding from child to parent.

Leaf – a node with no children.

Internal node – a node with at least one child.

External node – a node with no children.

Degree – number of sub trees of a node.

Edge – connection between one node to another.

Path – a sequence of nodes and edges connecting a node with a descendant.

Level – The level of a node is defined by 1 + the number of connections between the node and the root.

Height of tree –The height of a tree is the number of edges on the longest downward path between the root and a leaf.

Height of node –The height of a node is the number of edges on the longest downward path between that node and a leaf.

Depth –The depth of a node is the number of edges from the node to the tree's root node.

Forest – A forest is a set of n ≥ 0 disjoint trees.

3. What are different types of tree?

The tree data structure can be classified into six different categories.

Tree

General Tree

General Tree stores the elements in a hierarchical order in which the top level element is always present at level 0 as the root element. All the nodes except the root node are present at number of levels. The nodes which are present on the same level are called siblings while the nodes which are present on the different levels exhibit the parent-child relationship among them. A node may contain any number of sub-trees. The tree in which each node contain 3 sub-tree, is called ternary tree.

Forests

Forest can be defined as the set of disjoint trees which can be obtained by deleting the root node and the edges which connects root node to the first level node.

Tree

Binary Tree

Binary tree is a data structure in which each node can have at most 2 children. The node present at the top most level is called the root node. A node with the 0 children is called leaf node. Binary Trees are used in the applications like expression evaluation and many more. We will discuss binary tree in detail, later in this tutorial.

Binary Search Tree

Binary search tree is an ordered binary tree. All the elements in the left sub-tree are less than the root while elements present in the right sub-tree are greater than or equal to the root node element. Binary search trees are used in most of the applications of computer science domain like searching, sorting, etc.

Expression Tree

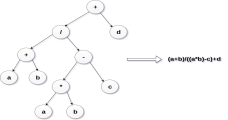
Expression trees are used to evaluate the simple arithmetic expressions. Expression tree is basically a binary tree where internal nodes are represented by operators while the leaf nodes are represented by operands. Expression trees are widely used to solve algebraic expressions like (a+b)*(a-b). Consider the following example.

Q. Construct an expression tree by using the following algebraic expression.

(a + b) / (a*b - c) + d

Tree

Tournament Tree

Tournament tree are used to record the winner of the match in each round being played between two players. Tournament tree can also be called as selection tree or winner tree. External nodes represent the players among which a match is being played while the internal nodes represent the winner of the match played. At the top most level, the winner of the tournament is present as the root node of the tree.

For example, tree .of a chess tournament being played among 4 players is shown as follows. However, the winner in the left sub-tree will play against the winner of right sub-tree.

Tree

4. Explain Binary Tree representation

There are two types of representation of a binary tree:

1. Linked Representation

In this representation, the binary tree is stored in the memory, in the form of a linked list where the number of nodes are stored at non-contiguous memory locations and linked together by inheriting parent child relationship like a tree. every node contains three parts : pointer to the left node, data element and pointer to the right node. Each binary tree has a root pointer which points to the root node of the binary tree. In an empty binary tree, the root pointer will point to null.

Consider the binary tree given in the figure below.

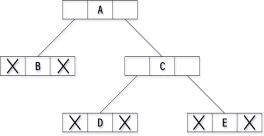
Binary Tree

In the above figure, a tree is seen as the collection of nodes where each node contains three parts : left pointer, data element and right pointer. Left pointer stores the address of the left child while the right pointer stores the address of the right child. The leaf node contains null in its left and right pointers.

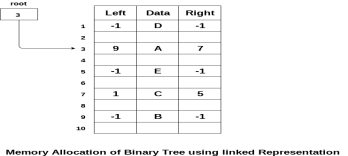
The following image shows about how the memory will be allocated for the binary tree by using linked representation. There is a special pointer maintained in the memory which points to the root node of the tree. Every node in the tree contains the address of its left and right child. Leaf node contains null in its left and right pointers.

Binary Tree

2. Sequential Representation

This is the simplest memory allocation technique to store the tree elements but it is an inefficient technique since it requires a lot of space to store the tree elements. A binary tree is shown in the following figure along with its memory allocation.

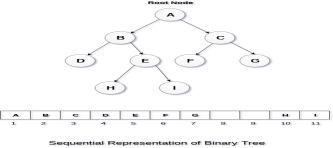
Binary Tree

In this representation, an array is used to store the tree elements. Size of the array will be equal to the number of nodes present in the tree. The root node of the tree will be present at the 1st index of the array. If a node is stored at ith index then its left and right children will be stored at 2i and 2i+1 location. If the 1st index of the array i.e. tree[1] is 0, it means that the tree is empty.

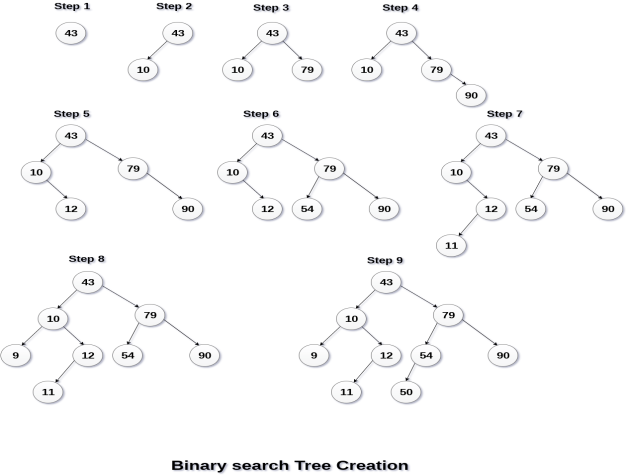
5. Create the binary search tree using the following data elements.

43, 10, 79, 90, 12, 54, 11, 9, 50

Insert 43 into the tree as the root of the tree.

Read the next element, if it is lesser than the root node element, insert it as the root of the left sub-tree.

Otherwise, insert it as the root of the right of the right sub-tree.

The process of creating BST by using the given elements, is shown in the image below.

Binary Search Tree

6. Write a Program to implement BST operations

#include <iostream>

#include <stdlib.h>

using namespace std;

struct Node {

int data;

Node *left;

Node *right;

};

Node* create(int item)

{

Node* node = new Node;

node->data = item;

node->left = node->right = NULL;

return node;

}

void inorder(Node *root)

{

if (root == NULL)

return;

inorder(root->left);

cout<< root->data << " ";

inorder(root->right);

}

Node* findMinimum(Node* cur)

{

while(cur->left != NULL) {

cur = cur->left;

}

return cur;

}

Node* insertion(Node* root, int item)

{

if (root == NULL)

return create(item);

if (item < root->data)

root->left = insertion(root->left, item);

else

root->right = insertion(root->right, item);

return root;

}

void search(Node* &cur, int item, Node* &parent)

{

while (cur != NULL && cur->data != item)

{

parent = cur;

if (item < cur->data)

cur = cur->left;

else

cur = cur->right;

}

void deletion(Node*& root, int item)

{

Node* parent = NULL;

Node* cur = root;

search(cur, item, parent);

if (cur == NULL)

return;

if (cur->left == NULL && cur->right == NULL)

{

if (cur != root)

{

if (parent->left == cur)

parent->left = NULL;

else

parent->right = NULL;

}

else

root = NULL;

free(cur);

}

else if (cur->left && cur->right)

{

Node* succ = findMinimum(cur- >right);

int val = succ->data;

deletion(root, succ->data);

cur->data = val;

}

else

{

Node* child = (cur->left)? Cur- >left: cur->right;

if (cur != root)

{

if (cur == parent->left)

parent->left = child;

else

parent->right = child;

}

else

root = child;

free(cur);

}

int main()

{

Node* root = NULL;

int keys[8];

for(int i=0;i<8;i++)

{

cout << "Enter value to be inserted";

cin>>keys[i];

root = insertion(root, keys[i]);

}

inorder(root);

cout<<"\n";

deletion(root, 10);

inorder(root);

return 0;

}

Output:

Enter value to be inserted? 10

Enter value to be inserted? 20

Enter value to be inserted? 30

Enter value to be inserted? 40

Enter value to be inserted? 5

Enter value to be inserted? 25

Enter value to be inserted? 15

Enter value to be inserted? 5

5 5 10 15 20 25 30 40

5 5 15 20 25 30 40

7. Explain in detail AVL tree.

AVL Tree is invented by GM Adelson - Velsky and EM Landis in 1962. The tree is named AVL in honour of its inventors.

AVL Tree can be defined as height balanced binary search tree in which each node is associated with a balance factor which is calculated by subtracting the height of its right sub-tree from that of its left sub-tree.

Tree is said to be balanced if balance factor of each node is in between -1 to 1, otherwise, the tree will be unbalanced and need to be balanced.

Balance Factor (k) = height (left(k)) - height (right(k))

If balance factor of any node is 1, it means that the left sub-tree is one level higher than the right sub-tree.

If balance factor of any node is 0, it means that the left sub-tree and right sub-tree contain equal height.

If balance factor of any node is -1, it means that the left sub-tree is one level lower than the right sub-tree.

An AVL tree is given in the following figure. We can see that, balance factor associated with each node is in between -1 and +1. therefore, it is an example of AVL tree.

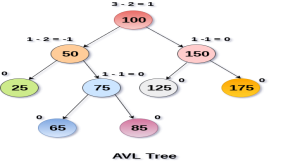
AVL Tree

Complexity

Algorithm	Average case	Worst case
Space	o(n)	o(n)
Search	o(log n)	o(log n)
Insert	o(log n)	o(log n)
Delete	o(log n)	o(log n)

Operations on AVL tree

Due to the fact that, AVL tree is also a binary search tree therefore, all the operations are performed in the same way as they are performed in a binary search tree. Searching and traversing do not lead to the violation in property of AVL tree. However, insertion and deletion are the operations which can violate this property and therefore, they need to be revisited.

SN	Operation	Description
1	Insertion	Insertion in AVL tree is performed in the same way as it is performed in a binary search tree. However, it may lead to violation in the AVL tree property and therefore the tree may need balancing. The tree can be balanced by applying rotations.
2	Deletion	Deletion can also be performed in the same way as it is performed in a binary search tree. Deletion may also disturb the balance of the tree therefore, various types of rotations are used to rebalance the tree.

Why AVL Tree ?

AVL tree controls the height of the binary search tree by not letting it to be skewed. The time taken for all operations in a binary search tree of height h is O(h). However, it can be extended to O(n) if the BST becomes skewed (i.e. worst case). By limiting this height to log n, AVL tree imposes an upper bound on each operation to be O(log n) where n is the number of nodes.

8. What is the different operation of B Tree explain in detail with examples?

Searching :

Searching in B Trees is similar to that in Binary search tree. For example, if we search for an item 49 in the following B Tree. The process will something like following :

Compare item 49 with root node 78. since 49 < 78 hence, move to its left sub-tree.

Since, 40<49<56, traverse right sub-tree of 40.

49>45, move to right. Compare 49.

match found, return.

Searching in a B tree depends upon the height of the tree. The search algorithm takes O(log n) time to search any element in a B tree.

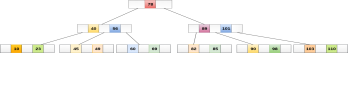
B Tree

Inserting

Insertions are done at the leaf node level. The following algorithm needs to be followed in order to insert an item into B Tree.

Traverse the B Tree in order to find the appropriate leaf node at which the node can be inserted.

If the leaf node contain less than m-1 keys then insert the element in the increasing order.

Else, if the leaf node contains m-1 keys, then follow the following steps.

Insert the new element in the increasing order of elements.
Split the node into the two nodes at the median.
Push the median element upto its parent node.
If the parent node also contain m-1 number of keys, then split it too by following the same steps.

Example:

Insert the node 8 into the B Tree of order 5 shown in the following image.

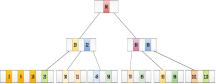
B Tree

8 will be inserted to the right of 5, therefore insert 8.

B Tree

The node, now contain 5 keys which is greater than (5 -1 = 4 ) keys. Therefore split the node from the median i.e. 8 and push it up to its parent node shown as follows.

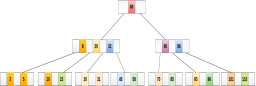
B Tree

Deletion

Deletion is also performed at the leaf nodes. The node which is to be deleted can either be a leaf node or an internal node. Following algorithm needs to be followed in order to delete a node from a B tree.

Locate the leaf node.

If there are more than m/2 keys in the leaf node then delete the desired key from the node.

If the leaf node doesn't contain m/2 keys then complete the keys by taking the element from eight or left sibling.

If the left sibling contains more than m/2 elements then push its largest element up to its parent and move the intervening element down to the node where the key is deleted.
If the right sibling contains more than m/2 elements then push its smallest element up to the parent and move intervening element down to the node where the key is deleted.

If neither of the sibling contain more than m/2 elements then create a new leaf node by joining two leaf nodes and the intervening element of the parent node.

If parent is left with less than m/2 nodes then, apply the above process on the parent too.

If the the node which is to be deleted is an internal node, then replace the node with its in-order successor or predecessor. Since, successor or predecessor will always be on the leaf node hence, the process will be similar as the node is being deleted from the leaf node.

Example 1

Delete the node 53 from the B Tree of order 5 shown in the following figure.

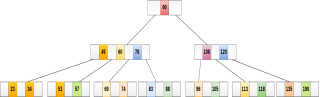
B Tree

53 is present in the right child of element 49. Delete it.

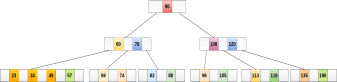
B Tree

Now, 57 is the only element which is left in the node, the minimum number of elements that must be present in a B tree of order 5, is 2. it is less than that, the elements in its left and right sub-tree are also not sufficient therefore, merge it with the left sibling and intervening element of parent i.e. 49.

The final B tree is shown as follows.

B Tree

9. What is the difference between B and B+ tree?

SN	B Tree	B+ Tree
1	Search keys cannot be repeatedly stored.	Redundant search keys can be present.
2	Data can be stored in leaf nodes as well as internal nodes	Data can only be stored on the leaf nodes.
3	Searching for some data is a slower process since data can be found on internal nodes as well as on the leaf nodes.	Searching is comparatively faster as data can only be found on the leaf nodes.
4	Deletions of internal nodes are so complicated and time consuming.	Deletion will never be a complexed process since element will always be deleted from the leaf nodes.
5	Leaf nodes cannot be linked together.	Leaf nodes are linked together to make the search operations more efficient.

10. Give an example of rotation of a tree.

Example: obtain an AVL tree by inserting one integer at a time in following sequence:

150,155,160,115,110,140,120,145,130

SOLUTION:

Step 1: insert 150

150

Balance factor for 150 is: 0 – 0=0

1500

NO ROTATION IS REQUIRED.

Step 2: insert 155

150-1

1550

Balance factor for 150 is: 0 – 1= -1

Both nodes are balanced.

NO ROATION IS REQIURED.

STEP 3: INSERT 160.

150-2

155-1

1600

Balance factor of 150 is -2. So 150 is unbalanced. Some rotation is required to do 150 as balanced node. Start from 150 towards 160.

150-2 R

155-1 R

1600

We get RR direction. So we have to perform RR rotation.

In RR rotation, Count from unbalanced node. First right node becomes the root node. So here first R is 155. So 155 will become the root.

1550

1500 1600

Now all nodes are balanced.

STEP 4: INSERT 115.

1551

1501 1600

1150

All nodes are balanced. NO ROTATION IS REQUIRED.

STEP 5: INSERT 110

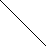1552

1502 1600

1151

1100

155 and 150 are unbalanced. Whenever two/more nodes are unbalanced, we have to consider the lowermost node first. i.e.150. move from 150 towards the node causing unbalancing (110)

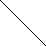
1552

L 1502 1600

L 1151

1100

So we have to perform LL Rotation. In LL rotation, Count from unbalanced node. First Left node becomes the root node. So here first L is 115. So 115 will become the root.

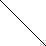
1551

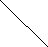1150 1600

1100 1500

Now all nodes are balanced.

STEP 6: INSERT 140 1552

115-1 1600

1100 1501

1400

155 is unbalanced. Count move from 155 towards the node causing unbalancing (140).

1552

115-1 1600

1100 1501

1400

So we have to perform LR Rotation. In LR rotation, Count from unbalanced node(155). Go for left node and then right node (150). 150 will become root node

1500

1150 155-1

1100 1400 1600

Now all nodes are balanced.

STEP 7: INSERT 120

1501

115-1 155-1

1100 1401 1600

1200

Now all nodes are balanced.

STEP 7: INSERT 145

1501

115-1 155-1

1100 1400 1600

1200 1450

Now all nodes are balanced.

STEP 7: INSERT 130

1502

115-2 155-1

1100 1401 1600

120-1 1450

1300

Two nodes 150 and 115 are unbalanced. First consider 115. Count move from 115 towards the node causing unbalancing (130).

1502

115-2 155-1

1100 1401 1600

120-1 1450

1300

So we have to perform RL Rotation. In RL rotation, Count from unbalanced node(115). Go for Right node and then Left node (120). 120 will become root node.

1501

1200 155-1

1150 1400 1600

1100 1300 145

Now all nodes are balanced.

Thus the tree is balanced.

Sign Up