Unit – 2

Combinational Logic Design

The main difference between a half-adder and a full-adder is that the full-adder has three inputs and two outputs. The first two inputs are A and B and the third input is an input carry designated as CIN. When a full adder logic is designed, we will be able to string eight of them together to create a byte-wide adder and cascade the carry bit from one adder to the next.

Design of Half-Adder:

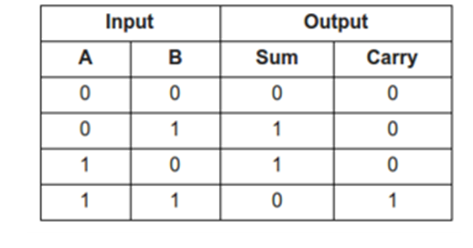
From the truth table, the Boolean expression for SUM and CARRY can be written as:

Sum= A B

Carry= AB

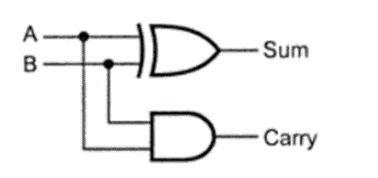
A half-adder can therefore be realized using one XOR Gate and one AND Gate as shown below:

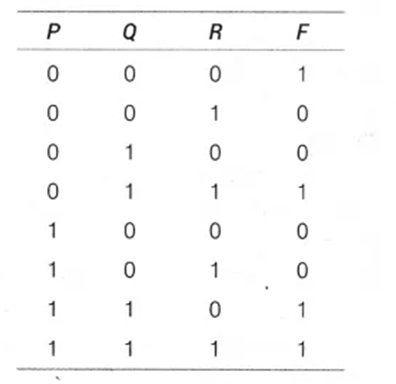
2.     Write the Sum of Product (SOP) form of the function F(P, Q, R) for the following truth table representation of F:

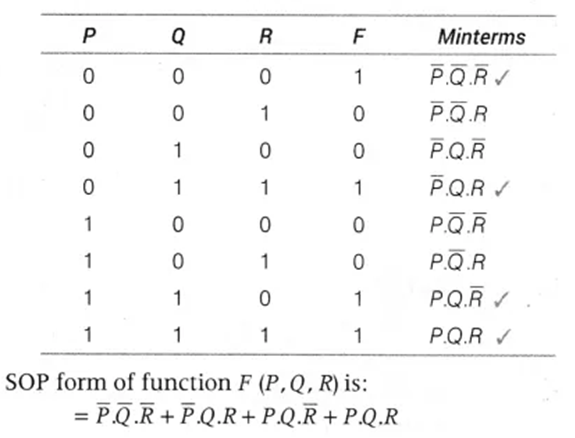
Solution:

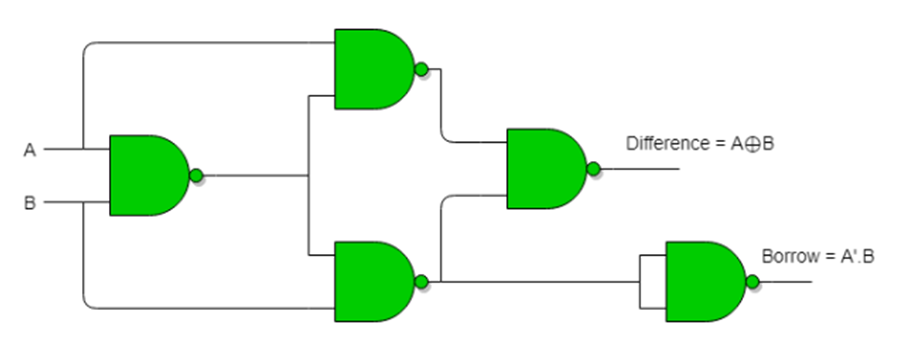
3.     Realize a half subtractor using minimum number of 2-input NAND gates.

4.     What are incompletely specified functions? Simplify the given function using K-Maps:    F= πM (6,7,8,9) .d(10,11,12,13,1,4,15)

An Incompletely specified function is a Boolean function that only define output values for a subset of its inputs - i.e. a Boolean function whose output is a don't care for at least one of its input combinations. Incompletely specified functions often make no guarantees as to the unspecified output whatsoever.

For the given function the K-Map can be drawn as follows:

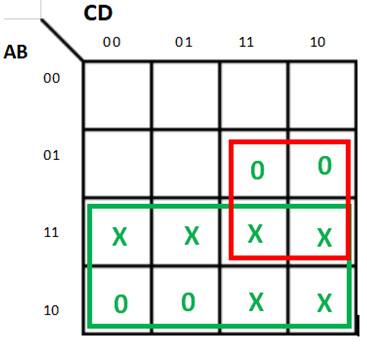
The simplified expression is F= A’ (B’+C’)

5.     How to you get all the possible minimal expressions by the tabular method. Simplify the given expression using the above mentioned method:

F=∑m(0,3,5,6,7,10,12,13)+d(2,9,15)

The Quine–McCluskey algorithm (QMC), also known as the method of prime implicants, is a method used for minimization of Boolean functions.

The Quine–McCluskey algorithm is functionally identical to K-maps, but the tabular form makes it more efficient for use in computer algorithms, and it also gives a deterministic way to check that the minimal form of a Boolean function has been reached. The method involves two steps:

For the given Boolean function, the don’t care terms are treated like required minterms when finding the prime implicants.

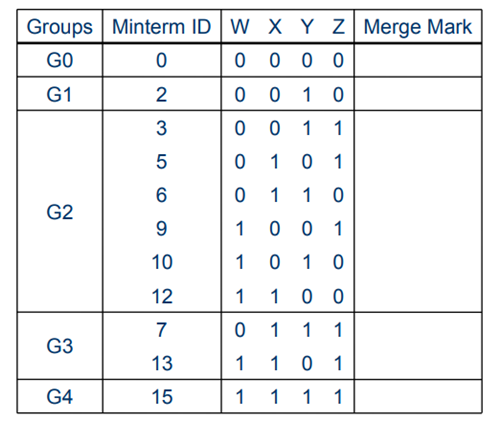
Step 1: Divide all the minterms of the function into groups:

Step 2: Merge the minterms from adjacent groups to form a new implicant table:

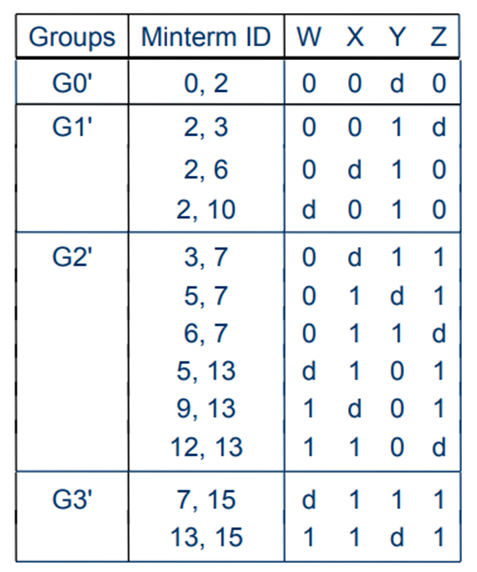
Step 3: Repeat Step 2 until no more merging is possible

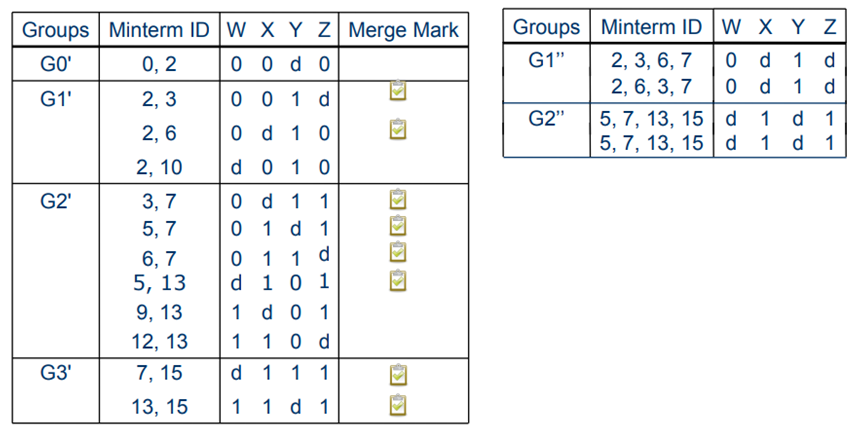
Now, no more merging is possible.

Step 4: Put all the prime implicants in a cover table( don’t cares excluded)

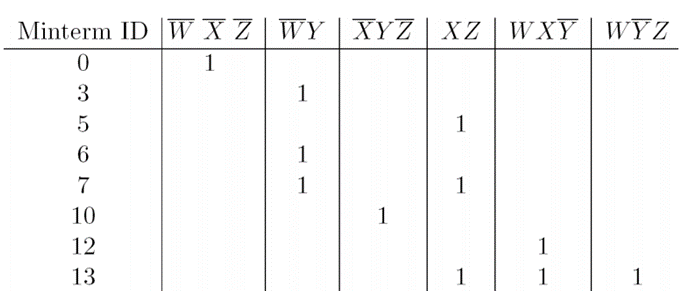
Now identify the essential minterms and hence the essential prime implicants

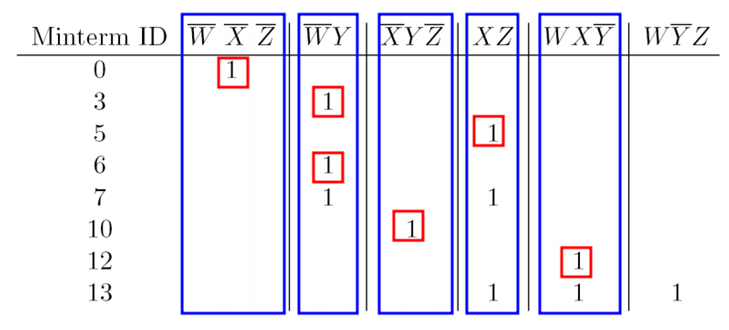
Now, add the prime implicants to the minimum expression of F until all minterms of F are covered.

Thus the simplified expression is: F= W’X’Z’ + W’Y + X’YZ’ + XZ + WXY’

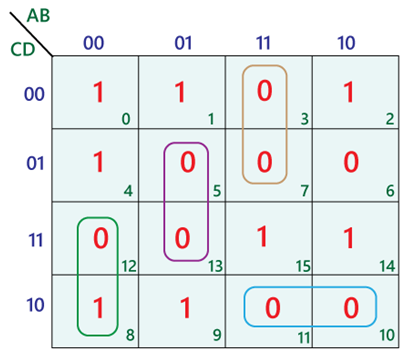
Simplified expression in POS form: Y= (A + C') (A' + B')

Simplified expression in SOP form: Y= A’D’+B’C’D+ABC

7.     Realize a Full-Adder circuit as a combination of two half adders.

The truth table of a Full-Adder circuit is:

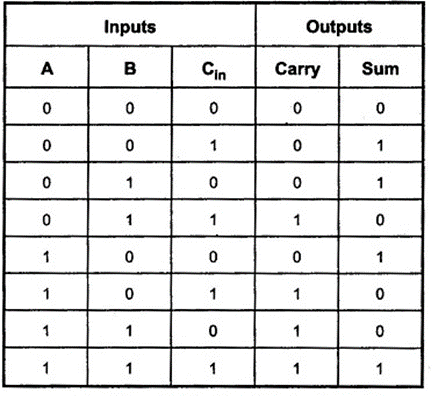
The expression obtained for the outputs using K-Maps are:

Sum= A XOR B XOR C

Cout = AB + Cin (A XOR B)

These expressions can be represented using combination of two half adders and an OR gate as follows:

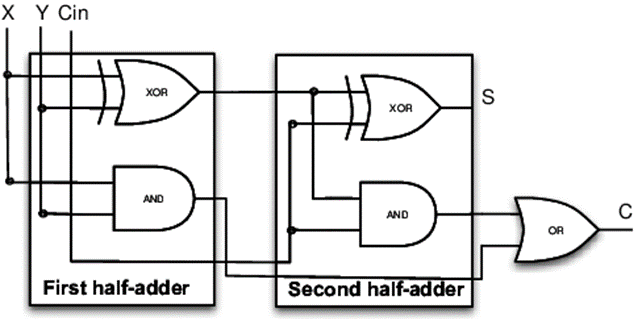
8.     Define maxterms.

A sum term containing all n variables of the function in either true or complemented form is called the maxterm. Each maxterm is obtained by an OR operation of the variables in their true form or complemented form. Four different combinations are possible for a two-variable function, such as, A′ + B′, A′ + B, A + B′, and A + B. These sum terms are called the standard sums or maxterms.

9.     What are code converters? Design a combinational circuit that converts BCD to excess 3 code.

Code converters are logic circuits whose inputs are bit patterns representing numbers or characters in one code and whose outputs are the corresponding representations in a different code.

Truth table for BCD to Excess-3 code conversion:

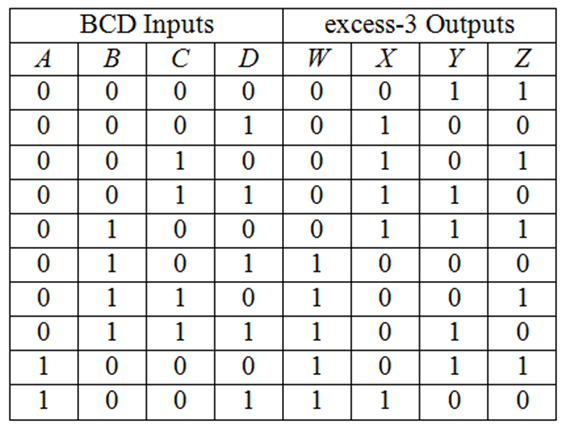
The remaining input combinations result in a don’t care at the output.

The K-Maps can be obtained as follows:

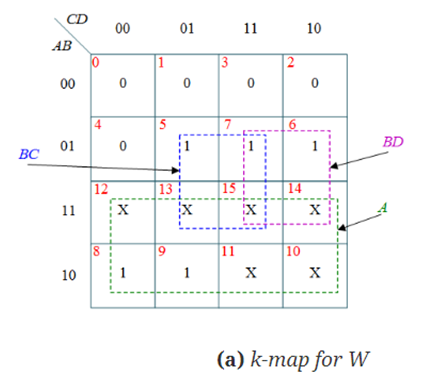
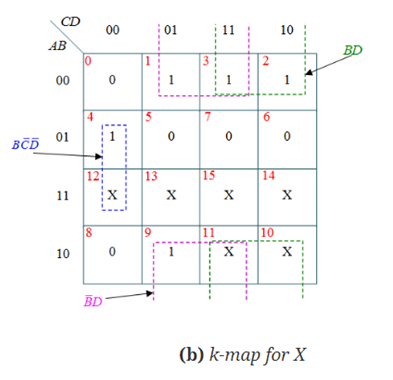
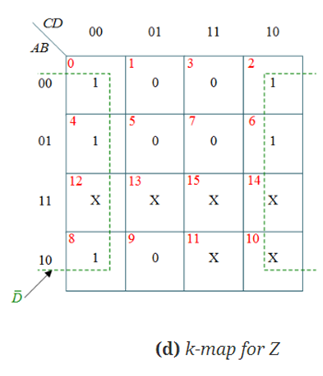
The expressions obtained from the K-map are:

W=A+BC+BD

X=B’C+B’D+BC’D’

Y=CD+C’D’

Z=D’

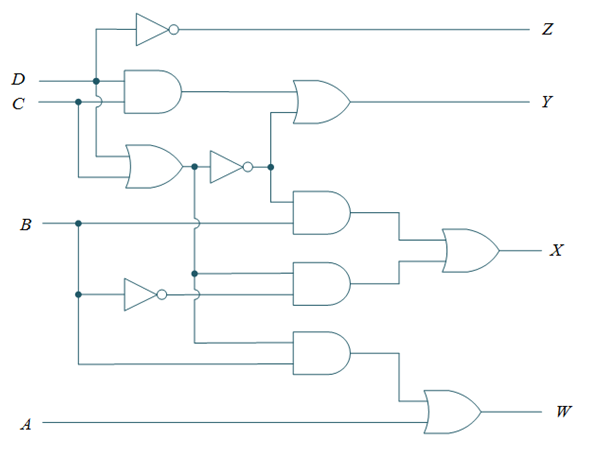
LOGIC CIRCUIT:

10.  How can a SOP expression with don’t cares be converted to a POS form? Expand the function F=   A(B’+A)B   to minterms and maxterms

It can be converted by keeping the don’t cares as they are and writing the missing minterms of the SOP form as the maxterms of the POS form and vice versa.

The given expression is a two variable function in POS form.

F= (A+BB’) (B’+A) (B+AA’)

  = (A+B) (A+B’) (A+B’) (A+B) (A’+B)

  = (A+B) (A+B’) (A’+B)

  = πM (0, 1, 2)

The maxterm M3 is missing in the POS form. So the SOP form will contain only the minterm m3. Thus, F=∑m (3)