undefined | unit 3 combinational circuits

Unit – 3

Combinational Circuits

With the help of an example explain a 4-bit ripple carry adder. What are the disadvantages in using a ripple carry adder?

Using ripple carry adder, this addition is carried out as shown by the following logic diagram-

Let’s take an example of two input sequences 0101 and 1010. These are representing the A4 A3 A2 A1 and B4 B3 B2 B1.

As per this adder concept, input carry is 0.

When A0 & B0 are applied at 1st full adder along with input carry 0.

Here A1 =1 ; B1=0 ; Cin=0

Sum (S1) and carry (C1) will be generated as per the Sum and Carry equations of this adder. As per its theory, the output equation for the Sum = A1⊕B1⊕Cin and Carry = A1B1⊕B1Cin⊕CinA1

As per this equation, for 1st full adder S1 =1 and Carry output i.e., C1=0.

Same like for next input bits A2 and B2, output S2 = 1 and C2 = 0. Here the important point is the second stage full adder gets input carry i.e., C1 which is the output carry of initial stage full adder.

Like this will get the final output sequence (S4 S3 S2 S1) = (1 1 1 1) and Output carry C4 = 0

This is the addition process for 4-bit input sequences when it’s applied to this carry adder.

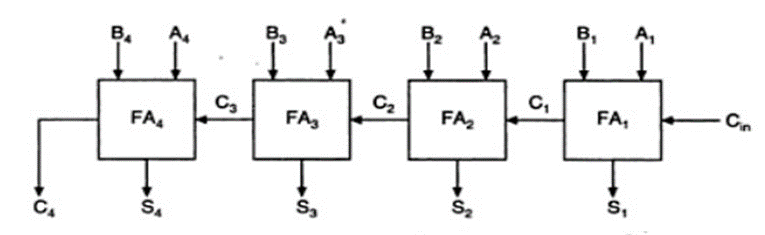
In the ripple carry adder, the output is known after the carry generated by the previous stage is produced. Thus, the sum of the most significant bit is only available after the carry signal has rippled through the adder from the least significant stage to the most significant stage. As a result, the final sum and carry bits will be valid after a considerable delay

2. What is carry look ahead adder? Define the functions CG and CP.

A carry-look ahead adder (CLA) is a type of adder used in digital logic. It improves speed by reducing the amount of time required to determine carry bits. It can be contrasted with the simpler, but usually slower. The carry-look ahead adder calculates one or more carry bits before the sum, which reduces the wait time to calculate the result of the larger value bits.

The output Gi of the first half-adder is 1if Ai and Bi both are 1 and a carry is generated. The variable Gi is known as ‘Carry Generate’ and can be expressed as:

Gi = Ai Bi

The variable Pi known as ‘Carry Propagate’ because a carry in may be propagated by the full-adder when either or both of the input bits are 1. This condition is expressed as the OR function of A and B:

Pi= A+B

3. What is a Parity Bit?

Parity bit is added to the word containing data in order to make number of 1s either even or odd. Thus it is used to detect errors, during the transmission of binary data .The message containing the data bits along with parity bit is transmitted from transmitter node to receiver node. At the receiving end, the number of 1s in the message is counted and if it doesn’t match with the transmitted one, then it means there is an error in the data.

4. Draw the truth table of an odd parity generator circuit. Realize a circuit to implement the same.

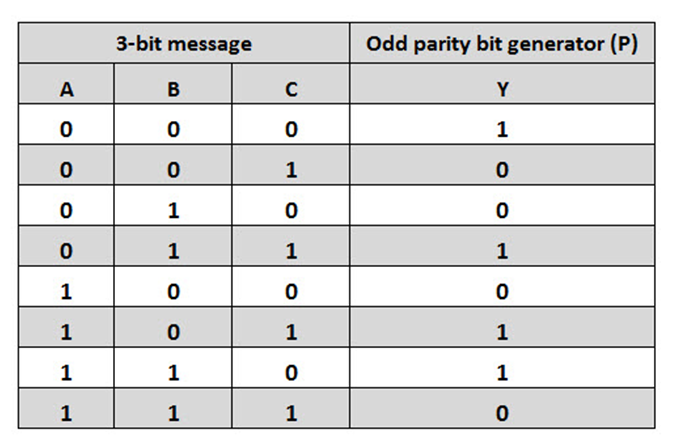
From the truth table, the circuit can be realized as follows:

5. Define a single bit magnitude comparator. Design a 2-bit comparator circuit.

A comparator used to compare two bits, i.e., two numbers each of single bit is called a single bit comparator. It consists of two inputs for allowing two single bit numbers and three outputs to generate less than, equal and greater than comparison outputs.

2 bit comparator:

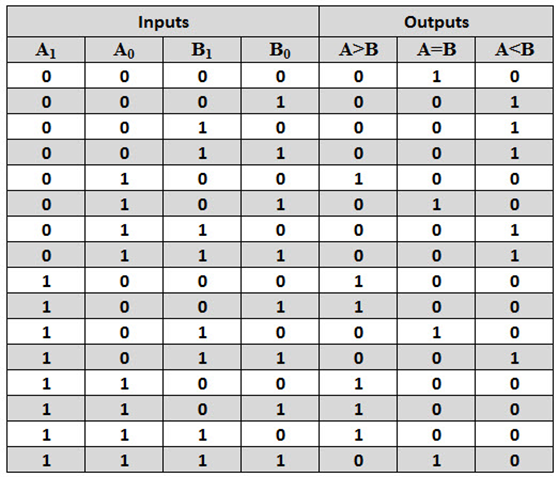
Using K-Maps we get the following equations:

A>B = A1B1′ + B0′ (A0B1′ + A0A1)

A<B = B1A1′ + B0B1A0′ + A1’A0’B0

A=B =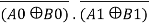

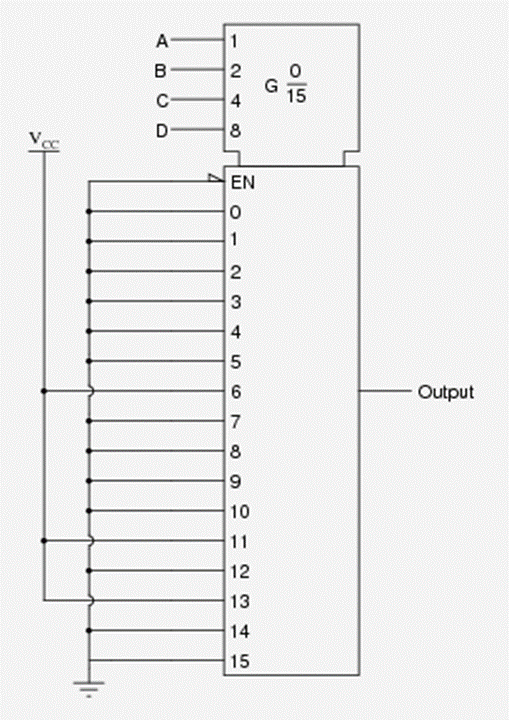
6. Consider the Boolean SOP expression, AB’CD+ABC’D+A’BCD’ for a 16-channel multiplexer. Show the wire connections necessary to make the multiplexer output the specified logic states in response to the data select (A, B, C, and D) inputs.

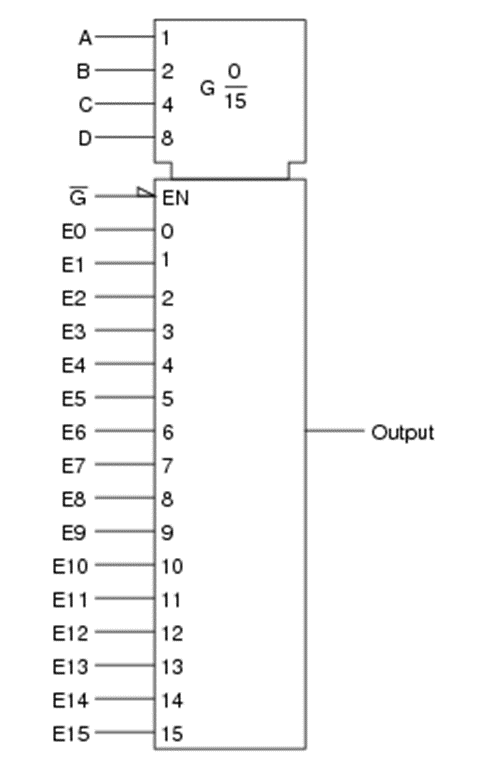
Solution:

The minterms present in the expression should be connected to VCC. Rest of the inputs will be connected to ground.

7. The following schematic diagram is for a two-input selector circuit, which (as the name implies) selects one of two inputs to be sent to the output. Determine what state the “select control” input line has to be in to select input A to be sent to the output, and what state it has to be in to select Input B to go to the output.

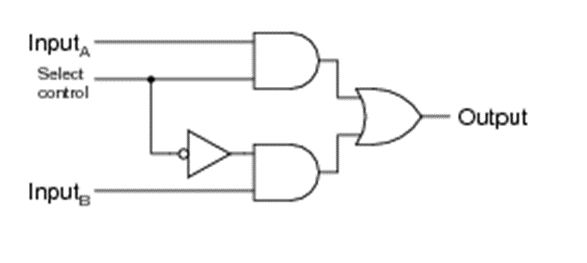
A high signal on the select control line selects Input A , while a low signal on that same line selects Input B.

8. What is a demultiplexer? Realize a Full Subtractor circuit using DEMUX.

A demultiplexer is a combinational circuit that performs the opposite function as that of a multiplexer. In a DEMUX, we have n output lines, one input line, and m select lines. The relation between the number of output lines and the number of select lines is the same as we saw in a multiplexer. That is, 2^m = n. Depending on the value of the binary number formed by the select lines, any one of the output lines connects to the input line.

The rest of the output lines at this point go to an OFF state. That is, the value of the remaining lines is 0. In this way, a demultiplexer converts serial data to parallel data and acts as a serial-parallel converter.

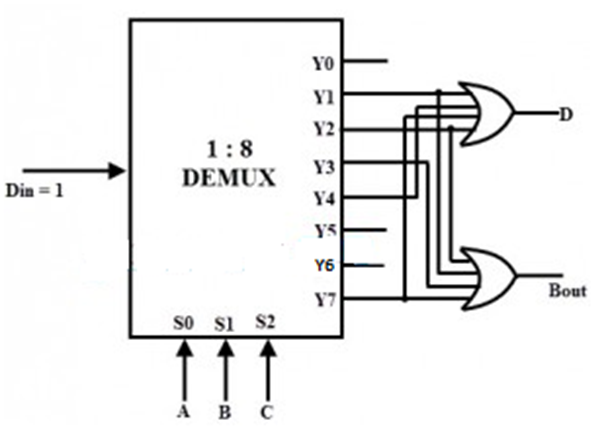
9. What are applications of a DEMUX?

In a communication system, a demultiplexer can receive serial data from a multiplexer that is present at the transmission end. The demux then converts the data into its original form.

We can store an ALU’s output in multiple memory registers using a demultiplexer.

The demultiplexer also acts as a serial to parallel converter.

10. What is the difference between decoder and demultiplexer?

Sign Up