Unit – 1
Q 1:Solve the differential equation y’’’+2y’’-y’-2y=0
Solution:
The corresponding characteristic equation is,
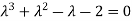
Solving it, we find the roots
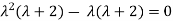
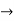

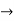
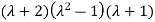 =0
=0
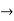
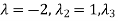 =-1
=-1
The general solution for the differential equation is
Y(x)= 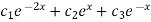
Where 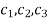 are arbitrary constants.
are arbitrary constants.
Q 2: Solve the equation y’’’+11y’-5y=0
Solution:
The characteristic equation of the give D.E is
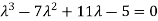
Here one of the root is 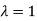 then factorising the term
then factorising the term 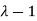 from the equation we obtain
from the equation we obtain
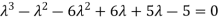
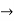 (
(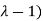 (
(
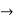 (
(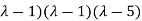 =0
=0
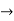 (
(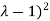 (
(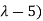 =0
=0
Thus the equation has two roots 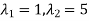
Hence the general equation of the D.E is
Y(x)=(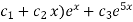
Where 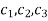 are arbitrary constants.
are arbitrary constants.
Q 3: Determine the complementary function for the following D.E
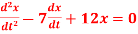 at t=0,1
at t=0,1
Solution:
We can write the given homogeneous equation as follows
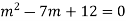
The auxiliary equation is 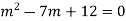
By factorising the auxiliary equations we get,
(m-3)(m-4)=0
And the two real solutions are m=3,4
Hence the complementary function is,
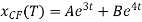
Since f(t) = 2 then 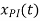 = c
= c
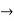 12c=2
12c=2
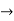 c=1/6 and
c=1/6 and 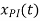 = 1/6
= 1/6
Therefore the general solution is
X(t) = 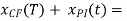
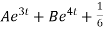
Q 4: Solve 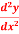 -
-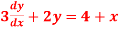
Given y=4 ,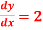 when x=0
when x=0
Solution :
The auxiliary equation is
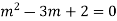
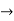 (m-1)(m-2)=0
(m-1)(m-2)=0
 m=1,2
m=1,2
Therefore complimentary function is,

The particular integral is given by y=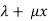

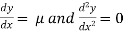
Substituting the above values in given equation we get,
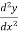 -
-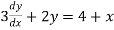 = 0-3
= 0-3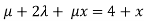
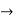 by comparing the co-efficients we get 2
by comparing the co-efficients we get 2 =1
=1 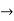
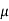 = ½
= ½
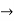 -3
-3 + 2
+ 2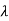 = 4+x
= 4+x
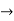
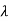 = 11/4
= 11/4
Therefore P.I is,
11/4+(1/2)x
General solution is, y = A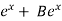 + 11/4 +1/2x
+ 11/4 +1/2x
Q 5: Solve the following linear equations generally
 9x+2y=6 9x+2y=6
9x+2y=6 9x+2y=6
3x-y=7 6x-2y=14
6x-2y=14
Solving the above two equations we get,
9x+2y=6
 6x-2y=14
6x-2y=14
15x = 20
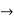 x= 20/15 = 4/3
x= 20/15 = 4/3
Q 6: Short cut methods:
(1) 2x-a+4=x+3a-1
Solution: 2x-x=3a-1+a-4 (-a+4 moves to right side)
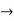 x= 4a – 5
x= 4a – 5
(2) 5x-7=2x+5
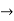 3x = 12
3x = 12 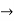 x= 12/3=4
x= 12/3=4
(3) X-m+3=2m+1
Solution: x= 2m+1+m-3= 3m-2 (-m and +3 to right side)
Q 7 : find the particular integral for the following

Solution:
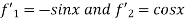
Now the C.F is as follow,
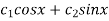
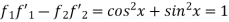
We find u and v accordingly

= -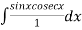 = -x
= -x
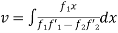
= 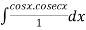 = log(sinx)
= log(sinx)
P.I = 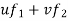
= -xcosx +log(sinx)
The general solution is y = C.F +P.I
Y = 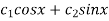 -xcosx +log(sinx)
-xcosx +log(sinx)
Q 8: Wronskain ,W= 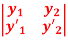
=  =
= 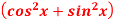 =1
=1
Particular integral is given by,
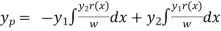

 secx= 1/cosx
secx= 1/cosx

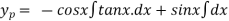
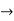

The general solution is,
Y = C.F +P.I
Y = 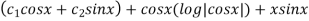
Q 9: Check the validity for cauchy’s mean value theorem f(x) = 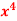 and g(x) =
and g(x) = 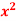 on the interval [1,2]
on the interval [1,2]
Solution:
The derivatives of this function are,
f’(x) = (x4) = 4x3, g’(x)=(x2) = 2x
substituting in the Cauchy formula we get,
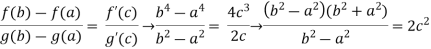
We take into account that the boundaries of the segment are a=1 and b=2
C=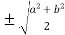
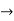 c=
c=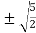 =
=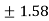
Q 10: Check the validity for cauchy’s theorem for the function f(x) = x2 and g(x) = arctanx on the interval [0,1]
Solution:
At first we calculate the derivatives of the given function
f’(x) = (x3)’ , g’(x) = (arctanx)’= 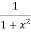
substitute f(x),g(x) and their derivatives in the Cauchy formula
 =
= 
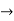
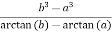 =
= 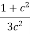
For the values of a=0, b=1 we obtain,



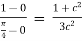
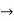
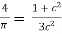
 12c2 =
12c2 = 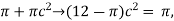

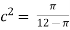
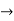 c =
c = 
Given we consider the segment [0,1],we choose the positive value for c which lies in interval(0,1)
C=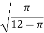
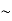
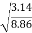
 0.60
0.60
Legendre’s formul:
 =
= 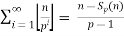
Where p is a prime and 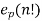 is the exponent of p in the prime factorizatio of n! And sp(n) is the sum of the digits of n when written in bas p
is the exponent of p in the prime factorizatio of n! And sp(n) is the sum of the digits of n when written in bas p
Q 11: Using the first form of Legendre’s equation , substitute the values in the formula
The values are n=27 and p =2
Solution :
Consider the Legendre’s formula,
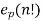 =
= 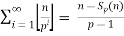
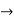 substituting the given values in the formula we get,
substituting the given values in the formula we get,
 =
= 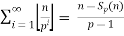 =
= 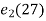 =
= 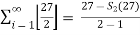 = 27 – s2(27)
= 27 – s2(27)
 the number 27 when expressed in the base 2 gives rise to 11011.this gives us,
the number 27 when expressed in the base 2 gives rise to 11011.this gives us,
s2(27) = 1+1+0+1+1 = 4

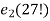 = 27 – s2(27) = 27 – 4 =23
= 27 – s2(27) = 27 – 4 =23
Which means that the larget integer k for which 2k divides 27! Is 23.
Q 12:
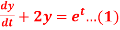
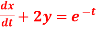 ....(2)
....(2)
Solve the given simultaneous differential equations
Solution:
Consider the given equations
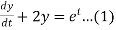
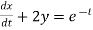 ....(2)
....(2)
Consider eq(1),(2)
Dx+2y = et ....(1)
Dx +2x =e-t....(2)
Eliminating ‘x’ from both the equations we get,
1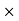 2
2 2Dx + 2y = 2et
2Dx + 2y = 2et

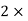 D
D  2Dx +D2y = e-t
2Dx +D2y = e-t

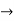 y = Ae2t + Be-2t +
y = Ae2t + Be-2t + 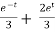
Q 13:

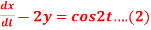
Given that x(0)=1 and y(0)= 0
Solution:
Consider the given equations,
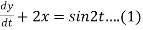
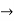 Dy +2x = sin2t
Dy +2x = sin2t

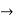 Dx -2y = cos2t
Dx -2y = cos2t
By solving the above equations we get,
(D2 +4)Y =0


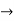

X(0) = 1, y(0) = 0
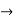 A =0, B=-1
A =0, B=-1

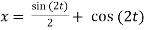
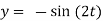
Q 14: Finding the optimal current of an electrical circuit(RL circuits) in which the initial Condition is i=0 at t=0

Solution:
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be 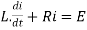
In which initial conditions are i=0 at t=0
The standard form of the equation is,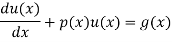
Dividing the differential equation by L to obtain
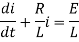
The integrating factor is
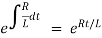
Multiplying the above equation with standard form gives rise to
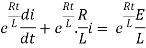

By applying integration on both sides we get
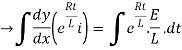
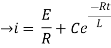
Now applying i=0 at t-0 gives us
0=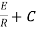
 C=-
C=-
NOW
i=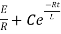
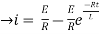
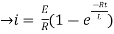 = t
= t 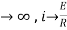
Therefore by finding current of the RL circuits is i=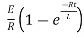
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.