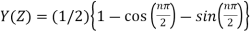UNIT-2

Q1:

Using complex form,find the Fourier series of the function

 f(x) = signx =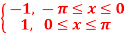

solution:

we calculate the coefficients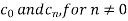

  =

=

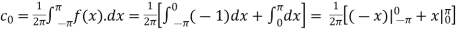
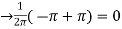
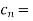
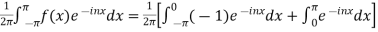
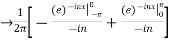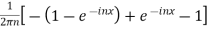
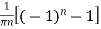
Hence the Fourier series of the function in complex form is

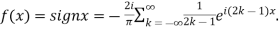
We can transform the series and write it in the real form by renaming as

 n=2k-1,n=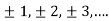

                                    =

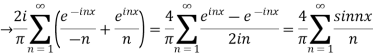
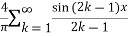
Q2:

Using  complex form find the Fourier series of the function f(x) = x2, defined on te interval [-1,1]

Solution:

Here the half-period is L=1.Therefore,the co-efficient c0  is,

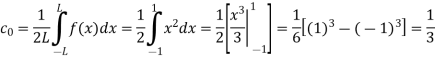
For n

Integrating by parts twice,we obtain

=

=

= .

= .

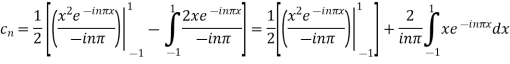
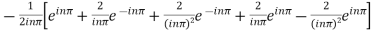
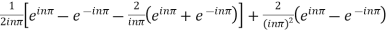
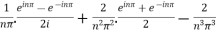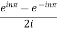
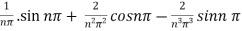Q3

Find the fourier integral representation of the function

Solution:

The graph of the function is shown in the below figure  satisfies the hypothesis of

Theorem -1 . Hence from Eqn,(5) and (6), we have

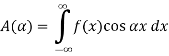
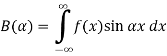
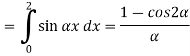
Substituting these coefficients in Eqn.(4) we obtain

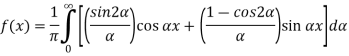
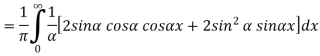
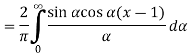
This is the Fourier integral representation of the given function.

Q 4:

Find the Fourier integral representation of the function

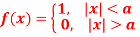
Solution:

The graph of the given function is shown in the below figure . Clearly, the given function f(x) is an even function. We represent  f(x) by the fourier cosine integral . We obtain

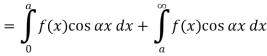
And thus ,       

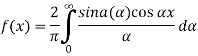
Q 5:

Find the Fourier cosine integral of , where x>0, k>0 hence show that

Solution:

The Fourier cosine integral of f(x) is given by:

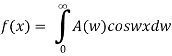
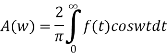
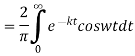
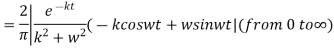
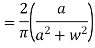
Q 6:

Find the half –range sine series of the function

Solution:

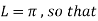
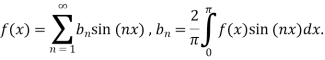
Where

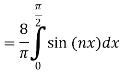
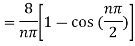
Q7:

Fourier sine integral for even function f(x):

Solution:

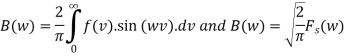
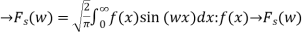is a Fourier sine transform of f(x)

is a Inverse Fourier sine transformation of FC(x)

Q 8:Fourier cosine integral for even function f(x):

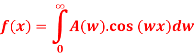
Solution:

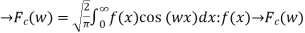Fourier cosine transform of f(x)

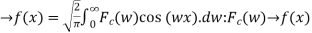...Inverse Fourier cosine transform of Fc(x).

Q 9:

Fourier cosine and sine transforms

Consider,

=

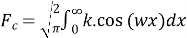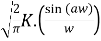
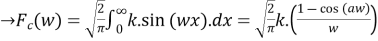
Q 10:

Fourier cosine transformation of the exponential function:

F(x)= ex

Solution:

Given,

F(x)= ex

From the know formula we directly apply,

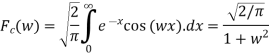
Q 11:

Find the z-transformation of the following left-sided sequence

Solution:

                                                             = 

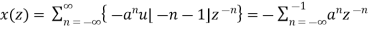
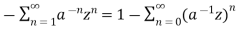
                                                              = 1-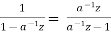

                                                              =

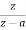
If 

Q 12:

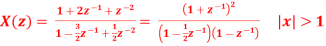
Solution:

Long division method  to obtain

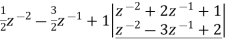2

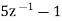
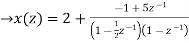
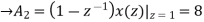
Now x(z) can be written as,

X(z) = 2-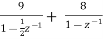

Q 13:

Solve the differential equation 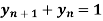 by z-transformation method.

Solution:

Given,

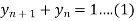
Let y(z) be the z-transform of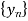

Taking z-transforms of both sides of eq(1) we get,

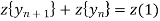
ie.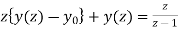

using the given condition ,it reduces to

(z+1)y(z) =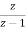

Ie.

Y(z) =

Or Y(Z) =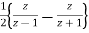

On taking inverse Z-transforms, we obtain

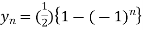
Q 14:

Solve 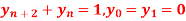using z-transforms

Solution:

Consider,

Taking z-transforms on both sides, we get

=

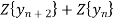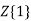
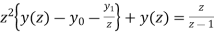
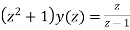   or

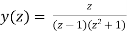
Now,

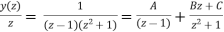
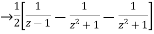
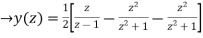
Using inverse z-transform we obtain,