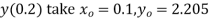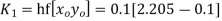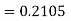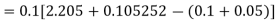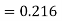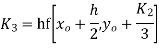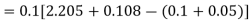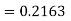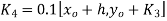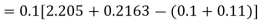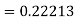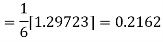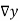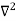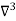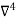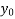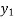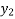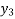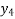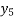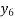Unit 3
Q 1:
Newton Forward differences 
Y( + rh) =
+ rh) = 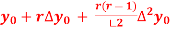 +
+ 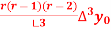 + ….
+ ….
Newton Backward difference 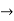
Y(x) = y (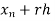 ) =
) = 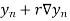 +
+ 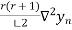 +
+  + …….
+ …….
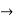 The population of a city in the decimal census is given in the following table
The population of a city in the decimal census is given in the following table
Year X | 1891 | 1901 | 1911 | 1921 | 1931 |
Population Y (in thousand) | 46 | 66 | 81 | 93 | 101 |
Approximate the population of the city in the years 1895 and 1925
SOLUTION:  Difference Table
Difference Table
X | Y |
|
|
|
|
1891 | 46 | 20 |
|
|
|
1901 | 66 | 15 | -5 | -2 |
|
1911 | 81 | 12 | -3 | -1 | -3 |
1921 | 93 | 8 | -4 |
|
|
1931 | 101 |
|
|
|
|
Compute the population in 1895
Using Newton forward differences formula
Y(x) = 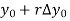 +
+ 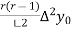 +
+ 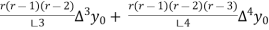 + …
+ …
Let 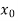 = 1891 h = 10 X =
= 1891 h = 10 X = 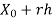 = 1895
= 1895
r = 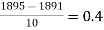
y(1895) = 46 + 0.4(20)+  (-5)+
(-5)+ 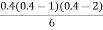 (2) +
(2) + 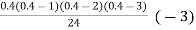
= 54.85 thousand (Approx)
Compute the population in 1925 using backward difference formula
Y(x) = 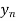 + r
+ r + ……..
+ ……..
Let 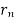 = 1931 r =
= 1931 r = 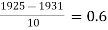
Y(1925) = 101 + (0.6) 8 + 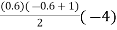 +
+ 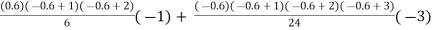
= 96.84 thousand only.
Q 2:
using divided difference interpolation . Find f(x)
x | 0 | 1 | 2 | 4 | 5 | 6 |
Y = f(x) | 1 | 14 | 15 | 5 | 6 | 19 |
 The divided difference table
The divided difference table
x | 4 | d.d of order1 | d.d of order2 | d.d of order3 | d.d of order4 | d.d of order5 |
0 | 1 |
|
|
|
|
|
1 | 14 | 13 | -6 | 1 |
|
|
2 | 15 | 1 | -2 | 1 | 0 |
|
3 | 5 | -5 | 2 | 1 | 0 | 0 |
4 | 6 | 1 | 6 |
|
|
|
5 |
| 13 |
|
|
|
|
6 | 19 |
|
|
|
|
|
Using formula
Y = f(x)=  + (x -
+ (x - 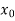 )
)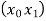 + (x -
+ (x - 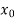 ) (x-
) (x- 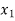 )f
)f + (x -
+ (x - 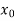 )(x -
)(x - 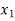 )(x -
)(x - 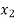 ) f
) f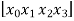 +…….
+…….
= 1 + (x - 0)(13) + (x - 0)(x-1)(-6)+ (x - 0)(x-1)(x -2)(1) + (x -0)(x-1)(x - 2)(x - 4)(0) + (x -0)(x - 1)(x -1) (x - 2)(x - 4)(x -5)0+ 0
= 1 + 13x + ( - x)(-6)+ (
- x)(-6)+ (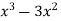 + 2x)(1) + 0
+ 2x)(1) + 0
= 1 + 21x - 9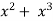
f(x) = 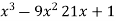
Q3:
Using Lagranye’s interpolation Solve the following data
x | 300 | 304 | 305 | 307 |
| 2.477 | 2.482 | 2.484 | 2.487 |
Calculate the approximate value of 
Solution:
Using formula
y = 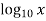 =
= 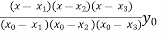 +
+ 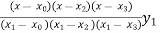 +
+ 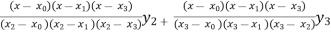
= 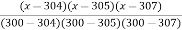 (2.477) +
(2.477) + 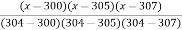 (2.482) +
(2.482) + 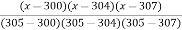 (2.484) +
(2.484) +  (2.4871)
(2.4871)
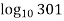 =
= 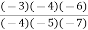 (2.477) +
(2.477) +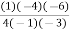 (2.4829) +
(2.4829) + 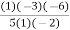 (2.4843) +
(2.4843) + 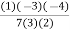 (2.4871)
(2.4871)
= 1.2739 + 4.9658 – 4.4717 + 0.7106
= 2.4786
Q 4:
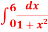 by (i) Trapezoidal rule , (ii) Simpson’s
by (i) Trapezoidal rule , (ii) Simpson’s  rule ,(iii) Simpson’s
rule ,(iii) Simpson’s  rule
rule
Solution  Let h = 1 or Let n = 6
Let h = 1 or Let n = 6
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
f(x) = | 1 | 0.500 | 0.200 | 0.100 | 0.05 | 0.038 | 0.027 |
|
|
|
|
|
|
|
|
By Trapezoidal rule
I = 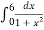 = h
= h 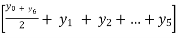
= 1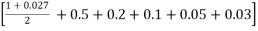
= 1.41
By Simpson’s rule
I = 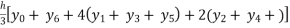
= 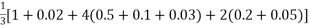
= 1.366
Simpson’s  rule
rule 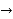
I = 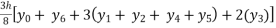
= 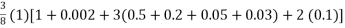
= 1.357
Q 5:
maclurian series ln(1+x)
S = 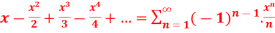 (-1 < x
(-1 < x  1)
1)
Solution:
Consider the given maclurian series is ln(1+x)
And assume n=5
S = 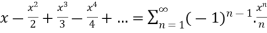 (-1 < x
(-1 < x 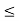 1)
1)
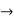 s = 1-
s = 1- 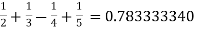
In 2 = 0.693
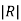 =
=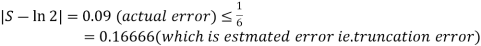
Q 6:
Estimate the truncation error if we calculate e as 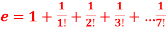
Solution:
Given 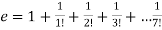
This is the maclurian series of f(x) = ex with x=1 and n=7.
Thus the bound of the truncation error is

Therefore the actual truncation error is about 0.2786 
Q 7:
How many terms are required in calculation of 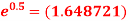 using a maclurian series expansion,in which the result is correct to atleast 3 significant figure.
using a maclurian series expansion,in which the result is correct to atleast 3 significant figure.
Solution:
Considering the maclurian series

Finding of error for 3 significant values is,
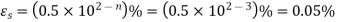
Q 8:
Using Runge kutta method of fourth order determine y (0.1) and y(0.2) correct to four decimal place given that 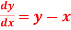 where y(0)=2 and h=0.1.
where y(0)=2 and h=0.1.
Solution:

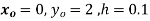
To find y(0.1) we have
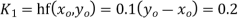
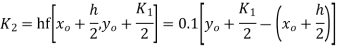
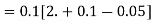
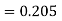
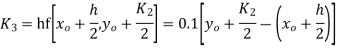
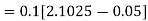
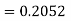
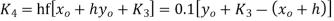
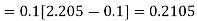
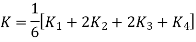
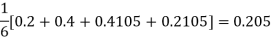

For