UNIT-6
Q1:
Solve the following complex function:
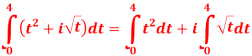
Solution:
Given,
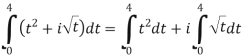
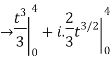
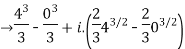
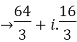
Q 2:
Using the residue theorem to evaluate:
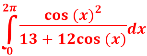
Solution:
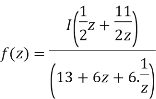
The singularity z=0,is in our region and we will add the following residue
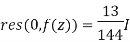
The singularity z = -3/2 will be skipped because the singularity is not in our region.
The singularity z= -2/3 is in our region and we will add the following residue
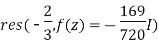
Our sum is,
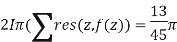
Therefore the solution is,
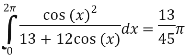
Q 5:
Prove that the function 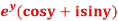 is an analytical function.
is an analytical function.
Solution. Let 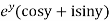 =u+iv
=u+iv
Let 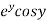 =u and
=u and 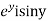 =v
=v
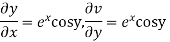

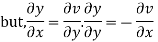
Hence e-R-Equation satisfied.
Prove that 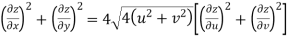
Answer Given that
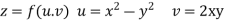
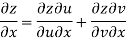
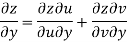
Since 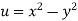

V=2xy

Now 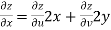
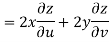
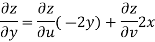
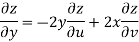
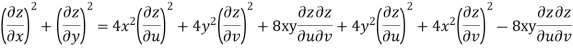
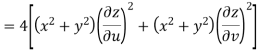
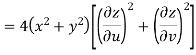
But 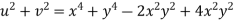
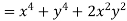
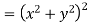
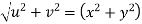
Hence 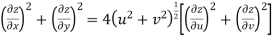
Q 6:
Find the bi-linear transformation which aps points z=2,1,0 ontpo the points w=1,0,i
Solution:
Let 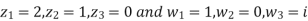
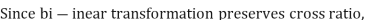
Thus we have
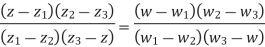
= 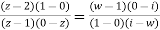
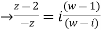

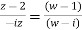
Q 7:
How that the bi-liear transformation w= 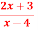 transforms
transforms 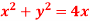 in the z-plane to 4u+3=0 in w-plane.
in the z-plane to 4u+3=0 in w-plane.
Solution:
Consider  the circle in z-plane
the circle in z-plane

 = 0
= 0
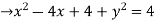

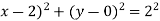
Thus,centre of the circle is (h,k) c(2,0) and radius r=2.
c(2,0) and radius r=2.
Thus in z-plane it is given as 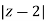 =2....(1)
=2....(1)
Consider w= 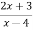
W(z-4) = 2z+3
Wz-4w=2z+3
Wz-2z=4w+3
Z(w-2) = (4w+3)
 z =
z = 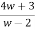
z-2 = 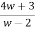 - 2
- 2

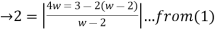

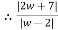
Q 8:
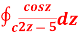 where C =
where C = 
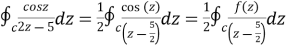 where f(z) = cosz
where f(z) = cosz
= 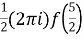 by cauchy’s integral formula
by cauchy’s integral formula
= 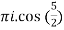
Q 9:
Solve the following by cauchy’s integral method:
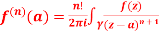
Solution:
Given,
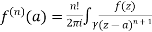

= 
= 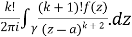
= 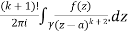
Q 10:
Evaluate the following integral using residue theorem
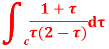
where c is the circle.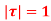 .
.
Ans. The poles of the integral are given by putting the denominator equal to zero
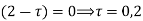
The integral is analytic on 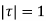 and all points inside except
and all points inside except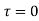 as a pole at
as a pole at 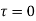 is inside the circle
is inside the circle 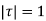
Hence by residue theorem
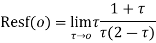
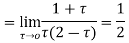
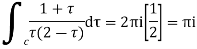
Q 11:
Evaluate 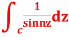 where c;|z|=4
where c;|z|=4
Answer Here f(z)=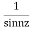
Poles are 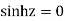
Sin iz=0
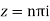
Poles 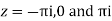
Lie inside the circle |z|=4
The given function 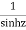 is of the form
is of the form 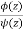
Its pole at z=a is 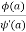
Residue (at 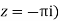
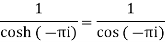
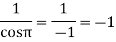
Residue at z=0=
Residue at 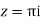 =
=
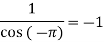
Residue at 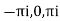 are
are
Respectively -1,1 and -1
Hence the required integrand

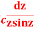
Answer 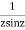 =
=
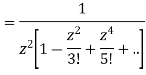
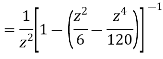

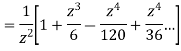
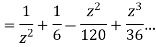
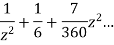
This shows that z=0 is a pole of order 2 for the function 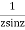 and the residue of the poles is zero(coefficient of 1/z)
and the residue of the poles is zero(coefficient of 1/z)
Now the pole at z=0 lies within c
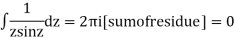
2. Evaluation of definite integrand
Show that 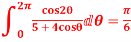
Solution I= 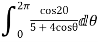
Real part of 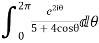
Now I= 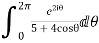 =
=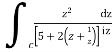
Putting z= where c is the unit circle |z|=1
where c is the unit circle |z|=1
I=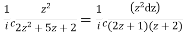
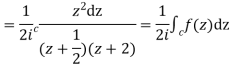
Now f(z) has simple poles at 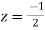 and z=-2 of which only
and z=-2 of which only 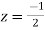 lies inside c.
lies inside c.
Residue at 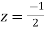 is
is 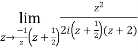
=
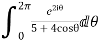 =
=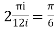
Now equating real parts on both sides we get
I=
3. Prove that 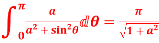
Solution Let 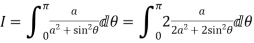
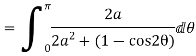

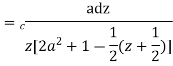
Putting 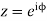 where c is the unit circle |z|=1
where c is the unit circle |z|=1

2ai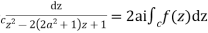
Poles of f(z) are given by the roots of
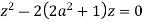
Or 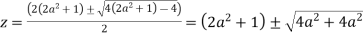
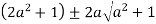
Let 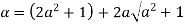

Clearly 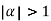 and since
and since 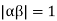 we have
we have 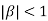 Hence the only pole inside c is at z=
Hence the only pole inside c is at z=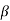
Residue (at 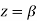 )
)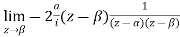
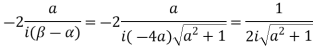
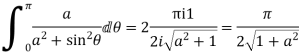
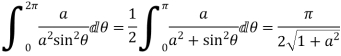
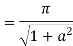
4. Evaluate 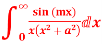
Answer Consider 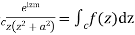
Where c is the closed contour consisting of
1) Real axis from 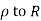
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to 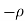 and
and
4) Small semicircle given by |z|=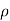
Now f(z) has simple poles at z=0  of which only z=
of which only z=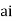 is avoided by indentation
is avoided by indentation
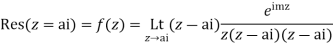
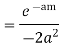
Hence by Cauchy’s Residue theorem
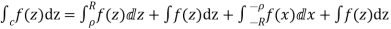
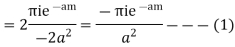
Since 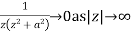 and
and
Hence by Jordan’s Lemma 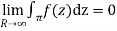
Also since 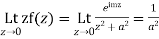
Hence 
Hence as 
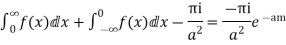
Equating imaginary parts we get

Q 12:
Prove that 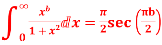
Solution Consider 
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of 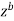 by indenting the origin
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue(at z=i) =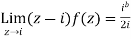
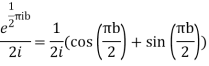
Hence by residue theorem
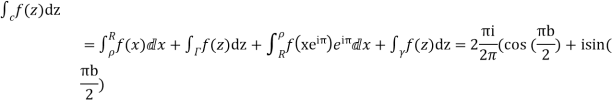
Since 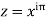 on -ve real axis.
on -ve real axis.
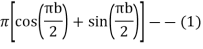
Now 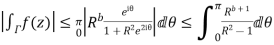
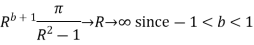
Similarly 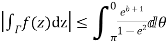
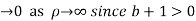
Hence when 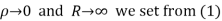
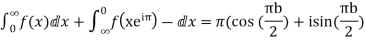

Equating real parts we get

