Unit V

State Space Representation

Q1 Obtatin the state space representation for the given electircal system

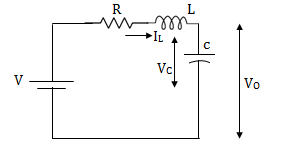
Fig 1 Electrical circuit

Solution: The state model is given as

Fig 2 State model

The state model shows that there are two energy storing elements L, C. As we already know that Number of state variables is equal to the number of energy storing elements.Hence we have two state variables[x1(t) and x2(t)]. We have one output V0(taken across capacitor) and input u(t).

The output equation is then given as

Y(t)=CX(t)+DU(t)

V0=Vc= x1(t)                                                              ….(a)

Hence output equation becomes

V0= x1(t)

y(t)=[1   0]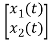+[0]u(t)

So, C=[1   0]       D=[0]

Now writing the state equation

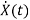=Ax(t)+Bu(t)

For that applying KVL in the above circuit

V=ILR+L+Vc

State Equation is 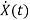=Ax(t)+Bu(t)

=

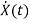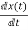
x1(t)=Vc

=

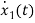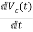
IL=C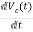

=

==

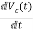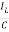
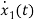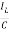
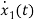=(1/C) x2(t)                                                          ……….(b)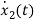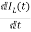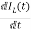

==

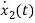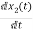VL=L

==VL/L

From KVL

L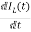=VL=V-ILR-VC

==

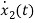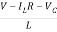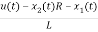
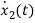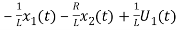=                                 …………….(c)

From equation (b) and (c)

= [0         1/c]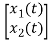+ [0  0]u(t)

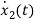=[-1/L         -R/L] 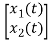+ [1/L       0]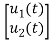

Now writing the state equation

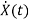=Ax(t)+Bu(t)

=+

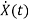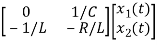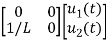
Hence A=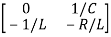        B=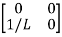

Q2 Obtatin the state space representation for the given electircal system

Fig 3 Electrical circuit

Solution: The state model shows that there are two energy storing elements L, C. As we already know that Number of state variables is equal to the number of energy storing elements.Hence we have two state variables[x1(t) and x2(t)]. We have one output V0(taken across capacitor) and input u(t).

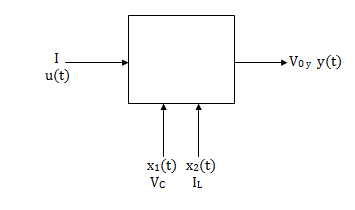
Fig 4 State Model

Here output is V0. But from above electrical circuit V0=ILR

V0=x2(t)R

y(t)= V0= [0      R] 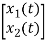+ [0] u(t)

The output equation is given as

Y(t)=CX(t)+DU(t)

C=[0    R]      D=[0]

Now finding state equation,we apply KCL in the given electrical circuit

I=IC+IL

=

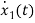But I-IL=IC

=

=

 =

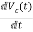
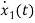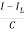
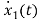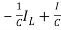
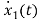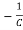 =x2(t)+ 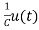                                     ……..(a)

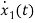=[0      1/C]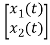+ [1/C      0] 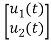      …….(b)

==

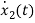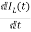
Applying KVL in the given electrical circuit we get

VC=VL+ILR

VC-ILR=VL=L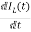

=     

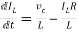
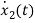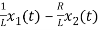
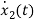=[1/L    -R/L] 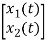+ [0] u(t)    ………….(c)

From equation (b) and (c) we have

Now writing the state equation

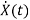=Ax(t)+Bu(t)

=+

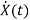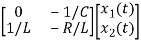Hence A=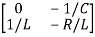        B=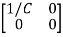

Q3 Find the observable canonical realization of the system H(s)=

Solution: The above transfer function can be also written as

H(s)=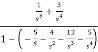

Comparing above equation with standard equation we conclude that

The gains of forward paths are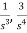 

The feedback loop gains are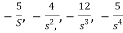 

The SFG satisfying above conditions will be

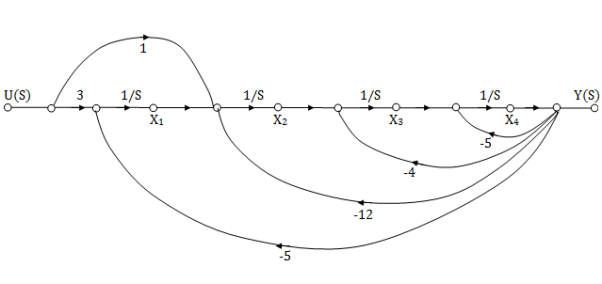
Fig 5 SFG for observable canonical form

The observable canonical form can be obtained by converting the above SFG to block diagram

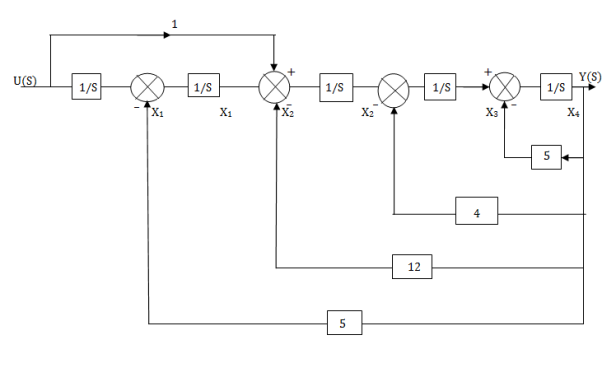
Fig 6 Block diagram for observable canonical form

Q4 Find the controllable canonical realization of the following systems

H(s)=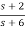

Solution: H(s)=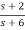

Let H(s)=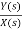

=

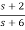
H1(s)=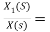1/s+6

X(s)=sX1(s)+6X1(s)

SX1(s)= X(s) +6X1(s)

We can get X1(s) by passing sX1(s) through integrator. The above equation can be realised as

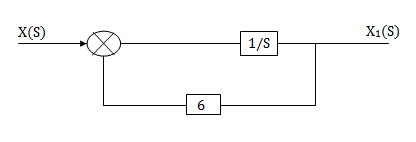
Fig 7 Block diagram for H1(s)=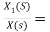1/s+6

H2(s)=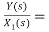s+2

Similarly, Y(s)= sX1(s)+2X1(s)

H2(s)=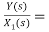s+2

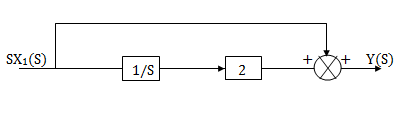
Fig 8 Block diagram for H2(s)=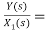s+2

The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be

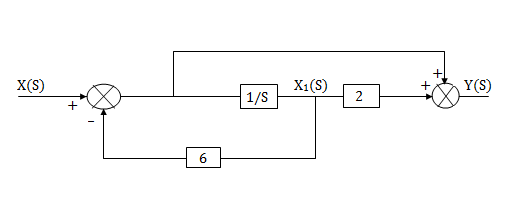
Fig 9 Complete Block diagram

Q5 Find the controllable canonical realization of the following systems

H(s)=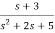

Sol: Let H(s)=  =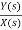

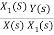
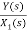      =s+3

Y(s)=sX1(s)+3X1(s)

The above transfer function can be realised as

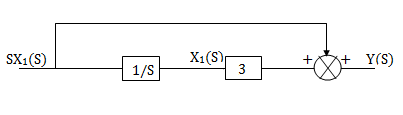
Fig 10 Block diagram for s+3

Now, =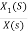

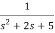
s2X1(s)=X(s)-2sX1(s)-5X1(s)

Assuming s2X1(s) is available the above transfer function can be realised as

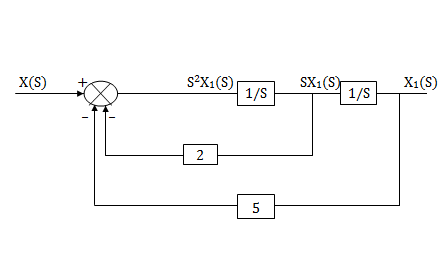
Fig 11 Block Diagram for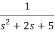

The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be

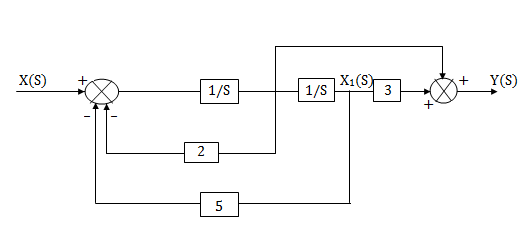
Fig 11 Final Block Diagram

Q6 A=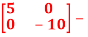. Find the state transition matrix?

Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)

[SI-A]= -

           =-

           =

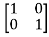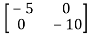
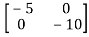
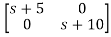
Taking inverse Laplace of above, we get

[SI-A]-1=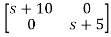/(S+5)(S+10)

             =

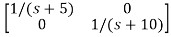
Hence φ(t)=L-1[SI-A]-1=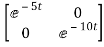

Q7 Find state transition matrix if A=

Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)

[SI-A]=-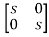

            =

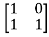
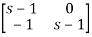
[SI-A]-1=

Hence φ(t)=L-1[SI-A]-1=

Q8) A=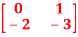 . Calculate characteristic equation and stability?

Sol: The characteristic equation is given as [SI-A]=0

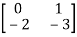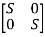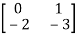S - =0

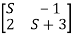- = 0

=0

S(S+3)-(-1)*2=0

Hence, the characteristic equation is

S2+3S+2=0

(S+1)(S+2)=0

S=-1,-2

Both roots on left-half of s-plane, real and different, system absolutely stable.

Q.9) A= 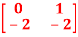Find the characteristic equation and comment on stability?

Sol: The characteristic equation is given by [SI-A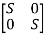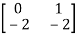]=0

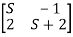-=0

=0

S(S+2)+2=0

S2+2S+2=0

S=-1±j

Roots on left-half of s-plane, complex conjugate, system absolutely stable.

Q10) List the properties of state transition matrix?

Sol:

Property 1:

φ(0)= [I]

Property 2:

Φ-1(t)= [φ(t)]-1=e-At=eA(-t)

Φ-1(t)= Φ(-t)

Property 3:

ΦK(t)= [Φ(t)]K

ΦK(t)=[eAt]K=eA(tK)

ΦK(t)= Φ(Kt)

Property 4:

Φ(t1+t2)=eA(t1+t2)

                    =e(At1+At2)=eAt1 * eAt2

Φ(t1+t2)= Φ(t1)Φ(t2)

Property 5:

Φ(t2-t1) * φ(t1-t0)=eA(t2-t1) * eA(t1-t0)

                                           =

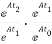
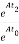                           ==eA(t2-t0)

Φ(t2-t1) * φ(t1-t0)= Φ(t2-t0)