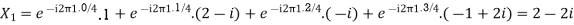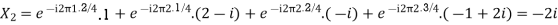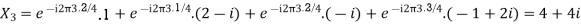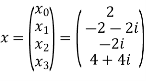Unit - 3
Transforms (DFT-FFT)
Q1) Find circular convolution using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
A1)
Circular convolution using circular convolution:
x1x1(n) = {1, 2, 3, 4}
And x2x2 (n) = {1, 2, 1, 2}
L=4, M=4
Length of y(n) = L+M-1=4+4-1=7
∴,x1(n) = {1, 2, 3, 4, 0, 0, 0}
& x2(n) = {1, 2, 1, 2, 0, 0, 0}
For y(0),
∴ y(0)= 1×1=1
For y(1),
∴ y(1)= 2×1+1×2=4
For y(2),
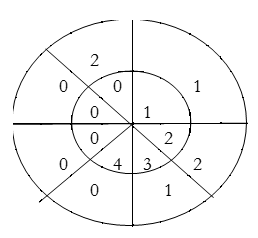
∴ y(2)= 1×1+2×2+3×1=8
For y(3),
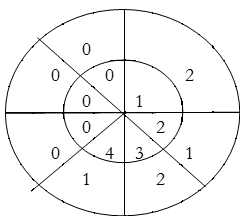
y(3)=1×2+2×1+3×2+4×1=14
For y(4),
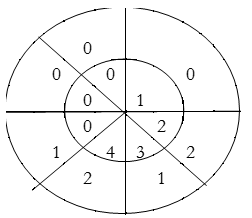
∴ y(4)= 4×2+3×1+2×2=15
For y(5),
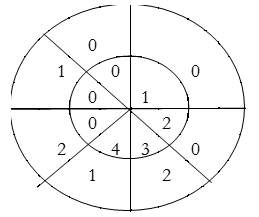
∴ y(5) = 4×1+3×2=10
For y(6),
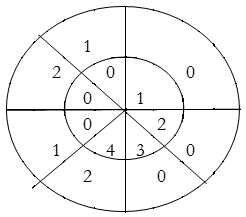
∴ y(6) = 4×2=8
∴y(n) = {1, 4, 8, 14, 15, 10, 8}
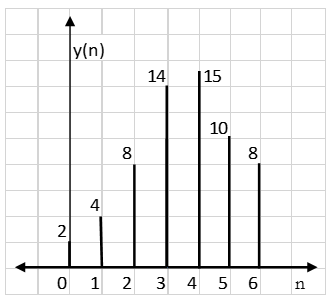
Result: y(n) = {2, 4, 8, 14, 15, 10, 8}
Q2) Find circular convolution using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
A2) Linear using circular convolution:
For y(0),
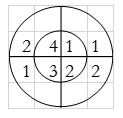
∴ y(0)= 1+4+3+8=16
For y(1),

∴ y(1)= 2+2+6+4=14
For y(2),

∴ y(2)= 1+4+3+8=16
For y(3),
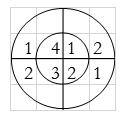
∴ y(3)= 2+2+6+4=14
y(n) = {16, 14, 16, 14}
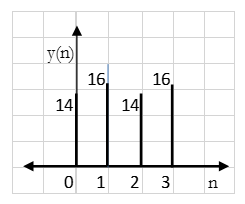
Result: y(n) = {14, 16, 14, 16}
Q3) Given x(n)= {1,2,-1,2,4,2,-1,2}, find X[k] using DITFFT algorithm
A3) Here length of FFT=8, the flow graph can be drawn as
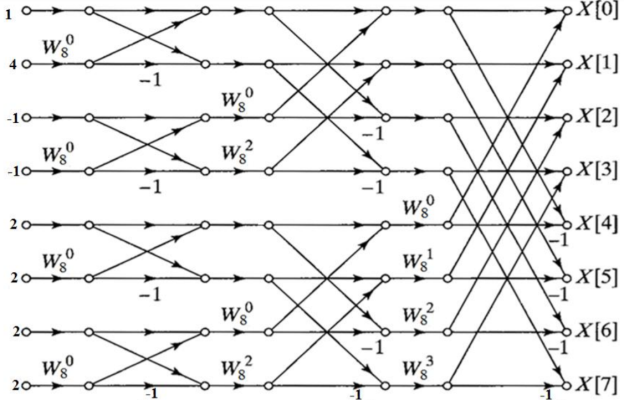
Substituting the values of twiddle factor and computing the out of each stage. For first stage value of twiddle factor is 1
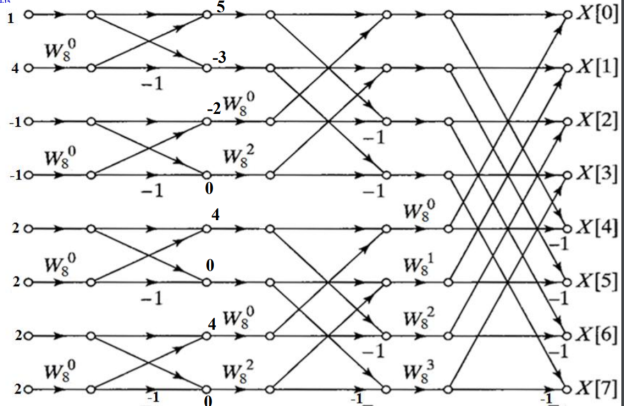
Substituting the values of twiddle factor in second stage and computing the out of second stage.
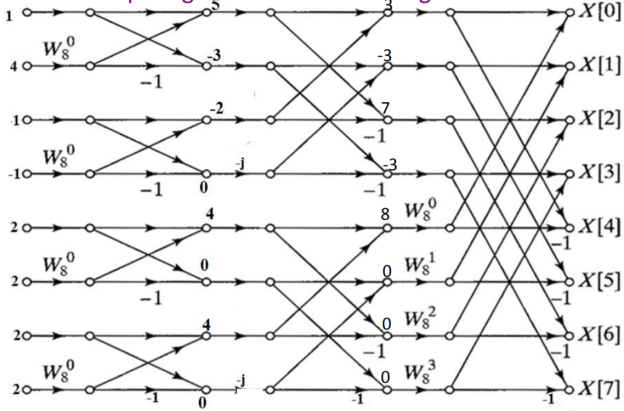
Substituting the values of twiddle factor and computing the out of third stage.

Q4) Find 8-point IDFT of a sequence X[k]={36,-4+j9.7,-4+j4,-4+j1.7,-4, -4-j1.7,-4-4j,-4-j9.7} using DIFFFT algorithm.
A4)

Second stage
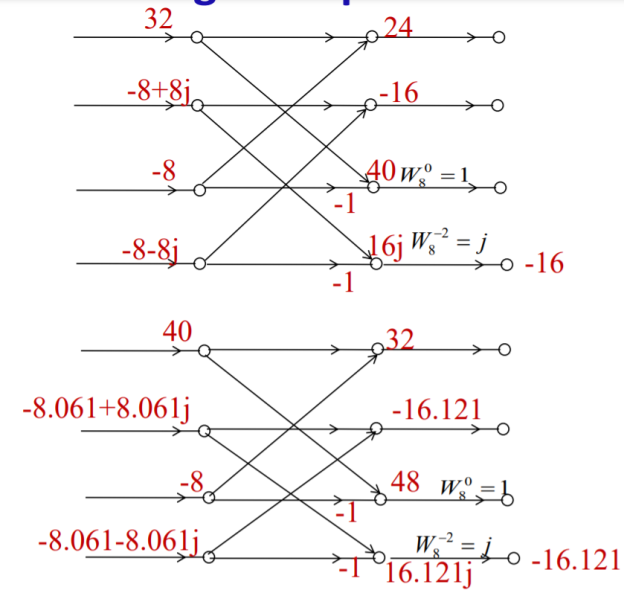

X(n) = {1,1.984,3,3.98,5,6.0151,7,8.0151}
Q5) Find the circular convolution of x(n)={1,1,1,1} and h(n)={1,0,1,0} using DIF-FFT algorithm.
A5) Let us first find 4 point DFTs of x(n) and h(n)
X[K]={4,0,0,0}
H[k]={2,2,0,0}
Y[k]= X[k].H[k]
Y[k]={8,0,0,0}
To find y(n)=x(n)⊛h(n), we shall compute IDFT of Y[k]
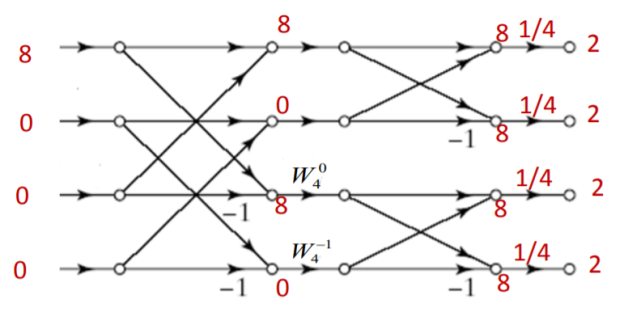
y(n)=x(n)⊛h(n)={2,2,2,2}
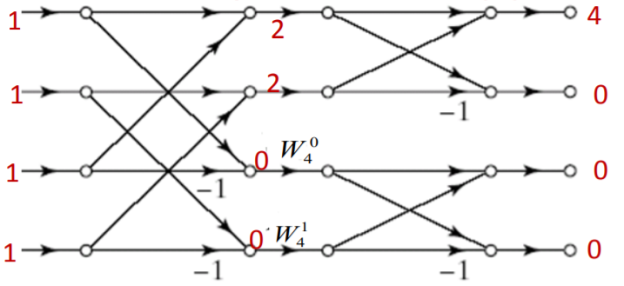
Q6) Find 8-point IDFT of a sequence X[k]={4,1-j2.414,0,1-j0.414,0, 1+j0.414,0,1+j2.414} using DIFFFT algorithm.
A6)
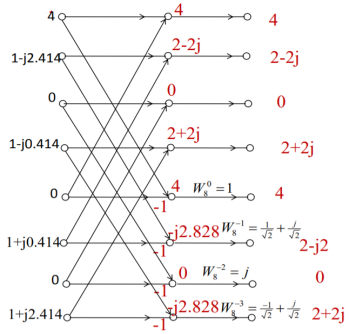
Second Stage will be
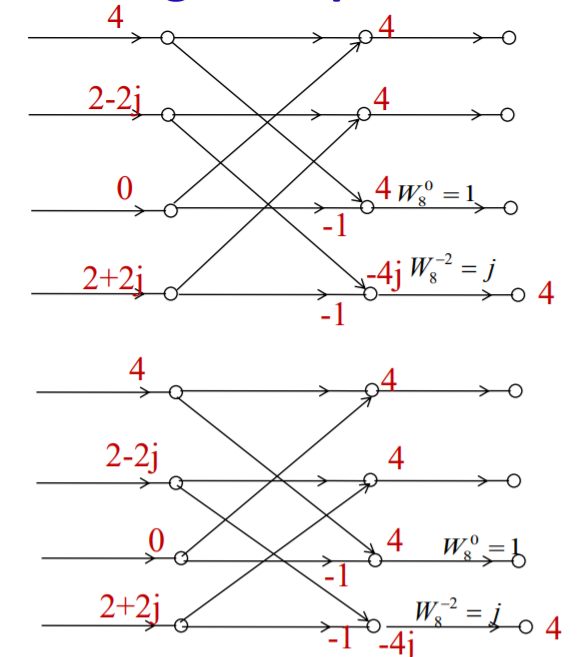
Third Stage
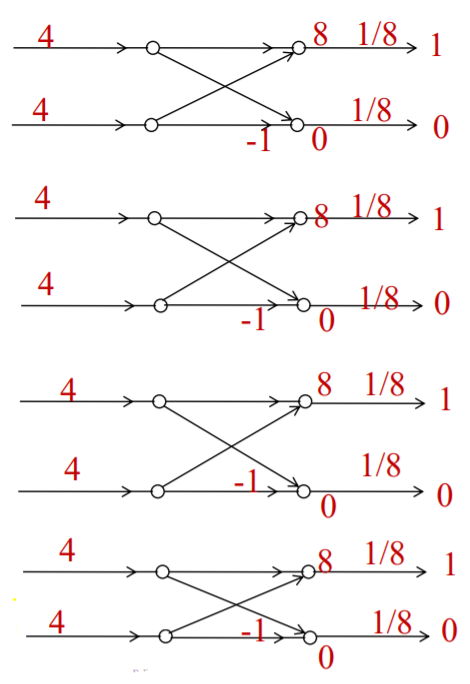
x(n)={1,1,1,1,0,0,0,0}
Q7) Consider x1 (n)={1,0.5,0.25,0.125}, x2 (n)={1,1,1,1}. Determine X1 [k] using DITFFT algorithm and X2 [k] using DIFFFT algorithm. Hence find circular convolution of x1 (n)⊛x2 (n).
A7) Let us first determine X1 [k] using DITFFT algorithm and then X2 [k] using DIFFFT algorithm. Then find IDFT of X1 [k] . X2 [k] to findx1 (n)⊛x2 (n).

X1 [k]={1.875,0.75-j0.375,0.625,0.75+j0.375}
X2 [k] using DIFFFT algorithm
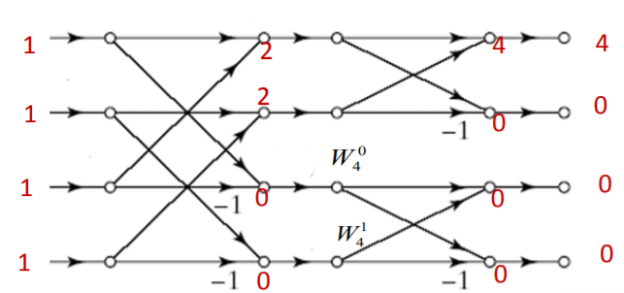
Y[k]= X1 [k].X2 [k]
Y[k]= {7.5,0,0,0}
IDFT of Y[k]
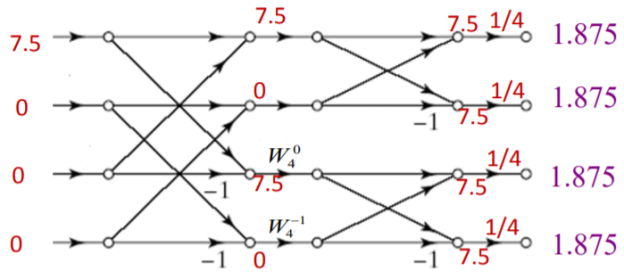
y(n)={1.875, 1.875, 1.875, 1.875}
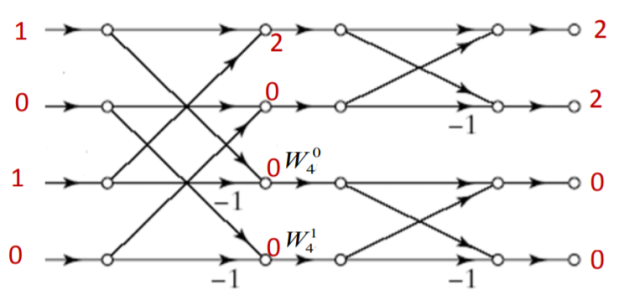
Q8) Find 8-point IDFT of a sequence X[k]={0,2+j2,-j4,2-j2,0, 2+2j,4j,2-j2} using DITFFT algorithm.
A8)
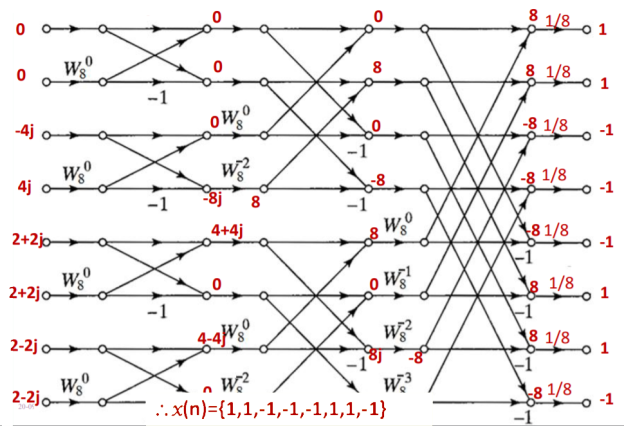
x(n)={1,1,-1,-1,-1,1,1,-1}
Q9) Compute 4-point DFT of given sequence {1,0,0,1}. Use matrix for DFT computation?
A9)
x[n] = {1,0,0,1}
N-1 = 3
N= 4
W4 = 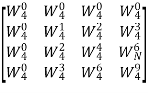 =
= 
X4 = 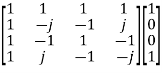
X4 = 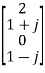
Q10) Compute the N-point DFT of x(n)=3δ(n).
A10)
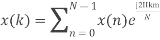
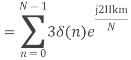


Q11) Compute the N-point DFT of x(n)=7(n−n0)
A11)
We know that,
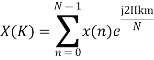
Substituting the value of x(n),
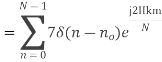
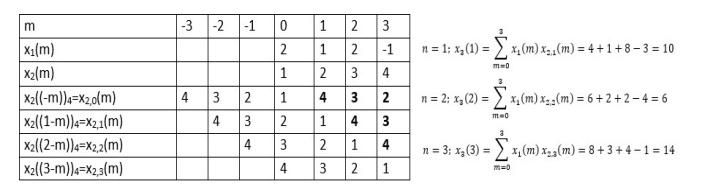
Q12) Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}
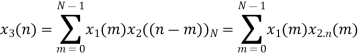
A12)
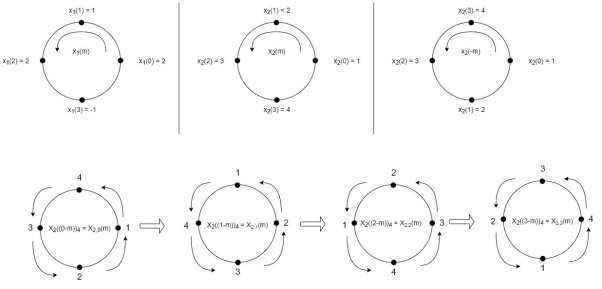
(2)
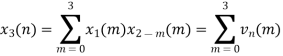
When n=0; 
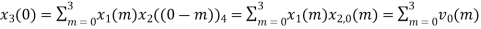
The sum of samples of v0(m) gives x3(0)
⸫ x3(0)=2+4+6-2=10
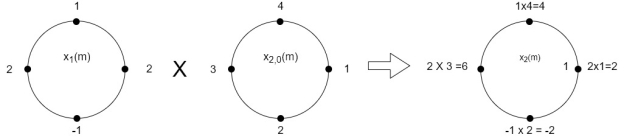
When n=1; 

The sum of samples of v1(m) gives x2(1)
⸫ x3(1)=4 + 1 +8-3=10
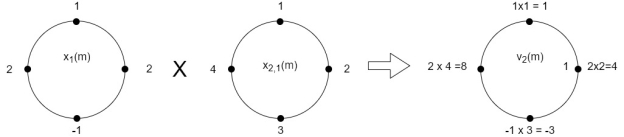
(3) When n=2; 

The sum of samples of v2(m) gives x3(2)
⸫ x3(2)=6+2+2-4=6
(4) When n=3; 


The sum of samples of v3(m) gives x3(3)
⸫ x3(3)=8+ 3+ 4-1= 14
x3(n)={10,10,6,14}

= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)
= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10
Q13) The unit sample response sequence of a system h[n] = {3,2,1}. Use the overlap save method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,-2,-1,0}. Take N=8.
A13)
- h[n] = {3,2,1}, M=3, M-1 =2
- x[n] = {2,0,-2,0,2,1,0,-2,-1,0}
- If N = L+M-1= L+3-1
8=L+2
L=6
The length of block selected is 6.
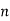 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
 |
|
| 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | … |
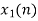 |
| 0) | 2 | 0 | -2 | 0 | 2 | 1 |
|
|
|
|
|
|
|
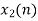 |
|
|
|
|
|
| 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 |
|
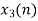 |
|
|
|
|
|
|
|
|
|
|
|
| 2 | 0 | … |
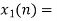 Block 1
Block 1 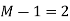 Zeros added
Zeros added
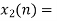 Block 2
Block 2
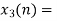 Block 3
Block 3
- Pad L-1 zeros to h[n]. Therefore, sequence will be
h[n] = {3,2,1,0,0,0,0,0}
- Perform circular convolution of h[n] with x1[n] which is shown below
| Periodic extension of data block 1 | Data block 1 | ||||||||||||||
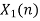 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | |
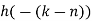 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |  |
|
|
|
|
|
| |
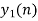 |
|
|
|
|
|
|
| 4 | 1 | 6 | 4 | -4 | 4 | 4 | 7 | |
- Take block 2 and circular convolve with h[n] as shown below
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | |
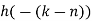 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 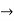 |
|
|
|
|
|
| |
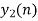 |
|
|
|
|
|
|
| 8 | 7 | 4 | -5 | -7 | 4 | 5 | 4 | |
- Add y1[n], y2[n] and so on but discard first two values from the answer and save last six values of each circular convolution as shown in figure below.
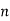 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
 | 4 | 1 | 6 | 4 | -4 | -4 | 4 | 7 |
|
|
|
|
|
|
|
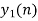 |
|
|
|
|
|
| 8 | 7 | 4 | -5 | -7 | -4 | 5 | 4 |
|
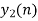 |
|
|
|
|
|
|
|
|
|
|
|
| X | X | … |
 |
|
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | -5 | -7 | -4 | 5 | 4 | … |
Final answer from overlap save method
Q14) The unit sample sequence of a system is h[n] = {3,2,1}. Use overlap add method to determine its output sequence in response to the repeating input sequence {2,0,-2,0,2,1,0,0,-2,-1,0}. Take N=8.
A14)
- h[n] = {3,2,1}, M=3, M-1 =2
- x[n] = {2,0,-2,0,2,1,0,-2,-1,0}
- If N = L+M-1= L+3-1
8=L+2
L=6
From input every time 6 elements are selected and two zeros (M-1) are padded after them as shown below.
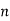 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | … |
|
 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | -2 | -1 | 0 | 2 | 0 | -2 | 0 | … | 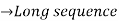 |
 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 |
|
|
|
|
|
|
|  |
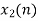 |
|
|
|
|
|
| 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 |
| 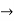 |
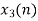 |
|
|
|
|
|
|
|
|
|
|
|
| -2 | 0 | … | 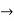 |
Breaking up long input sequence into blocks of data
- Pad L-1 zeros to h[n] sequence. Therefore, sequence will be
h[n] = {3,2,1,0,0,0,0,0}
- Perform circular convolution of h[n] with x1[n] which is shown below
| Periodic extension of data block 1 | Data block 1 |
| ||||||||||||||||
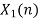 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 2 | 0 | -2 | 0 | 2 | 1 | 0 | 0 | 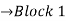 | |||
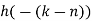 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 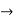 |
|
|
|
|
|
| 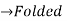 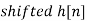 | |||
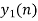 |
|
|
|
|
|
|
| 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 | 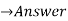 | |||
- Now circular convolution is performed for h[n] and x2[n] as shown below.
| Periodic extension of data block 2 | Data block 2 | ||||||||||||||
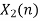 | -2 | -1 | 0 | 2 | 0 | 0 | 0 | 0 | -2 | -1 | 0 | 2 | 0 | 0 | 0 | |
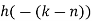 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |  |
|
|
|
|
|
| |
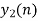 |
|
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 | |
- Do circular convolution of h[n] with different data blocks. After performing this for all we need to add up all the outputs y1[n], y2[n] and so on.
- While considering all the output sequences we do not discard any values and just keep on adding up the overlapped area as shown below.
 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
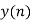 | 6 | 4 | -4 | -4 | 4 | 7 | 4 | 1 |
|
|
|
|
|
|
|
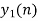 |
|
|
|
|
|
| 0 | -6 | -7 | -4 | 5 | 4 | 2 | 0 |
|
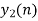 |
|
|
|
|
|
|
|
|
|
|
|
| X | X | … |
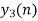 | 6 | 4 | -4 | -4 | 4 | 7 | 4 | -5 | -7 | -4 | 5 | 4 | X | X | … |
Final answer from overlap add method
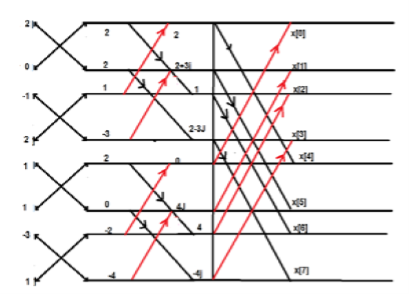
Q15) Consider the sequence x[n]={ 2,1,-1,-3,0,1,2,1}. Calculate the FFT.
A15) Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)
Since N=8 find the values W8 0 to W 87
Apply the butterfly diagram to obtain the values.
Q16) Find the DIF –FFT of the sequence x(n)= { 1,-1,-1,1,1,1,-1} using Dif-FFT algorithm.
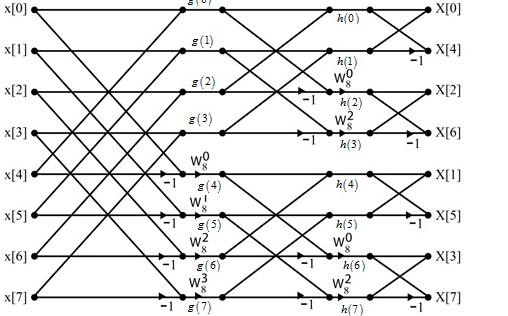
A16)
X(0)= 20 X(4) =0
X(1) = -5.828- j2.414 X(5) = -0.1716 + j 0.4141
X(2) = 0 X(6) = 0
X(3) = -0.171 – j 0.4142 X(7) = -5.8284 + j2.4142
Q17) Compare DFT and FFT?
A17)
S.NO | Fourier Transform (FT) | Discrete Fourier Transform (DFT) |
1 | FT 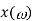 | DFT x(k) is calculated only at discrete values of . Thus DFT is discrete in nature |
2 | The range of is from –π to π or 0 to 2π | Sampling is done at N equally spaced points over version of FT. |
3 | FT is given by equation(1) | DFT is given by equation (2) |
4 | FT equations are applicable to most of infinite sequences. | DFT equations are applicable to casual, finite duration sequences. |
5 | In DSP processors and computers applications of FT are limited because x() is continuous function of . | In DSP processors and computers DFT’s are mostly used APPLICATION a) Spectrum Analysis b) Filter design |
Q18) h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n).
A18)
Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))
Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1



Q19) Find the four point DFT of the sequence x(n) = {0,1,2,3}
A19)
Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) = 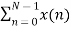 e-j2 π nk/N
e-j2 π nk/N
X(0) =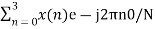
X(0) = x(0)+ x(1)+x(2) + x(3) = 0 +1+2+3 = 6
X(1) = 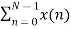 e-j2 π nk/N
e-j2 π nk/N
X(1) = 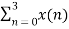 e-j2 π n/4
e-j2 π n/4
= x(0) e0 + x(1) e –j2 π /4+ + x(2) e-j4 π/4+ x(3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X(2) = 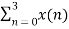 e-j2 π n2/4
e-j2 π n2/4
X(2) = 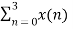 e-j π n
e-j π n
X(2) = x(0) 1+ x(1) e-j π + x(2) e-j2 π + x(3) e-j3 π
X(2) = -2
X(3) = 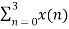 e-j2 π n3/4
e-j2 π n3/4
X(3) = x(0) e0 + x(1) e-j3 π/2 + x(2) e-j3 π + x(3) e-j9 π/2
X(3) = -2-2j.
DFT = { 6, -2+2j,-2,_2-2j}
Q20) For N =4 and
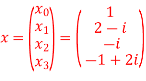
Calculate the DFT of x
A20)