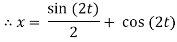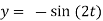Unit-1

Linear differential equations

Question-1: Solve

Sol.

Its auxiliary equation is-

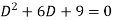
Where-

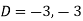
Therefore the complete solution is-

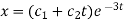
Questin-2: Solve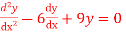

Or,

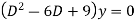
Ans. Auxiliary equation is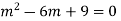

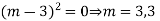
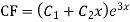
Note: If roots are in complex form i.e.

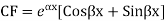
Question-3: Solve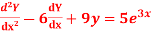

Ans. Given,

Auxiliary equation is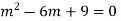

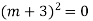
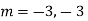
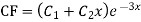
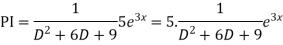
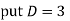
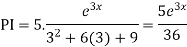
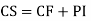
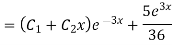
Question-4: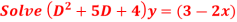

Given,

For CF,

Auxiliary equation is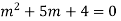

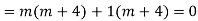
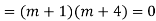
For PI

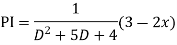
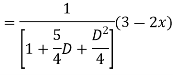
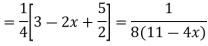
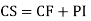
Question-5: Solve

Ans. The AE is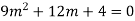

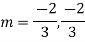
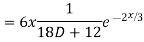
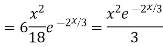
Complete solution y= CF + PI

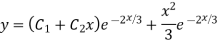
Question-6: Solve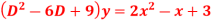

Ans. The AE is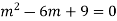

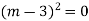
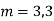
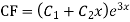
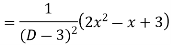
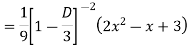
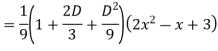
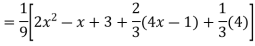
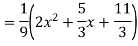
Complete solutio0n is y= CF + PI

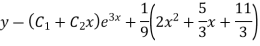
Question-7: solve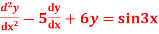

Ans. Given equation in symbolic form is

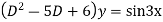
Its Auxiliary equation is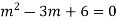

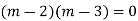
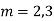
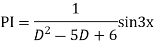
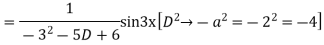
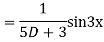
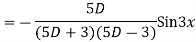
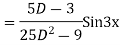
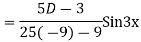
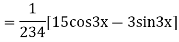
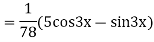
Complete solution is y= CF + PI

Question-8: Find the PI  of(D2-4D+3)y=ex cos2x

Ans.

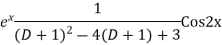
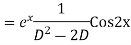
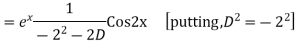
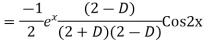
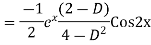
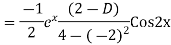
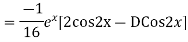
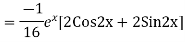
Question-9: Solve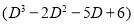

Solution:

Auxiliary equation  

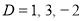
Complementary function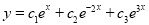

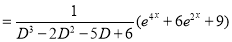
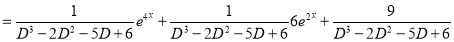
Complete Solution is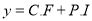  

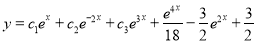
Question-10: Solve

Solution:

The auxiliary equation is     

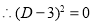
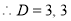
The C.F is

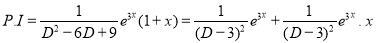
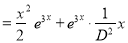
But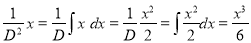

   The Complete Solution is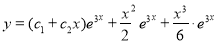

Question-11: Solve the following DE by using a variation of parameters-

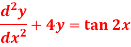
Sol. We can write the given equation in symbolic form as-

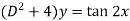
To find CF-

It’s A.E. is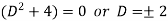

So that CF is-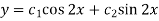     

To find PI-

Here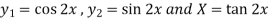

Now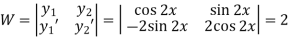

Thus PI =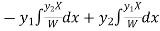 

            = 

            = 

             = 

             = 

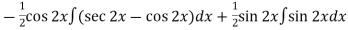
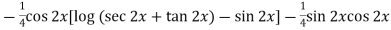
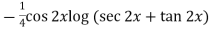
So that the complete solution is-

Question-12: Solve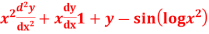

Ans. Let,

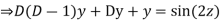
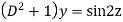
AE is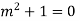

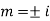
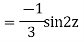
y= CF + PI

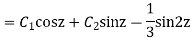
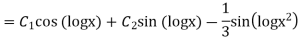
Question-13: Solve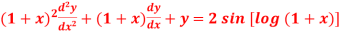

Sol. As we see that this is Legendre’s linear equation.

Now put

So that-

And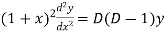

Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

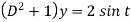
Its auxiliary equation is-

And particular integral-

               P.I. =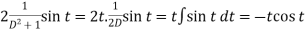

Note -

Hence the solution is -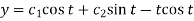

Question-14: Solve the following simultaneous differential equations-

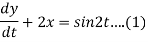
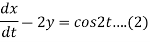
Given that x(0)=1  and y(0)= 0

Solution:

Consider the given equations,

Dy +2x = sin2t

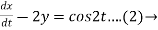Dx -2y = cos2t

By solving the above equations we get,

(D2 +4)Y =0

X(0) = 1, y(0) = 0

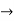A =0, B=-1