Unit 2
Q.1 Explain the parametric representation of the line connecting two end points.
A1) Fig shows a straight line connecting two end points P1 and P2. The parameter ‘u’ is set such that its values are 0 and 1 at points respectively.
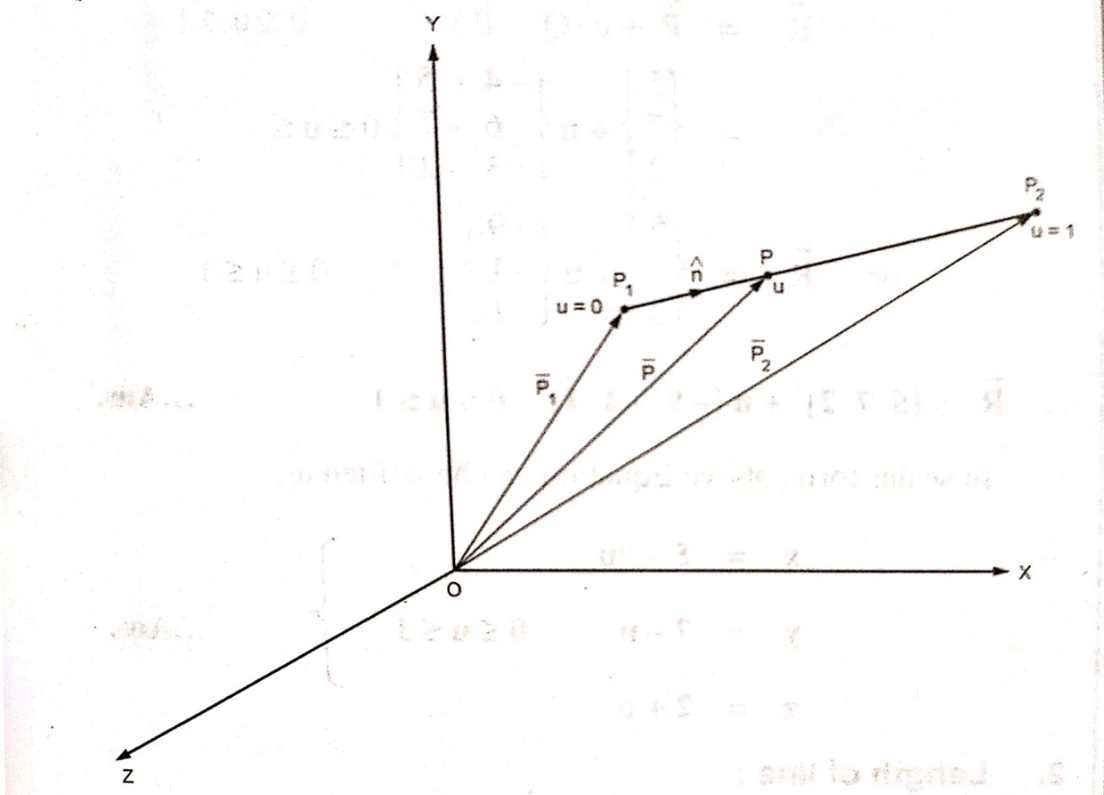
Consider any point P on the line P1P2 with general value of parameter ‘u’.
Let,
 1 be position vector for point P1
1 be position vector for point P1
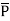 2 be position vector for point P2
2 be position vector for point P2
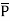 be position vector for point P
be position vector for point P
From fig
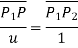
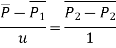
The parametric equation of line is given by
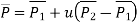
The parametric equation in scalar form is given by
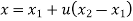
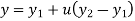
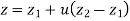
The equation of tangent vector of line P1P2 is
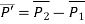
The equation of tangent vector in scalar form is
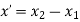
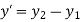

Unit vector in the direction of line is
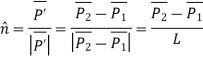
Where,
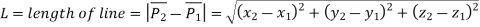
Q.2 Write a note on Hermite Cubic Spline.
A2) A cubic Hermite spline is a spline where each piece is a third-order polynomial specified in Hermite form: that is, by its values and first derivatives at the end points of the corresponding domain interval.
The cubic splines are drawn from two data points and two tangent vectors at these points.
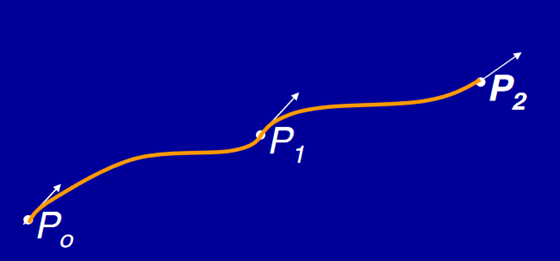
Hermite Spline
A cubic splines are cubic polynomial for their parametric representation and is given by,
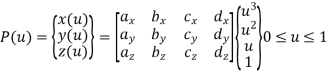
General form of parametric equation in any of X, Y or Z directions is
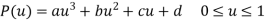
Or 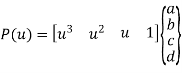
General parametric equation of hermite curve passing through two points P0 and P1 and two tangent vectors at these points P0’ and P1’ respectively is
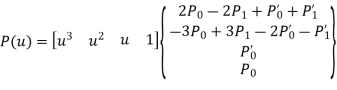
The use of Hermite Cubic Spline in CAD/CAM is not very popular due to its need of two tangent vectors.
Q.3 Explain Bezier curve with its parametric representation.
A3) “The Bezier curves uses the given data points for generating the curve and passes through first and last data points while other acts as control points.”
Bezier curves are used more than hermite cubic splines because of its flexibility to change shape of curve.

Bezier curve
Parametric equation of Bezier curve is written as,
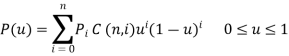
Or
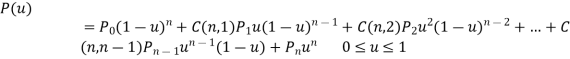
Where
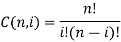
Bezier curve for n+1 data point is nth degree polynomial.
Q.4 Give the characteristics of Bezier curve
A4)
Q.5 Explain B – Spline Curve.
A5) B – Spline Curve separates the degree of polynomial of the curve from the number of data points.
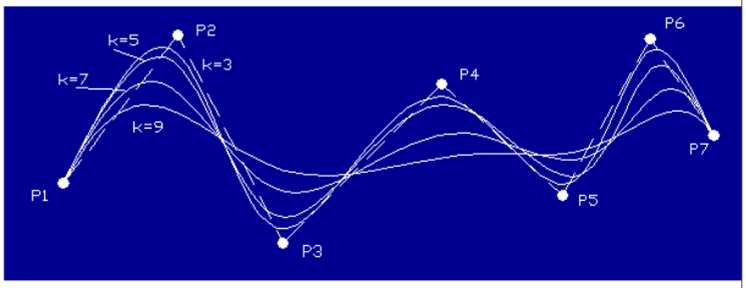
B – Spline Curve

Linear, Quadratic and Cubic B – Spline Curve
Q.6 Write a note on synthetic surfaces. Explain any two in detail.
A6) “The surface entities are defined by the set of data point are known as synthetic surfaces.”
The synthetic surfaces are needed when a surface is represented by a collection of data points. The synthetic surface are represented by the polynomial.
The various types of synthetic surfaces, used in surface modeling are:
1) Hermite bi-cubic surface
2) Bezier surface
3) B-spline surface
4) Coons surface (patch)
5) Fillet surface
6) Offset surface
Hermite Bi-Cubic surface
This 3-D surface is generated by interpolation of 4 endpoints. Bi-linear surfaces are very useful in finite element analysis. A mechanical structure is discretized into elements, which are generated by interpolating 4 node points to form a 2-D solid element.
Hermite Bi-cubic Surface
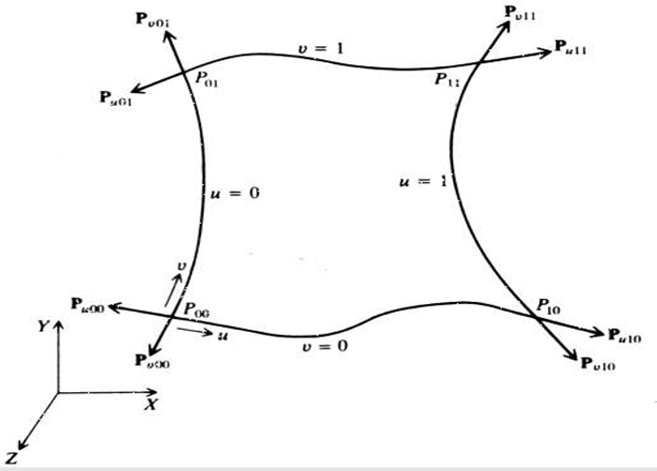
Coons surface (patch)
Coons patch or surface is generated by the interpolation of 4 edge curves as shown

Coons Surface
Q.7 Write a note on Constructive Solid Geometry
A7)
CSG Tree
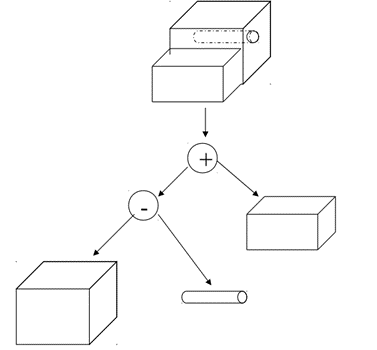
CSG Tree
Q.8 Explain different Boolean operations used in CSG.
A8) Boolean operation
– Are intuitive to user
– Are easy to use and understand
– Provide for the rapid manipulation of large amounts of data.
Because of this, many non-CSG systems also use Boolean operations.

2. Intersection
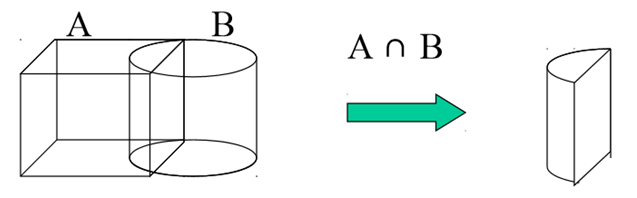
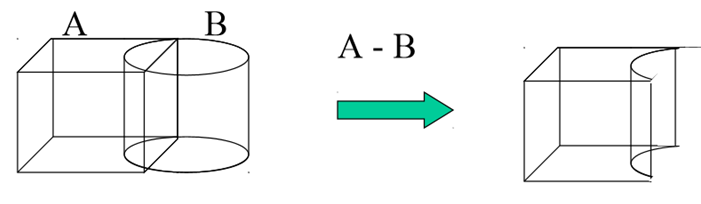
3. Difference
Q.9) Write equation of line having end points P1(3,5,8) and P2(6,4,3). Find the tangent vector and coordinates of points on line at u=0.25,0.5,0.75.
Solution:
P1(3,5,8) P2(6,4,3)
Parametric equation of ine:

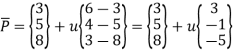

This is the equation of line.
Tangent vector of line:
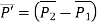
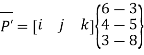

Coordinates of point:

At u = 0.25
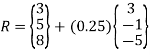

At u = 0.5
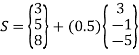
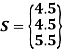
At u = 0.75
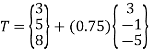
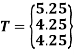
The coordinates of points at
u = 0.25 is R(3.75,4.75,6.75)
u = 0.5 is S(4.5,4.5,5.5)
u = 0.75 is T(5.25,4.25,4.25)
Q.10 A circle is represented by centre point (5,5) and radius 6 units. Find the parametric equation of circle and determine the various points on the circle in first quadrant if increment of angle is 45o and 90o.
Solution:
Pc (xc, yc, zc) = (5,5,0)
Parametric equation of circle is given by
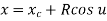
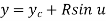
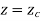
Where, 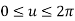
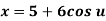

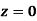
Where, 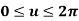
Coordinates of points on circle are given in table:
Points | u | x | y | (x,y) |
P1 | 0 | 11 | 5 | (11,5) |
P2 | 45 | 4.5 | 9.24 | (4.5,9.24) |
P3 | 90 | 5 | 11 | (5,11) |
Q.11 Calculate the points on Hermite cubic spline curve at u = 0, 0.2, 0.4, 0.6, 0.8 having end points P0 (4,4) and P1 (8,5). The tangent vector for ends P0 and P1 defined by line between P0 and P2 (5,6) and line between P1 and P3 (10,7).
Solution:
P0 (4,4) P1 (8,5) P2 (5,6) P3 (10,7)
Equation for x-coordinate:
P0x = 4 P1x = 8 P2x = 5 P3x = 10
Slope of tangent is given by
P’0x = P2x – P0x = 5 – 4 = 1
P’1x = P3x – P1x = 10 – 8 = 2
parametric equation of hermite curve for x-coordinate passing through two points P0 and P1 and two tangent vectors at these points P0’ and P1’ respectively is
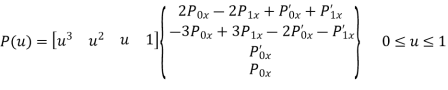
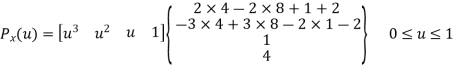
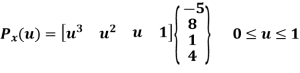
Equation for y-coordinate:
P0y = 4 P1y = 5 P2y = 6 P3y = 7
Slope of tangent is given by
P’0y = P2y – P0y = 6 – 4 = 2
P’1y = P3y – P1y = 7 – 5 = 2
General parametric equation of hermite curve passing through two points P0 and P1 and two tangent vectors at these points P0’ and P1’ respectively is
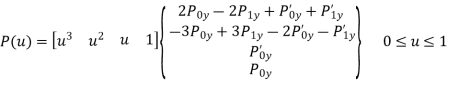
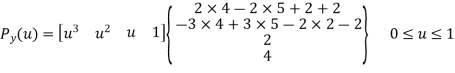
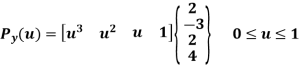
The parametric equation for hermite cubic spline is
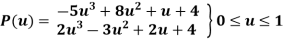
Points on the hermite cubic spline are given in table
u | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
Px(u) | 4 | 4.48 | 5.36 | 6.4 | 7.36 | 8 |
Py(u) | 4 | 4.3 | 4.45 | 4.55 | 4.7 | 5 |
(x,y) | (4,4) | (4.48,4.3) | (5.36,4.45) | (6.4,4.55) | (7.36,4.7) | (8,5) |