Unit 1
Q.1 Define Vibration. Give its causes and effects.
A1) Vibration:
“Any motion which repeats itself after an interval of time is called vibration.”
Eg: Swinging of simple pendulum
Causes of vibration:
Effect of Vibration
Produces unwanted noise, high stresses, wear, poor reliability and premature failure of one or more of the parts.
In spite of these harmful effects, it is used in musical instruments, vibrating conveyors etc.
Q.2 Explain the elements of Vibratory System
A2) Any vibratory system consists of three elements
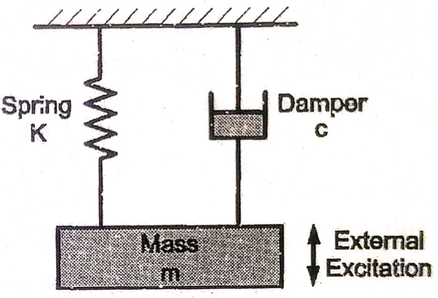
Fig. shows a basic vibratory system. The energy enters the system with the application of external force known as external excitation. Due to excitation mass is disturbed from its mean position and mass starts vibrating between two extreme positions. During this vibrations, potential energy and kinetic energy are converted into one another periodically. Hence, system continues to vibrate.
Now, if some damper is provided to oppose the motion of mass, then some amount of energy is dissipated in each cycle due to damping effect and system decays gradually.
Q.3 Give different types of Vibration
A3)
After disturbing the system, the external excitation is removed, then the system vibrates on its own. This type of vibration is known as free vibrations
eg: Simple pendulum.
3 types:-
a) Longitudinal vibrations
When the particles of the shaft or disc move parallel to the axis of the shaft, then the vibrations are known as longitudinal vibrations. In this case the shaft is elongated and shortened alternately and thus the tensile and compressive stresses are induced alternately in the shaft.
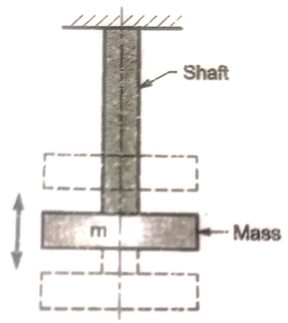
b) Transverse vibrations
When the particles of the shaft move approximately perpendicular to the axis of the shaft, then the vibrations are known as transverse vibrations. In this case the shaft is straight and bent alternately and bending stresses are induced in the shaft.
c) Torsional vibrations
When the particles of the shaft move in a circle about the axis of the shaft, then the vibrations are known as torsional vibrations.
In this case the shaft is twisted and untwisted alternately and torsional shear stresses are induced in the shaft to.
2. Forced Vibration
The vibration which is under the influences of external force is called forced vibration.
The external force applied to the body is periodic disturbing force created by unbalance.
The vibrations have the same frequency as the applied force. Due to the application of external forces the amplitude of these vibrations is maintained almost constant.
3. Damped vibration
When there is a reduction in amplitude over every cycle of vibration, the motion is said to be damped vibration.
That is if the vibrators system has a damper. The motion of the system will be opposed by it and the energy of the system will be dissipated in friction.
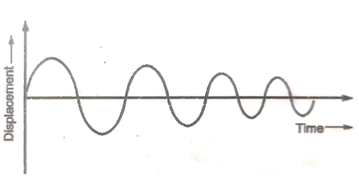
4. Undamped vibration
If there is no external resistance to the vibration of the system, then the vibration is undamped.
There is no damper. There is no loss of energy due to friction.
5. Deterministic vibration
If in the vibratory system the amount of external excitation is known in magnitude it is deterministic vibration.
6. Random vibration
If in the vibratory system the amount of external excitation is not known in magnitude it is random vibration
Non-deterministic vibrations
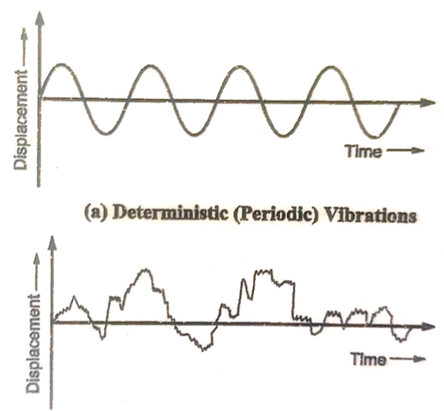
(b) random Vibration
Q.4 Explain mathematical model of a motor bike
A4) Fig (a) below shows the physical model of a motor bike with rider.
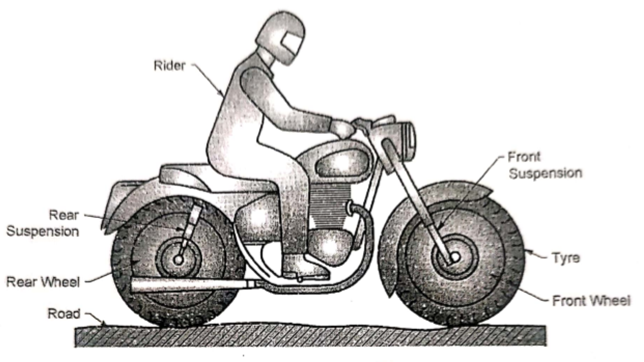
(a) Physical model of motor bike
In order to develop a mathematical model of a physical system consisting of a motor bike and a rider, following parameters are considered:
mr = mass of rider
Kr = Stiffness of rider
Cr = Damping coefficient of rider
mv = mass of motor bike (except wheels)
Ks1 = Stiffness of rear suspension
Cs1 = Damping Coefficient of rear suspension
Ks2 = Stiffness of front suspension
Cs2 = Damping Coefficient of front suspension
Mw = mass of each wheel
Kt = Stiffness of each tyre
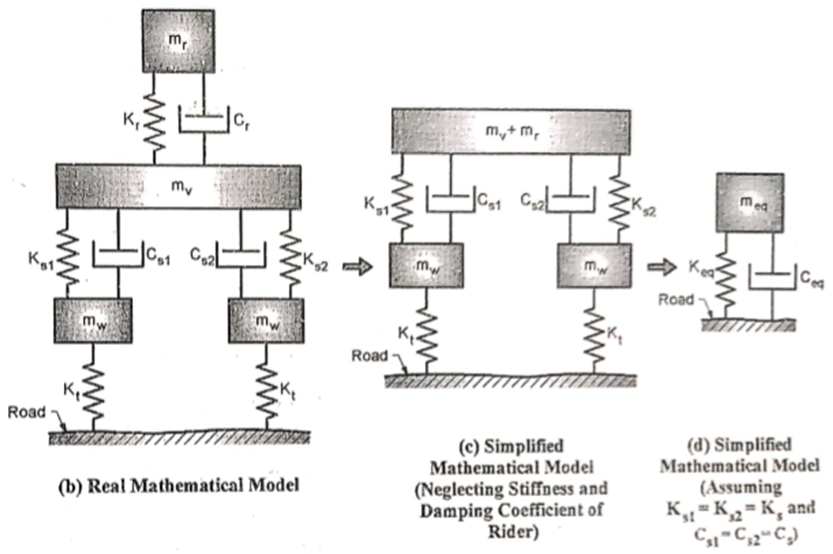
Fig (b) shows the real mathematical model of motor bike with rider.
If the stiffness and damping coefficient of rider is neglected, the mathematical model can be simplified as shown in Fig (c) and assuming the front and rear suspension are identical, the mathematical model can be simplified as shown in Fig (d)
Q.5 Formulate differential equation of motion for undamped free vibration.
A5)
A spring mass system as shown in Figure
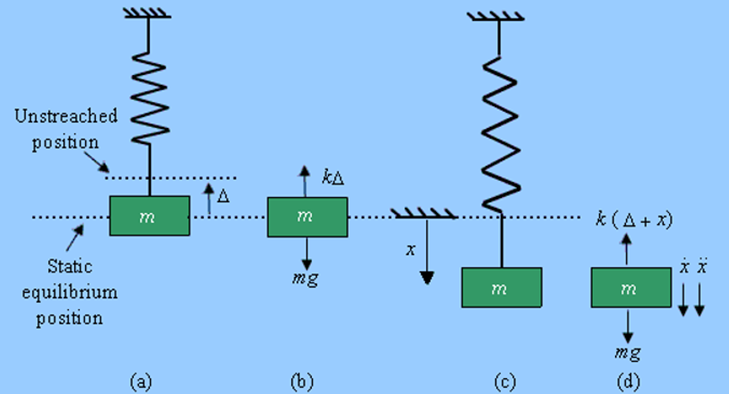
The direction of x in the downward direction is positive. Also, velocity, 
, acceleration, 
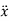, and force, F, are positive in the downward direction
According to D’Alembert’s Principle, a body or a system which is not in static equilibrium due to acceleration it possesses, can be brought to static equilibrium by introducing the inertia force on it.
From Figure (d) on application of Newton's second law, we have
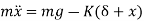
From fig (b) we have
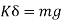
i.e. spring force due to static deflection is equal to weight of the suspended mass
So, the above equation becomes
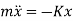
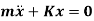
2. D’Alembert’s Method
According to D’Alembert’s Principle, a body or a system which is not in static equilibrium due to acceleration it possesses, can be brought to static equilibrium by introducing the inertia force on it.
By D’Alembert’s Principle
From fig (d)
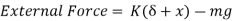
Therefore,
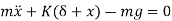
From fig (b) we have
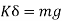
We get,
3. Energy Method
In a conservative system (i.e. with no damping) the total energy is constant, and differential equation of motion can also be established by the principle of conservation of energy.
By law of conservation of energy
Total Energy = Constant
KE + PE = Constant
The equation will be given as
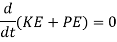
Kinetic Energy is given as
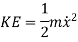
Potential energy PE is stored in the form of strain energy in elastic deformation
Therefore,
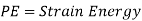
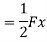
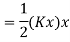
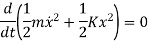
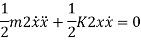
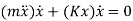
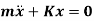
Q.6 Write a note on damping. Explain its types
A6) Damping
The external resistance which is provided to reduce the amplitude of vibrations is known as damping.
Types of damping
Based on the method of providing the resistance to the vibrations, the damping is classified into three types
When the system vibrates in a fluid medium, the resistance is offered to the vibratory body and the damping is viscous damping. The resistance is known as damping resistance or damping force.
Damping force is proportional to the relative velocity between two surfaces
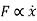
The constant of proportional ‘c’ is known as damping coefficient and is defined as damping force per unit velocity.
There are two types of viscous damping
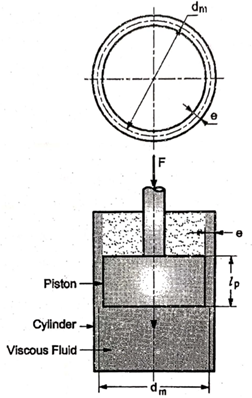
Fluid dashpot damping consists of a piston moving inside a cylinder filed with viscous fluid.
The damping coefficient ‘c’ for fluid dashpot damping can be given as
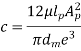
Where,
= viscosity of fluid
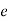= clearance between piston and cylinder
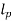= length of piston
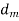= mean diameter of annular area between piston and cylinder
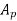= Cross-sectional area of piston
b. Eddy current damping
Eddy current damping is based on the principle of magnetic flux. It consists of a magnet and non-ferrous metal as shown in fig.
When the plate moves between north and south poles of a magnet in the direction perpendicular to the magnetic flux, current is induced in a plate and is proportional to the velocity of plate. This current is in the form of eddy current that sets up a magnetic field in the direction opposite to the original magnetic flux. Thus, there is resistance to the motion of the plate in a magnetic field which results in damping.
2. Coulomb or Dry Damping
Damping due to friction between two rubbing surfaces is called dry or coulomb damping.
3. Material or structural or solid or Hysteresis Damping
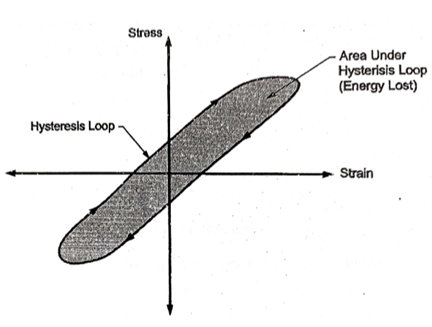
This type of damping occurs in all vibrating system due to elasticity of material. When the materials are deformed, energy is absorbed and dissipated to surrounding in the form of heat. This effect due to internal friction of molecules of material is used for damping effect and damping is material or solid damping.
When a body with material damping is subjected to vibrations, the stress-strain diagram for a vibrating body is in the form of hysteresis loop as shown in fig. Hence it is also called as hysteresis damping.
Q.7 Explain Different cases of damped system
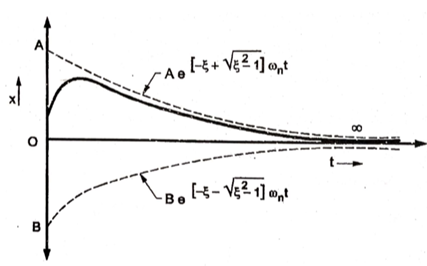
A7) Depending upon the value of damping factor or damping ratio, there are three cases of damped system
If the damping ratio ‘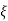
’ is greater than one or damping coefficient ‘c’ is greater than critical damping coefficient, then the system is said to be over damped.
or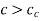 
The general solution of differential equation in over-damped system is given as,
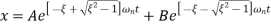
The values of constant A and B are
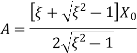
And
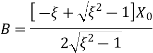
2. Critically damped system:
If the damping ratio ‘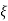
’ is equal to one or damping coefficient ‘c’ is equal to critical damping coefficient, then the system is said to be critically damped.
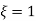or 
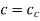
The general solution of differential equation in critically damped system is
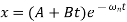
Where,
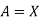0 and 
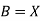0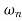
3. Under-damped system:
If the damping ratio ‘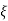
’ is less than one or damping coefficient ‘c’ is less than critical damping coefficient, then the system is said to be under damped.
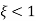or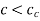 
The general solution of differential equation in under-damped system is given as
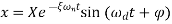
Q.8 A 200-kg machine is placed at the end of 1.8-m-Iong steel cantilever beam. The machine is observed to vibrate with a natural frequency of 21 Hz. Find the equivalent stiffness of the system.
A8)
The natural frequency of the system is
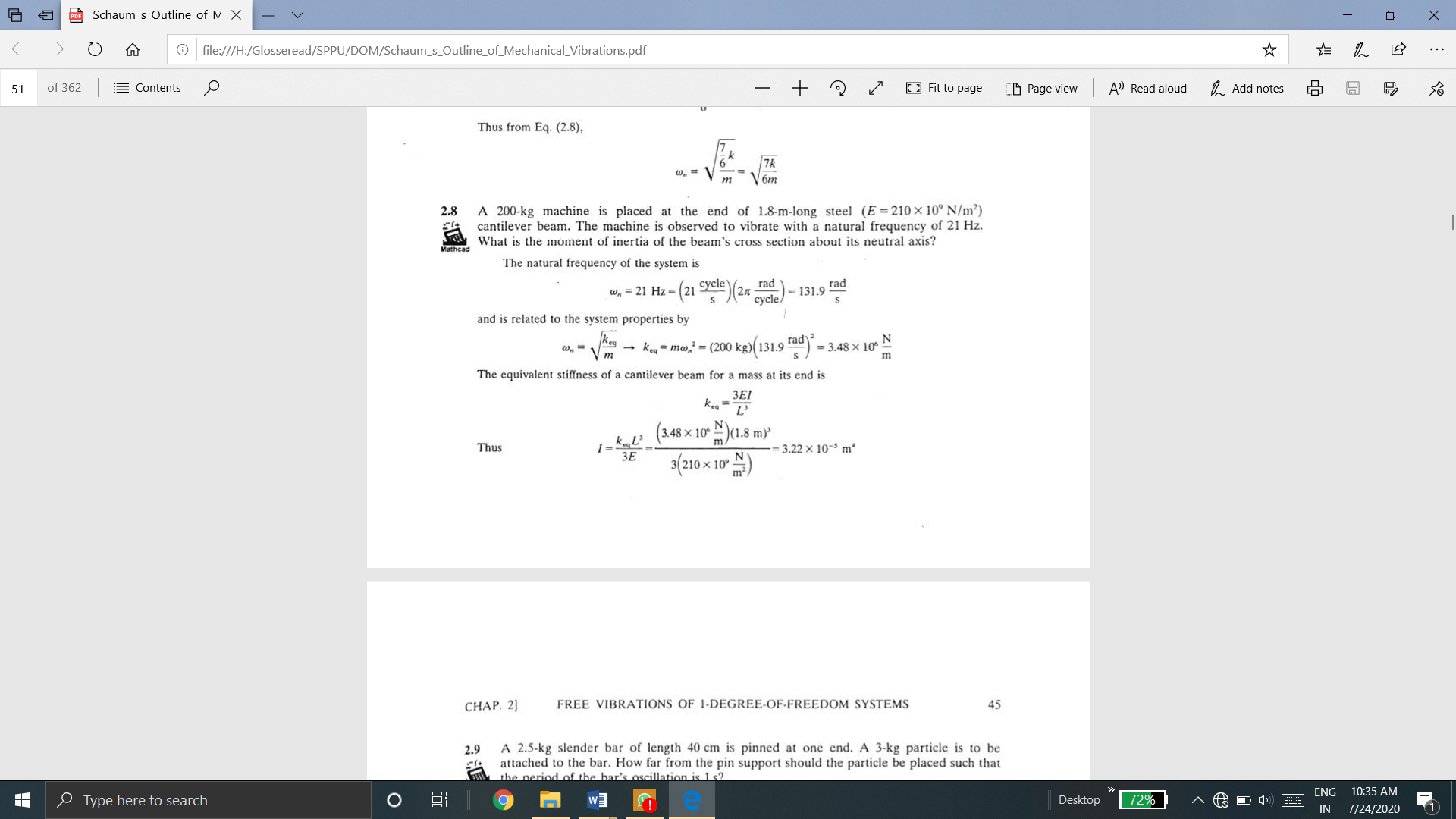
Also,
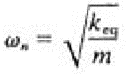
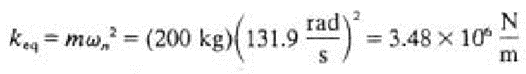
Q.9 A 500-kg vehicle is mounted on springs such that its static deflection is 1.5 mm. What is the damping coefficient of a viscous damper to be added to the system in parallel with the springs, such that the system is critically damped.
A9)
The static deflection is related to the natural frequency by
The addition of a viscous damper of damping coefficient c leads to a damping ratio of
The system is critically damped when the damping ratio is I, requiring a damping coefficient of
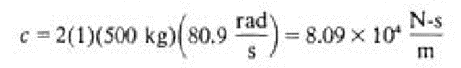
Q.10 A free vibrations test is run to determine the stiffness and damping properties of an elastic element. A 20-kg block is attached to the element. The block is displaced 1 cm and released. The displacement of the block at the end of the first cycle is 0.005 m and the damped natural period is 0.06 s. Determine k and c [or this element.
A10)
The displacement of the block at the end of the first cycle is 0.005 m. The logarithmic decrement is calculated as
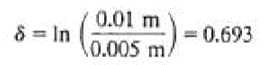
from which the damping ratio is determined
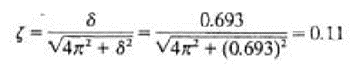
The damped natural period is determined as 0.06 s. The damped natural frequency is
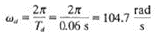
The natural frequency is calculated from
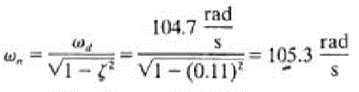
Thus the stiffness and damping coefficient are calculated
Q.11 The block in the system of Fig. is displaced 10 mm and released. How many cycles of motion will be executed?
A11)
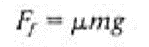
Thus the decrease in amplitude per cycle is given by
Motion will cease when the amplitude is such that the spring force cannot overcome the friction force. The resulting permanent displacement is given by
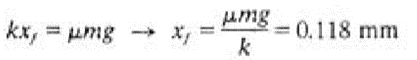
Hence the number of cycles is
Hence 22 cycles will be executed.
