Unit 3
Q.1 What is two degree of freedom system? Write governing differential equation for following system.
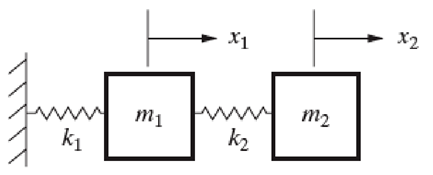
A1) Two degree of freedom system
The System which require two independent co-ordinates to specify its motion at configuration at instant is called two degree of freedom system. – Example:
There are two equations of motion for a 2DOF system, one for each mass (more precisely, for each DOF). Such equations are called coupled differential equation.
Consider a system with 2 masses and 2 springs having 2 DOF as shown in fig.
FBD of each mass is
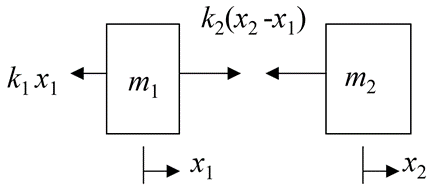
From FBD
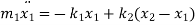

Rearranging the terms
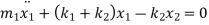
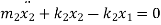
Q.2 What is 2 DOF torsional vibration system? Write the governing differential for the same.
A2) When the particles of the shaft move in a circle about the axis of the shaft, then the vibrations are known as torsional vibrations. Consider, the following torsional vibration system.
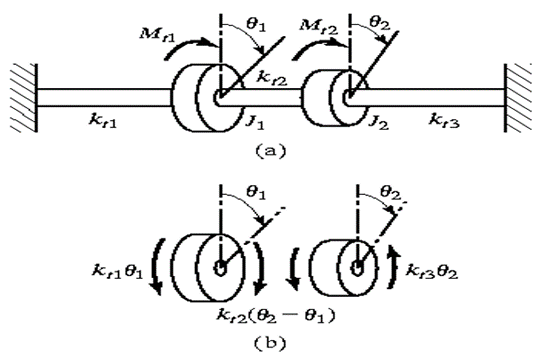
(a) Torsional system (b) FBD of disc
This system requires two FBD of two different mass discs of the same system. Hence, this system is a 2DOF torsional vibration system.
The differential equations of motion are derived from fig (b) as
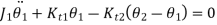

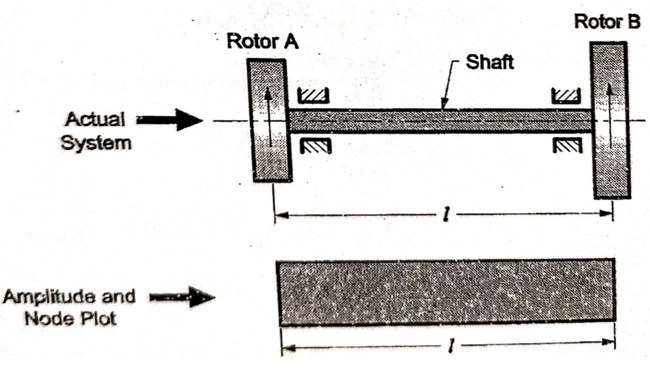
Q.3 Explain two rotor system. Derive expression of circular natural frequency and position of node in a two rotor system.
A3) A two-rotor system consists of a shaft with two rotors A and B at its end as shown in fig.
Node Point
There is a point or a section of the shaft which remains untwisted. This point or section where amplitude of vibration is zero is known as node point or nodal section.
Two rotor system with shafts AB carrying rotors A and B at ends can be considered as equivalent to two single rotor system with:
Let,
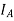 and
and 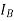 = Mass moment of Inertia of rotors A and B
= Mass moment of Inertia of rotors A and B
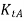 and
and 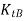 = Torsional stiffness of shaft NA and NB
= Torsional stiffness of shaft NA and NB
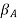 and
and 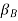 = Amplitude of vibration of rotor A and rotor B
= Amplitude of vibration of rotor A and rotor B
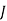 = Polar Moment of Inertia of shaft
= Polar Moment of Inertia of shaft
Circular natural frequency for single rotor system is given by
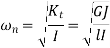
Therefore, circular natural frequency for shaft NA and rotor A
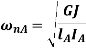
And, circular natural frequency for shaft NB and rotor B
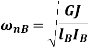
To find position of node i.e. 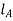
The circular frequencies of shaft are same
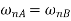
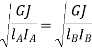
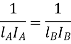
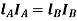
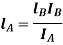
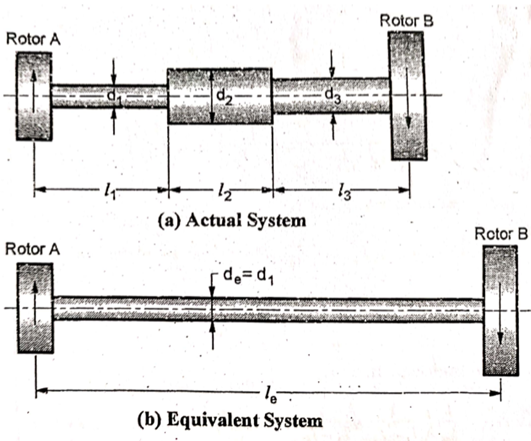
Q.4 What is torsionally equivalent system? Derive expression for equivalent length of shaft.
A4) In two rotor and three rotor system, it is assumed that the diameter of shaft is uniform. But in actual practice, the shaft may have different diameters for different lengths. If the shafts of different diameters are replaced by a theoretically equivalent shaft of a uniform diameter, as shown in fig, such shafts are called as Torsionally equivalent shaft.
Let 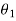 ,
,  and
and  be the angles of twist for shafts of length
be the angles of twist for shafts of length 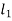 ,
, 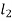 and
and 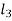 with diameters
with diameters 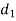 ,
, 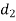 and
and 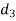 respectively.
respectively.
Let 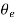 , be the angle of twist for torsionally equivalent shaft of length
, be the angle of twist for torsionally equivalent shaft of length 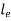 with diameter
with diameter 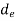 .
.
Total Angle of twist for actual shaft
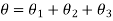
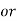
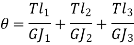
Angle of twist for equivalent shaft
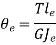
Angle of twist of equivalent shaft = Total Angle of twist for actual shaft
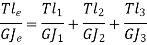
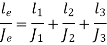
Now,

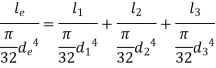
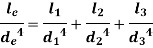
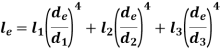
Generally, diameter of equivalent shaft is taken as one of the diameters of actual shaft. For, e.g. 
Q.5 Find the frequency equation for the system shown below.

Consider a system as shown in fig
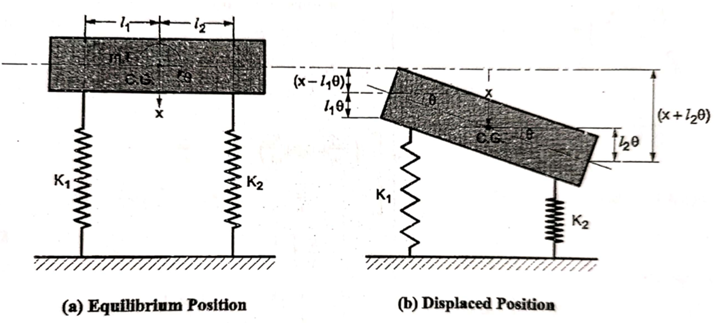
Let ‘I’ be the MI of a body with mass ‘m’ about CG
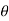 be the angular displacement at any instant and
be the angular displacement at any instant and
 be the linear displacement at that instant.
be the linear displacement at that instant.
From fig (b) compression of spring can be given as
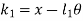
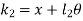
FBD of the system is shown below
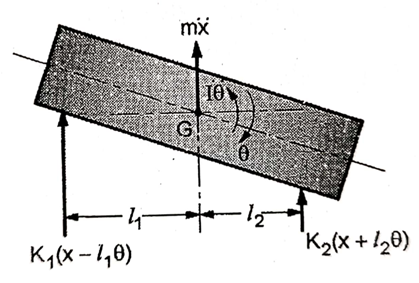
From fig., the differential equation of motion for the system are
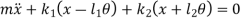
And
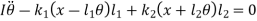
Or
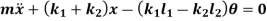
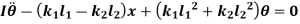
The above equations have both terms 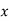 and
and 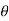 . Such equations are called as coupled equations.
. Such equations are called as coupled equations.
Solution for these two equations under steady state conditions are given by

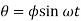
Where  and
and 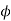 are amplitudes of vibration for linear and angular motion respectively
are amplitudes of vibration for linear and angular motion respectively
Therefore,
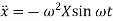
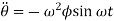
Substituting values of 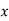 ,
, 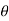 ,
, 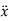 and
and  in below equation
in below equation
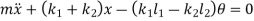
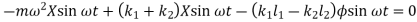
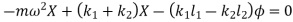
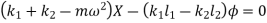
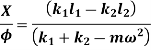
Now, substituting values of 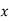 ,
, 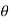 ,
, 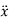 and
and  in below equation
in below equation
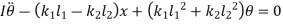
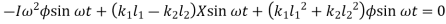
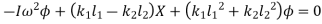
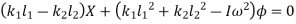
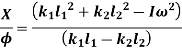
Equating both equations
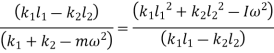
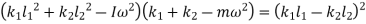
Solving above equation, we get
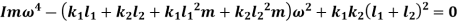
Q.6 Explain zero frequency vibration.
A6) If two rotors A and B rotate in same direction with same speed, then the shaft is said to vibrate with zero frequency. In this condition, amplitude of vibration at both ends will be in same direction. Such behavior is called as zero frequency behavior.
Q.7 Two subway cars as shown in fig. have 2000 kg mass each and concentrated by a coupler can be modeled as a spring of stiffness K = 200 kN/m. Write the equation of motion and determine the natural frequencies and mode shapes.
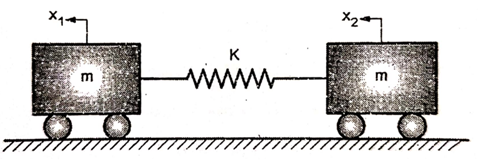
A7)
FBD of each mass is as follow
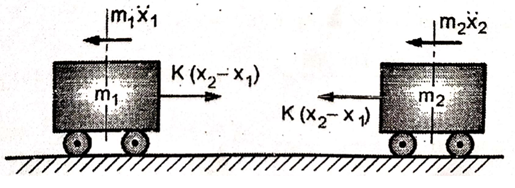
From FBD
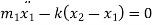
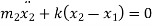
Or
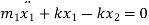
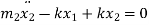
Solution for 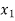 and
and 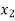 are
are


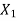 = Amplitude of vibration of mass
= Amplitude of vibration of mass 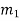
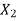 = Amplitude of vibration of mass
= Amplitude of vibration of mass 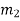
Differentiating two times, we get acceleration

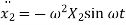
Substituting values of displacement and acceleration in equation of motion for first mass

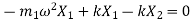
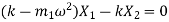
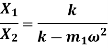
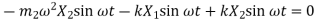
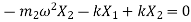
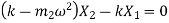
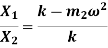
Therefore,
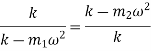

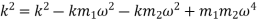
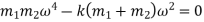
Substituting,  2000 kg and
2000 kg and 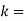 280 kN/m
280 kN/m
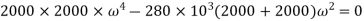
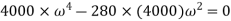
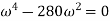
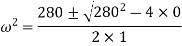

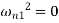 or
or 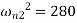
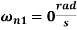 and
and 
For first mode shape,
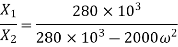
Substituting 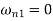
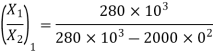

For second mode shape,

Substituting 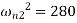
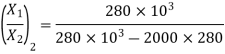
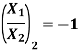
Q.8 The flywheel of an engine driving a dynamo has mass of 200 kg and has a radius of gyration of 300 mm. The shift at the end of flywheel has an effective length of 255 mm. The dynamo shaft has a diameter of 43.75 mm and had a length of 200 mm. Neglecting the inertia of the shaft and occupying calculate the frequency of the torsional vibrations and position of node. Take the modulus of rigidity for shaft material at 80 GPa.
A8) Mass movement of inertia for rotor A,
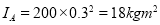
Mass movement of inertia for rotor B,
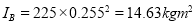
Modulus of rigidity for shaft material,

1. Equivalent length
The equivalent length of shaft having diameter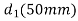 is,
is,

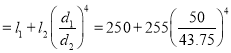

2. Position Node:
We know that,
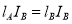
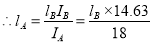
Or, 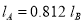
But,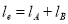
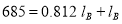
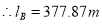
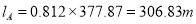
3. Natural Frequency: The natural circular frequency of two rotor system is,
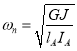 or
or 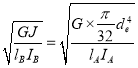
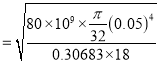
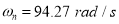
The natural frequency of two rotor system is,
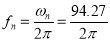 or
or 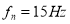
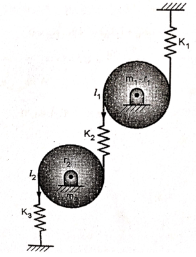
Q.9 Find the natural frequencies of the system shown in fig.
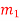 = 10 kg
= 10 kg 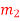 = 12 kg
= 12 kg 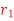 = 0.1 m
= 0.1 m 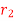 = 0.11 m
= 0.11 m
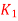 = 40 x 103 N/m
= 40 x 103 N/m  = 50 x 103 N/m
= 50 x 103 N/m  = 60 x 103 N/m
= 60 x 103 N/m
A9)
1. Frequency Equation:
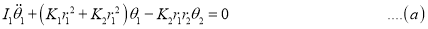
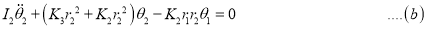
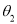
Assume,

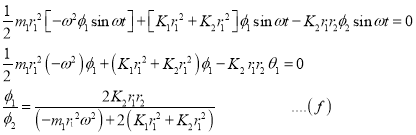
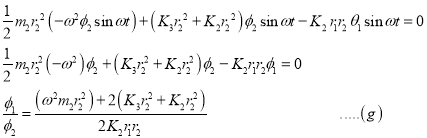
From equation (f) and (g),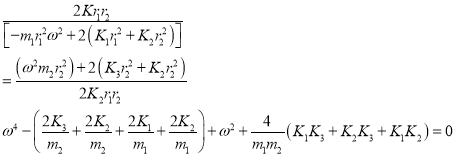
2. Two natural frequencies:
Substituting the values 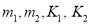 and
and 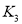
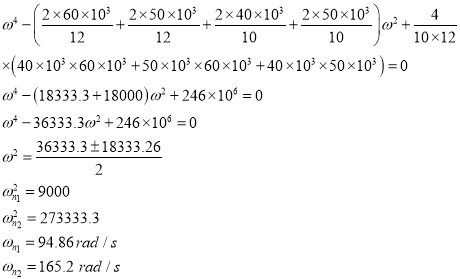
Q.10 Find the natural frequencies and mode shapes for the torsional system shown in fig. Assume 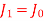 ,
, 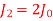 and stiffness of each shaft as
and stiffness of each shaft as 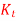
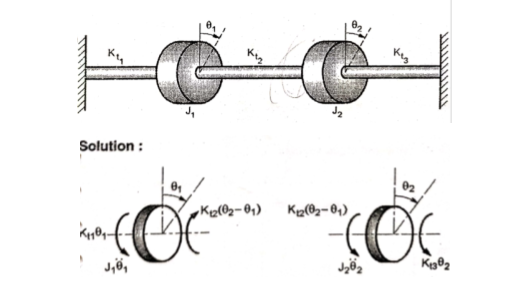
1. Frequency Equation:
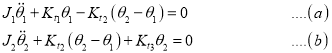
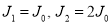
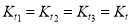
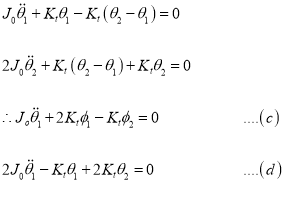

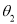

Therefore,
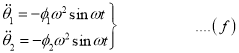
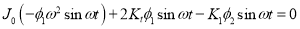
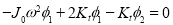
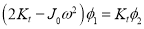

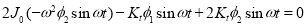


From equations (g) and (b)

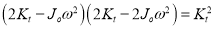
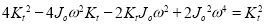
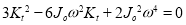
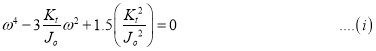
2. Two natural frequencies:

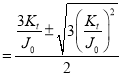
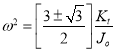
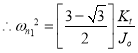 and
and 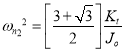
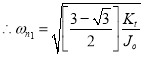 and
and 