undefined | unit 2 ideal gas and second law of thermodynamics

THERMO

UNIT 2

Ideal Gas and Second law of Thermodynamics

Q1) Explain and derive the characteristic equation of state.

A1) An imaginary gas which obeys this law p v = R*T = constant, at all Pressure and Temperature is called an ideal gas, and the equation is called Characteristic equation of state for ideal gas.

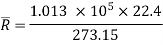
= 8314.3 Nm/kg mol K

This R* is called universal gas constant.

Also, specific volume, v = V / n,

V = total volume and n = number of moles.

∴ p V = n R*T

But, n = m/M, where M – is Molecular weight

∴ p V = m R*T / M

∴ p V = m R T

Where, R*/ M = R = Characteristic gas constant

The Value of “R” will depend upon particular gas and can be found

using R* = 8314.3 J/mol K and M – molecular weight of gas.

Q2) Give all the ideal gas laws.

A2)

Boyle's law: (at T = const)

P ∝ 1/ V or PV = k

2. Charles' law :(at P = const)

V ∝ T or V/T = k

3. Gay - lussac's law :(at V = const)

P ∝ T or P/T = k

4. Avogadro's law : Avogadro's law states that, "equal volumes of all gases, at the same temperature and pressure, have the same number of molecules”

V ∝ n or V/n = k

Where, n is the amount of substance of the gas (measured in moles).

Q3) Explain the second law of thermodynamics.

A3) Second Law of Thermodynamics:

STATEMENTS OF SECOND LAW OF THERMODYNAMICS:

The second law of thermodynamics has two statements put forward by two scientists.

Clausius statement: “It is impossible for a self-acting machine working in a cyclic process unaided by any external agency, to convey heat from a body at a lower temperature to a body at a higher temperature”. In other words, heat cannot flow from a colder to a hotter body.

Kelvin Planck statement: “It is impossible to construct an engine, which while operating in a cycle produces no other effect except to extract heat from a single reservoir and do equivalent amount of work”.

Although the Clausius and Kelvin-Planck statements appear to be different, they are really equivalent in the sense that a violation of either statement implies violation of other.

Q4) State the Equivalence of Clausius Statement to the Kelvin-Planck Statement.

A4) Equivalence of Clausius Statement to the Kelvin-Planck Statement

Consider a higher temperature reservoir T1 and low temperature reservoir T2. Fig. shows a heat pump which requires no work and transfers an amount of Q2 from a low temperature to a higher temperature reservoir (which is a violation of the Clausius statement).

Let an amount of heat Q1 (greater than Q2) be transferred from high temperature reservoir to heat engine which develops a net work, W = Q1 – Q2 and rejects Q2 to the low temperature reservoir. Since there is no heat interaction with the low temperature, it can be eliminated. The combined system of the heat engine and heat pump acts then like a heat engine exchanging heat with a single reservoir, which is the violation of the Kelvin-Planck statement.

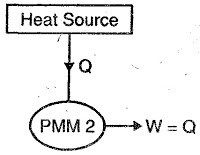
Q5) Explain the PMM2.

A5) Perpetual motion machine of second kind (PMM2)

This machine violates the second law of thermodynamics because such machines will absorb heat energy continuously from a thermal reservoir and will convert the absorbed heat energy completely in to equivalent amount of work.

This machine will have efficiency 100%, or we can say that perpetual motion machines of second kind will have higher efficiency than ideal Carnot cycle and it is not possible.

Therefore, we can say that perpetual motion machine of second kind will also does not exist as such machines violate the second law of thermodynamics.

Figure showing below a graphical representation of PMM2

Q6) Explain in detail the Carnot cycle.

A6) THE CARNOT VAPOR CYCLE

The Carnot cycle is the most efficient cycle operating between two specified temperature limits. Thus, it is natural to look at the Carnot cycle first as a prospective ideal cycle for vapor power plants.

However, the Carnot cycle is not a suitable model for power cycles.

Process 4-1 : 1 kg of boiling water at temperature T1 is heated to form wet steam of dryness fraction x1. Thus heat is absorbed at constant temperature T1 and pressure p1 during this operation.

Process 1-2 : steam is expanded isentropically to temperature T2 and pressure p2. The point ‘2’ represents the condition of steam after expansion.

Process 2-3 : heat is rejected at constant pressure p2 and temperature T2. As the steam is exhausted it becomes wetter and cooled from 2 to 3.

Process 3-4 : the wet steam at ‘3’ is compressed isentropically till the steam regains its original state of temperature T1 and pressure p1.

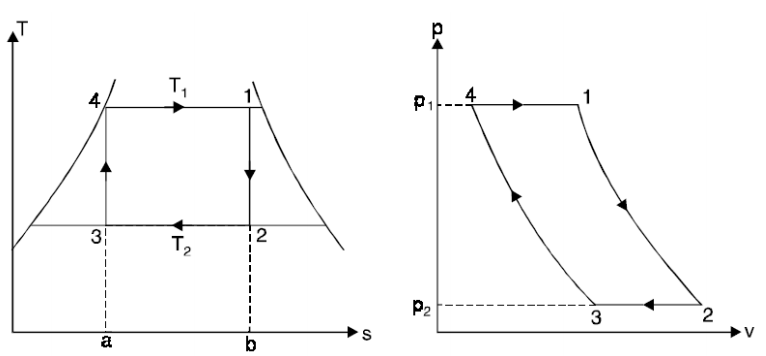
Thus cycle is completed.

Net work done = Heat supplied – heat rejected

= T1 (s2 - s3) - T2 (s2 - s3)

= (T1 – T2) (s2 - s3)

Carnot Efficiency η = Work done / Heat supplied = (T1 – T2) (s2 - s3) / T1 (s2 - s3)

= (T1 – T2) / T1

Q7) What are the limitations of Carnot cycle?

A7) Limitations or Impracticalities of Carnot Cycle:

Though Carnot cycle is simple (thermodynamically) and has the highest thermal efficiency for given values of T1 and T2, yet it is extremely difficult to operate in practice because of the following reasons:

It is difficult to compress a wet vapourisentropically to the saturated state as required by the process 3-4.

It is difficult to control the quality of the condensate coming out of the condenser so that the state ‘3’ is exactly obtained.

The efficiency of the Carnot cycle is greatly affected by the temperature T1 at which heat is transferred to the working fluid. Since the critical temperature for steam is only 374°C, therefore, if the cycle is to be operated in the wet region, the maximum possible temperature is severely limited.

The cycle is still more difficult to operate in practice with superheated steam due to the necessity of supplying the superheat at constant temperature instead of constant pressure.

Some of these problems could be eliminated by executing the Carnot cycle in a different way, as shown in Fig. B.

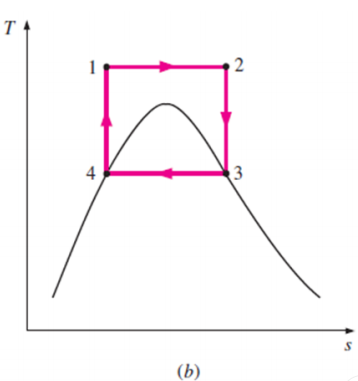
This cycle, however, presents other problems such as isentropic compression to extremely high pressures and isothermal heat transfer at variable pressures.

Thus, we conclude that the Carnot cycle cannot be approximated in actual devices and is not a realistic model for vapor power cycles.

Q8) An automobile engine consumes fuel at a rate of 28 L/h and delivers 60 kW of power to the wheels. If the fuel has a heating value of 44,000 kJ/kg and a density of 0.8 g/cm3, determine the efficiency of this engine.

A8) The power output and fuel consumption rate of a car engine are given. The thermal efficiency of the engine is to be determined.

Assumptions The car operates steadily.

Properties The heating value of the fuel is given to be 44,000 kJ/kg.

Analysis The mass consumption rate of the fuel is

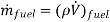= (0.8 kg/L)(28 L/h) = 22.4kg/h

The rate of heat supply to the car is

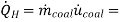(22.4kg/h)(44.000kJ/kg)=985.600 kJ/h = 273.78 kW

Then the thermal efficiency of the car becomes

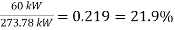
Q9) A household refrigerator with a COP of 1.2 removes heat from the refrigerated space at a rate of 60 kJ/min. Determine

(a) the electric power consumed by the refrigerator and

(b) the rate of heat transfer to the kitchen air.

A9) The COP and the refrigeration rate of a refrigerator are given.

The power consumption and the rate of heat rejection are to be determined.

(a) Using the definition of the coefficient of performance, the power input to the refrigerator is

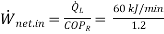= 50 kJ/min = 0.83 kW

(b) The heat transfer rate to the kitchen air is determined from the energy balance,

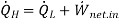= 60 +50 = 110 kJ/ min

Q10) A heat pump is used to heat a house and maintain it at 24°C. On a winter day when the outdoor air temperature is -5°C, the house is estimated to lose heat at a rate of 80,000 kJ/h.

Determine the minimum power required to operate this heat pump.

A10) Heat pump maintains a house at a specified temperature. The rate of heat loss of the house is given.

The minimum power input required is to be determined.

The power input to a heat pump will be a minimum when the heat pump operates in a reversible manner.

The COP of a reversible heat pump depends on the temperature limits in the cycle only, and is determined from,

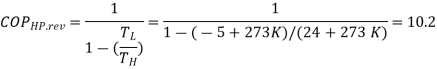
The required power input to this reversible heat pump is determined from the definition of the coefficient of performance to be

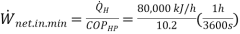= 2.18kW

Sign Up