UNIT 3
Entropy
Q1) Define Entropy.
A1) Entropy
Clausius realized in 1865 that he had discovered a new thermodynamic property and he chose to name this property entropy. It is designated S and is defined as , dS = (dQ / T)
The entropy change of a system during a process can be determined by integrating above Eq. between the initial and the final states
 (kJ/K)
(kJ/K)
Therefore, the entropy of a substance can be assigned a zero value at some arbitrarily selected reference state, and the entropy values at other states can be determined from above Eq.
Q2) Why entropy is considered as a property of the system?
A2) Entropy—a Property of a System
∮ dQ / T = 0
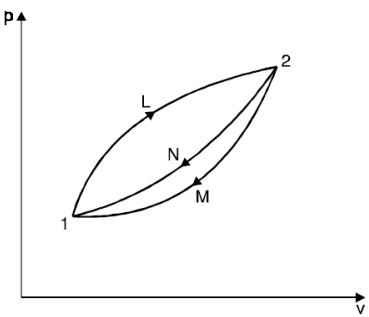
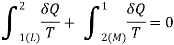
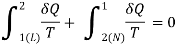
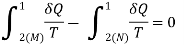
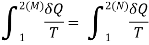
Q3) State the increase of entropy principle.
A3) THE INCREASE OF ENTROPY PRINCIPLE
reversible, as shown in Figure.
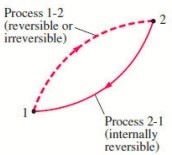
∮ dQ / T ≤ 0
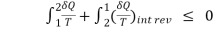
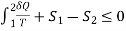
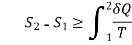
DS ≥ dQ / T
where the equality holds for an internally reversible process and the inequality for an irreversible process.
We may conclude from these equations that the entropy change of a closed system during an irreversible process is greater than the integral of ∂Q/T evaluated for that process.
The inequality sign in the preceding relations is a constant reminder that the entropy change of a closed system during an irreversible process is always greater than the entropy transfer.
That is, some entropy is generated or created during an irreversible process, and this generation is due entirely to the presence of irreversibilities.
The entropy generated during a process is called entropy generation and is
denoted by Sgen.
Noting that the difference between the entropy change of a closed system and the entropy transfer is equal to entropy generation, hence previous Eq. can be rewritten as an equality as
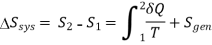
Its value depends on the process, and thus it is not a property of the system. Also, in the absence of any entropy transfer, the entropy change of a system is equal to the entropy generation.
For an isolated system (or simply an adiabatic closed system), the heat transfer is zero
ΔSisolated ≥ 0
This equation can be expressed as the entropy of an isolated system during a process always increases or, in the limiting case of a reversible process, remains constant. In other words, it never decreases. This is known as the increase of entropy principle.
Note that in the absence of any heat transfer, entropy change is due to irreversibilities only, and their effect is always to increase entropy.
The increase of entropy principle can be summarized as
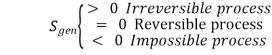
Q4) Explain the Clausius inequality principle.
A4) CLAUSIUS INEQUALITY:
The integral of dQ / T is always less than or equal to zero.
∮ dQ / T ≤ 0
This inequality is valid for all cycles in this universe without any exceptions.
To demonstrate the validity of the Clausius inequality, consider a system connected to a thermal energy reservoir at a constant thermodynamic (i.e., absolute) temperature of TR through a reversible cyclic device.
The cyclic device receives heat ∂QR from the reservoir and supplies heat ∂Q to the system whose temperature at that part of the boundary is T (a variable) while producing work ∂Wrev.
The system produces work ∂Wsys as a result of this heat transfer.
Balancing the combined system identified by dashed lines yield
ΔWc = δQR - dEc
Considering that the cyclic device is a reversible one, we have
δQR / TR = δQ / T
Eliminating ∂QR from the two relations above yields
ΔWc = TR δQ / T - dEc
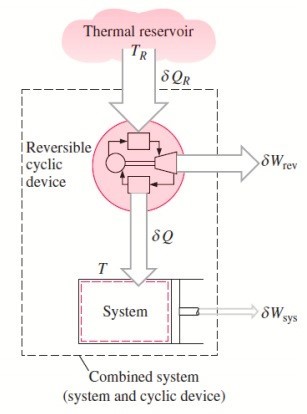
We let the system undergo a cycle while the cyclic device undergoes an integral number of cycles. Then the preceding relation becomes
Wc = TR ∮ dQ / T
Here WC is the cyclic integral of ∂WC, and it represents the net work for the combined cycle.
It appears that the combined system is exchanging heat with a single thermal energy reservoir while involving (producing or consuming) work Wc during a cycle. On the basis of the Kelvin-Planck statement of the second law, which states that no system can produce a net amount of work while operating in a cycle and exchanging heat with a single thermal energy reservoir, we reason that Wc cannot be a work output, and thus, it cannot be a positive quantity.
∮ dQ / T ≤ 0
Q5) Derive the availability function for steady flow processes.
A5) Availability Function for Steady Flow process:
The maximum work that can be done in a SF process while the control volume exchanges heat with the atmosphere at T0, is given by:
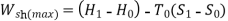
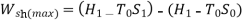
It can also be expressed as
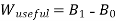
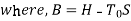
which is called the Darrieus Function.
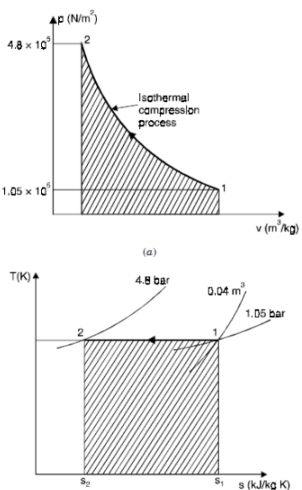
Q6) 0.04 m3 of nitrogen contained in a cylinder behind a piston is initially at 1.05 bar and 15°C. The gas is compressed isothermally and reversibly until the pressure is 4.8 bar.
Calculate :
(i) The change of entropy,
(ii) The heat flow, and
(iii) The work done.
Sketch the process on a p-v and T-s diagram. Assume nitrogen to act as a perfect gas. Molecular weight of nitrogen = 28.
A6) For Nitrogen, Initial pressure, p1 = 1.05 bar
= 1.05 × 105 N/m2
Initial volume, V1 = 0.04 m3
Temperature, T1 = 15 + 273 = 288 K
Final pressure, p2 = 4.8 bar = 4.8 × 105 N/m2
Final temperature, T2 = T1 = 288 K.
Now, using characteristic gas equation (to find mass ‘m’ of nitrogen), we have :
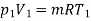
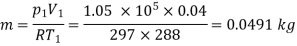
(i) The change of entropy,
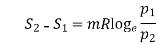
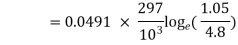
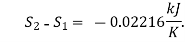
 Decrease in entropy, S1 – S2 = 0.02216 kJ/K
Decrease in entropy, S1 – S2 = 0.02216 kJ/K
 Heat rejected = Shaded area on Fig 5.32 (b)
Heat rejected = Shaded area on Fig 5.32 (b)
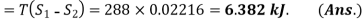
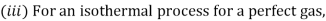
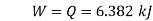
Hence, the work done on air = 6.382 kJ. (Ans.)
Q7) Air at 20°C and 1.05 bar occupies 0.025 m3. The air is heated at constant volume until the pressure is 4.5 bar, and then cooled at constant pressure back to original temperature.
Calculate:
(i) The net heat flow from the air.
(ii) The net entropy change.
Sketch the process on T-S diagram.
A7) For air :
Temperature, T1 = 20 + 273 = 293 K
Volume, V1 = V2 = 0.025 m3
Pressure, p1 = 1.05 bar = 1.05 × 105 N/m2
Pressure, p2 = 4.5 bar = 4.5 × 105 N/m2
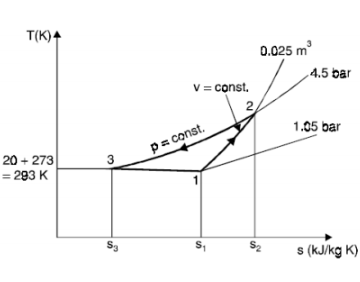
For a perfect gas (corresponding to point 1 of air),
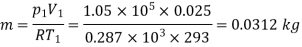
For a perfect gas at constant volume,
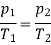
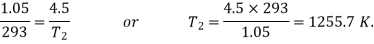
At constant volume,
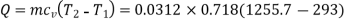
Q1-2 = 21.56 kJ.
Also, at constant pressure,
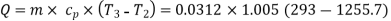
Q2 – 3 = - 30.18 kJ
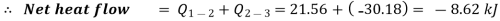
Net decrease in entropy,
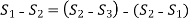
At constant pressure, 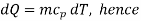
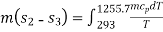
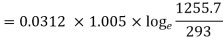
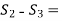 0.0456 kJ/K
0.0456 kJ/K
At constant volume, 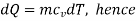
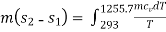
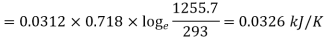
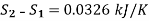
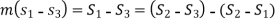
= 0.0456 – 0.0326 = 0.013 kJ/K
Q8) 0.04 kg of carbon dioxide (molecular weight = 44) is compressed from 1 bar, 20°C, until the pressure is 9 bar, and the volume is then 0.003 m3. Calculate the change of entropy.
Take Cp for carbon dioxide as 0.88 kJ/kg K, and assume carbon dioxide to be a perfect gas.
A8) For carbon dioxide:
Mass of carbon dioxide, m = 0.04 kg
Molecular weight, M = 44
Initial pressure, p1 = 1 bar = 1 × 105 N/m2
Initial temperature, T1 = 20 + 273 = 293 K
Final pressure, p2 = 9 bar
Final volume, V2 = 0.003 m3
Cp for carbon dioxide = 0.88 kJ/kg K
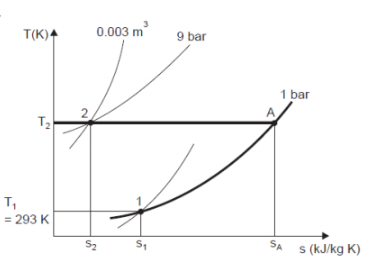
Characteristic gas constant,
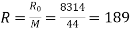 Nm/kg K
Nm/kg K
To find T2, using the relation,
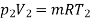

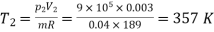
Now 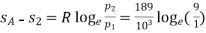
= 0.4153 kJ/kg K
Also at constant pressure from 1 to A
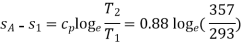
= 0.1738 kJ/kg K
Then 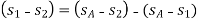
= 0.4153 – 0.1738 = 0.2415 kJ/kg K
Hence for 0.04 kg of carbon dioxide decrease in entropy,
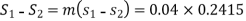
= 0.00966 kJ/K. (Ans.)
Q9. An iron cube at a temperature of 400°C is dropped into an insulated bath containing 10 kg water at 25°C. The water finally reaches a temperature of 50°C at steady state. Given that the specific heat of water is equal to 4186 J/kg K. Find the entropy changes for the iron cube and the water? Is the process reversible? If so why?
A9) Heat lost by iron cube = Heat gained by water
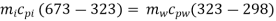
= 10  4186 (323 - 298)
4186 (323 - 298)
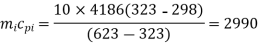
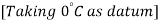
Entropy of iron at 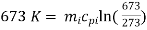

= 2697.8 J/K
Entropy of water at 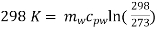
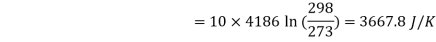
Entropy of iron at 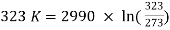 = 502.8 J/K
= 502.8 J/K
Entropy of water at 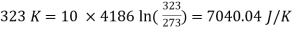
Changes in entropy of iron = 502.8 – 2697.8 = - 2195 J/K
Changes in entropy of water = 7040.04 – 3667.8 = 3372.24 J/K
Net change in entropy = 3372.24 – 2195 = 1177. 24 J/K
Since S > 0 hence the process is irreversible. (Ans.)
Q10) An insulated cylinder of volume capacity 4 m3 contains 20 kg of nitrogen. Paddle work is done on the gas by stirring it till the pressure in the vessel gets increased from 4 bar to 8 bar.
Determine:
(i) Change in internal energy,
(ii) Work done,
(iii) Heat transferred, and
(iv) Change in entropy.
Take for nitrogen: Cp = 1.04 kJ/kg K, and Cv = 0.7432 kJ/kg K.
A10) Pressure, 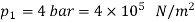
Pressure, 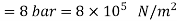
Volume, 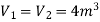
And it is constant for both end states.
Now, 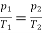
Or 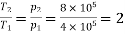
Also, R = cp – cv = 1.04 -0.7432 = 0.2968 kJ/kg K.
The mass of the gas in the cylinder is given by
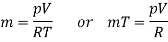
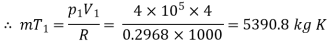
And 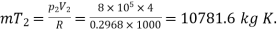
(i) Change in internal energy,
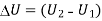
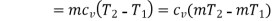
= 0.7432 (10781.6 – 5390.8) = 4006.4 kJ. (Ans.)
(ii) Work done, W :
Energy in the form of paddle work crosses into the system, but there is no change in system boundary or pdv work is absent. No heat is transferred to the system. We have
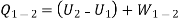
But 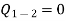
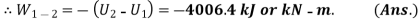
(iii) Heat transferred, 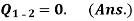
(iv) Change in entropy,