Unit 4
Geometric Transformation
Q1) Define geometric transformation. Give need and use of geometric transformation.
A1) “Geometric Transformation is the change of the orientation, shape and size of the geometric model in the database and graphic image in the computer graphics.”
Transformations are the operations applied to geometrical description of an object to change its position, orientation, or size are called geometric transformations.
Any two-dimensional graphic element or object is constructed out of points. Hence, transformation of any two-dimensional graphic element essentially means the transformation of all the points of geometric entity.
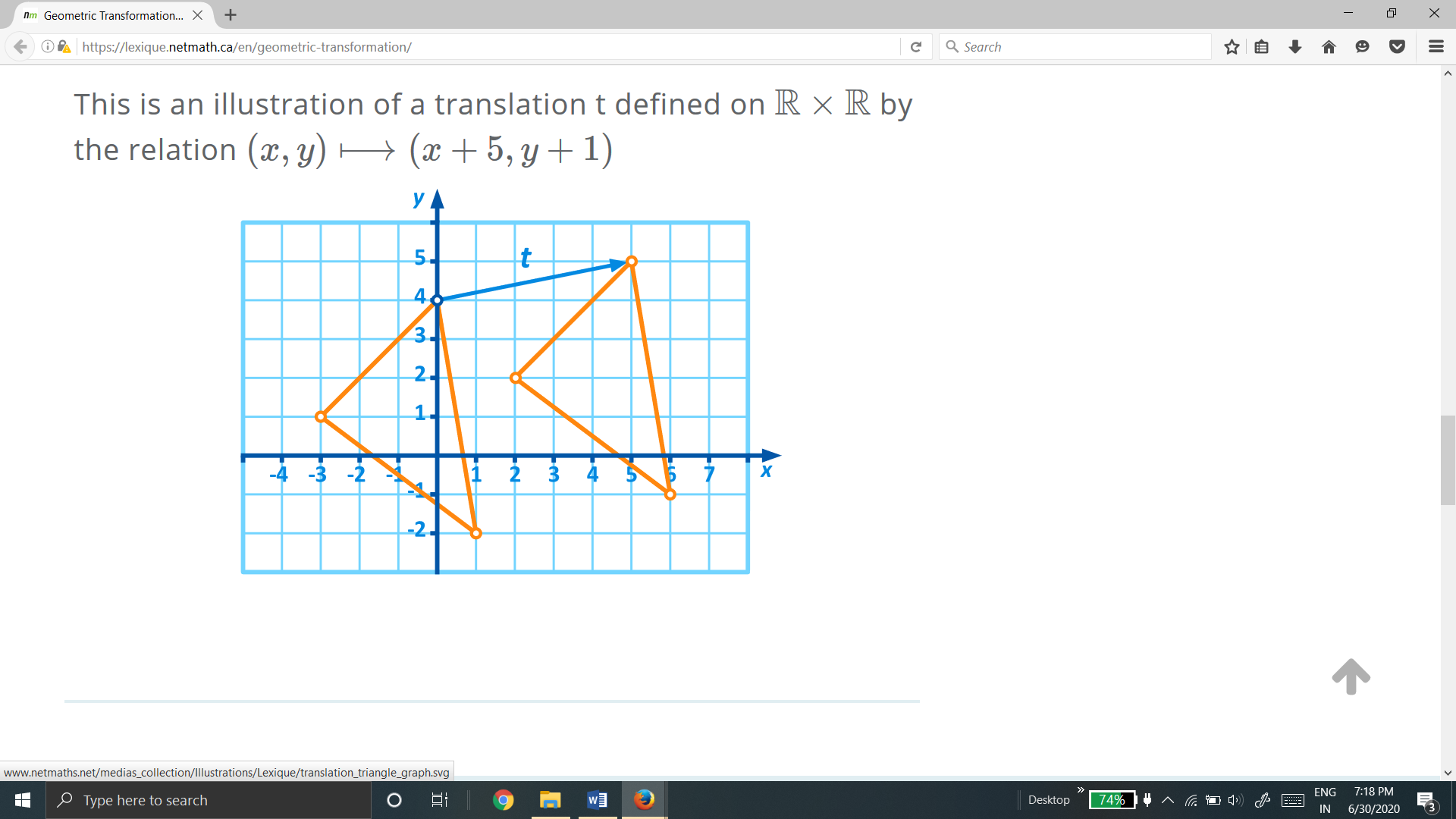
Geometric Transformation
Need of Geometric Transformation
Use of Geometric Transformation
The geometric transformations are used for following purposes:
Q2) Explain homogeneous representation.
A2) The rotation of a point, straight line or an entire image on the screen, about a point other than origin, is achieved by first moving the image until the point of rotation occupies the origin, then performing rotation, then finally moving the image to its original position.
The moving of an image from one place to another in a straight line is called a translation. A translation may be done by adding or subtracting to each point, the amount, by which picture is required to be shifted.
Translation of point by the change of coordinate cannot be combined with other transformation by using simple matrix application. Such a combination is essential if we wish to rotate an image about a point other than origin by translation, rotation and again translation.
To combine these three transformations into a single transformation, homogeneous coordinates are used. In homogeneous coordinate system, two-dimensional coordinate positions (x, y) are represented by triple-coordinates.
Homogeneous coordinates are generally used in design and construction applications. Here we perform translations, rotations, scaling to fit the picture into proper position.
To convert the coordinates of a 2D graphic element into homogeneous coordinates, the original coordinates are multiplied by a homogeneous parameter ‘h’ and the third coordinate is added whose value is the same parameter ‘h’.
Mathematically,

Where,
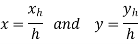
Hence, any 2 x 2 transformation matrix in two-dimensional cartesian system are modified to 3 x 3 transformation matrix in homogeneous coordinate system.
Q3) What is inverse transformation? Give transformation matrices for various inverse transformations.
A3) “These are also called as opposite transformations.”
If T is a translation matrix than inverse translation is representing using T-1. The inverse matrix is achieved using the opposite sign.
During the development of composite transformation matrix, many a times, it is necessary to use the inverse of some basic geometric transformation matrices.
Various Inverse Transformation matrices for various 2D Inverse geometric transformations are:
The inverse translation matrix is obtained by replacing the translation parameters 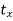 and
and 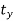 with
with 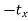 and
and 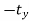 respectively in translation matrix.
respectively in translation matrix.
Therefore, inverse translation matrix is given as
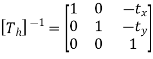
b. Inverse Rotation
The inverse rotation is obtained by the rotation parameter 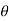 with
with 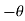 in rotation matrix.
in rotation matrix.
If rotation matrix rotates the graphic element in anticlockwise direction then inverse rotation rotates the graphic element in clockwise direction.
Therefore, the inverse rotation matrix is

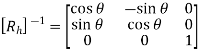
c. Inverse Scaling
The Inverse scaling matrix is obtained by replacing the scaling parameters 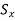 and
and 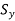 with
with 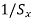 and
and  respectively in scaling matrix.
respectively in scaling matrix.
If Scaling matrix increases the size of the graphic element, then inverse scaling matrix reduces the size of graphic element.
Therefore, inverse scaling matrix is given by
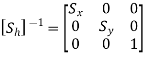
d. Inverse Reflection
The inverse reflection matrix is same as that of the reflection matrix.
Therefore,





Q4) Explain concatenated transformation with example.
A4) A concatenated transformation is the combination of two or more transformation such as: translation, rotation, scaling and reflection. A single transformation matrix, known as composite matrix or concatenated matrix can be obtained from such combination of transformations. This helps to improve the performance of graphic package.
The concatenated transformation of any graphic element is the concatenated transformation of all the points on that element.
Suppose we want to perform rotation about an arbitrary point, then we can perform it by the sequence of three transformations
The ordering sequence of these numbers of transformations must not be changed. The composite transformation is performed by multiplying matrix in order from right to left side.
Example showing composite transformations:
The enlargement is with respect to center. For this following sequence of transformations will be performed and all will be combined to a single one
Step1: The object is kept at its position as in fig (a)
Step2: The object is translated so that its center coincides with the origin as in fig (b)
Step3: Scaling of an object by keeping the object at origin is done in fig (c)
Step4: Again translation is done. This second translation is called a reverse translation. It will position the object at the origin location.

Mathematical representation of the composite transformation for the above example:
In the above example object is first translated.
Therefore, translation matrix is given by
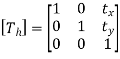
Let (a, b) be the centroid of the object(triangle)
In this case,
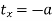
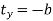
As the object is translated so that its centroid coincides with origin.
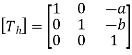
In the second step, the object is scaled by parameters Sx and Sy.
The scaling matrix is given by

And finally, the object is again translated back to its original position. It becomes an inverse translation
Inverse Translation matrix is given by

But
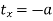
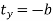
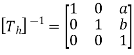
The concatenated transformation matrix is


And the transformation equation is
Q5) Explain Model coordinate system and Local coordinate system.
A5)
“The model coordinate system is the reference space of model with respect to which all the geometrical data of model is stored in database.”
This is the only coordinate system that modelling software recognizes when storing or retrieving the graphical information in or from model database.
The CAD software stores the graphical information in the model database with reference to the coordinate system known as model coordinate system.
The world coordinate system is a reference coordinate system used to describe what the world of interest looks like, as its name implies (i.e., what types of objects exist in the world and how they are located). For example, this system can be used to describe the locations and orientations of desks, chairs, and the blackboard if the world in which we have an interest is a classroom.
b. User Coordinate System (UCS) or Local Coordinate System or Working Coordinate System (WCS):
Now, to describe the shape of each object in that world. The shape of an object is defined by the coordinates of all the points or some characteristic points on the object with respect to a coordinate system attached to the object. This coordinate system is called the model coordinate system
“User Coordinate System is defined by the user for the convenience of input of the graphical information.”
In CAD modelling, the user inputs the graphical information with reference to the coordinate system known as user coordinate system.
If the geometric model has a complex geometry or a specific orientation, it is highly inconvenient to input the graphical data in a model coordinate system.
Figure below explains the difference between model coordinate system and local coordinate system.
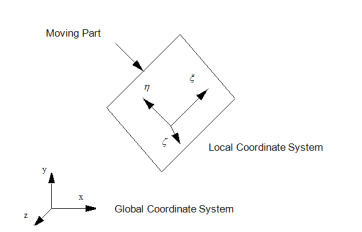
Model and User coordinate system
Q6) What is general mapping? Derive matrix for general mapping.
A6) “It is the combination of rotational and translational mapping.”
If both the coordinate systems don’t have common origin and the axes are at an angle, then the mapping is called general mapping.
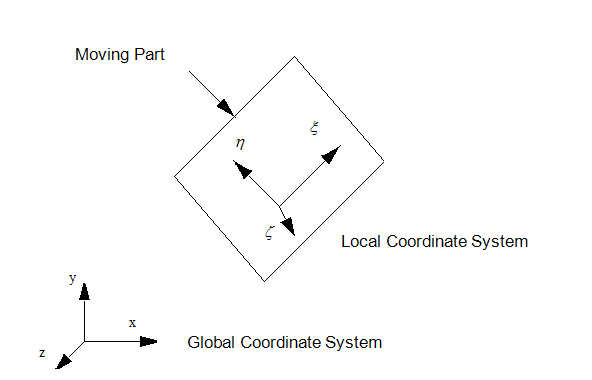
Let, dx= distance of the origin of original system (O) from the origin of the new coordinate system (O’) along X-direction.
dy= distance of the origin of original system (O) from the origin of the new coordinate system (O’) along Y-direction.
ɸ = angle made by the axes of original coordinate system with the axes of new coordinate system.
Coordinate of point P in new coordinate system are:
x’ = x cos ɸ - y sin ɸ + dx
y' = x sin ɸ + y cos ɸ + dy
The above equation in matrix form can be written as
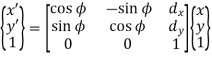
Or
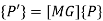
Where,
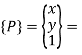 Coordinates of point P in original coordinate system X-Y
Coordinates of point P in original coordinate system X-Y
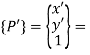 Coordinates of point P in new coordinate system X’-Y’
Coordinates of point P in new coordinate system X’-Y’
 General mapping matrix
General mapping matrix
Q7) Write a note on Parallel projection. Explain its types.
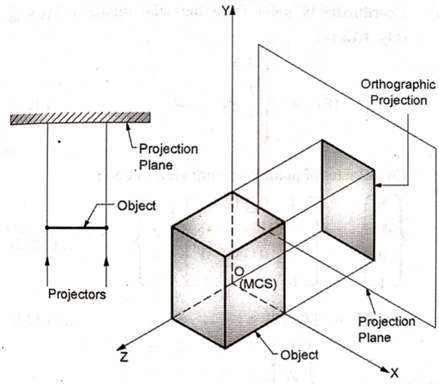
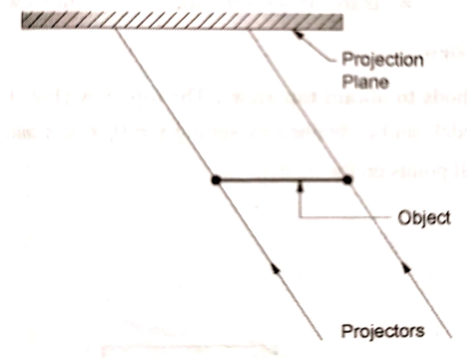
A7) If the center of projection is at infinite distance from the projection pane, all the projections are parallel to each other. Such method of projection is called as parallel projection.

Parallel projection
Parallel Projection use to display picture in its true shape and size.
The parallel projection are further classified into two types:
In orthographic projection all the projectors are parallel to each other and perpendicular to projection plane.
In this method of projection, one of the principal axes of MCS of the object is perpendicular to the projection plane, while remaining two principal axes are parallel to the projection plane.

Orthographic projection
b. Axonometric or oblique projection
In axonometric projection all the projectors are parallel to each other and inclined to projection plane.
In this method of projection, the principal axes of MCS of the object are inclined to the projection plane. Therefore, axonometric projection shows several faces of model at one glance.
Axonometric projection
Some of the axonometric projections are
Dimetric: In these two projectors have equal angles. With respect to two principle axes.
Trimetric: The direction of projection makes unequal angle with their principle axes.
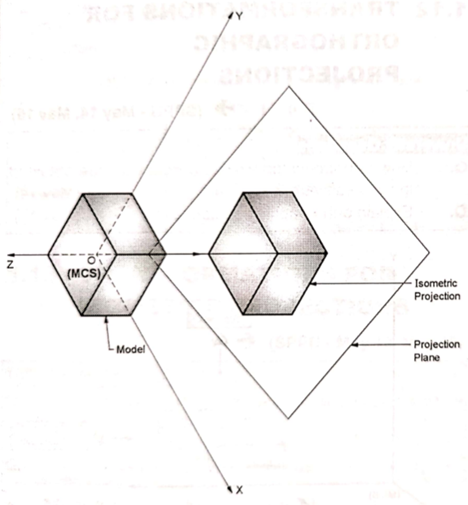
But the most commonly used axonometric projection is an isometric projection.
Isometric projection
In isometric projection, the projection planes intersect each principal axis of MCS of the object at the same distance from the origin. All projectors make equal angles generally angle is of 30°.
Isometric projection
Q8) Write a note on perspective projection.
A8) If the center of projection is at finite distance from the projection plane, all the projectors meet at the center of projection and they are non-parallel. Such a method of projection is called perspective projection.
Perspective projection
In perspective projection, farther away the object from the viewer is, smaller it appears. This property of projection gives an idea about depth. The artist use perspective projection from drawing three-dimensional scenes.
Two main characteristics of perspective are vanishing points and perspective foreshortening. Due to foreshortening object and lengths appear smaller from the center of projection. More we increase the distance from the center of projection, smaller the object will appear.
The perspective projection helps in adding an artistic effect and enhancing realism to the projected view.
Vanishing Point:
“It is the point where all lines will appear to meet. There can be one point, two point, and three-point perspectives.”
One Point:
“There is only one vanishing point.”
Two Points:
“There are two vanishing points. One is the x-direction and other in the y –direction.”
Three Points:
“There are three vanishing points. One is x second in y and third in two directions.”
In Perspective projection lines of projection do not remain parallel. The lines converge at a single point called a center of projection. The projected image on the screen is obtained by points of intersection of converging lines with the plane of the screen. The image on the screen is seen as of viewer's eye were located at the center of projection, lines of projection would correspond to path travel by light beam originating from object.

Q9) If a point P having coordinates (3,3) is mirrored about X and Y axis, determine new coordinates.
A9)
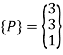
Mirror about both axis means mirror about origin.

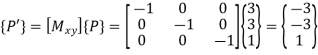
The new coordinates of point are (-3,-3).
Q10) An object is to be rotated about point A(-10,-10) by 90o in anti-clockwise direction. Find the concatenated transformation matrix.
A10)
A(-10,-10) 
The rotation about point A(-10,-10) through  can be achieved in three steps:
can be achieved in three steps:
Translate the line such that, point A coincides with origin. Hence translation distances are:
tx = 10 and ty = 10

2. Rotation
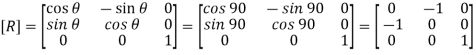
3. Inverse translation
Translate the line again at point A
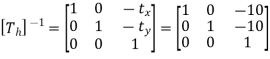
Concatenated matrix [CT]


Q11) A line drawn between P1(2,4) and P2(6,8), is rotated by 30o in CCW direction about point P1. Find the concatenated matrix and new coordinates of the points on the line.
A11)
P1(2,4) P2(6,8) and 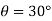
The rotation about point P1(2,4) through 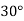 can be achieved in three steps:
can be achieved in three steps:
Translate the line such that, point P1 coincides with origin. Hence translation distances are:
tx = -2 and ty = -4
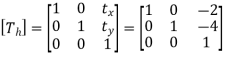
2. Rotation
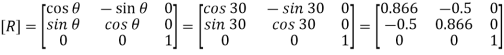
3. Inverse translation
Translate the line again at point A
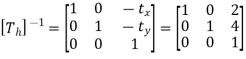
Concatenated matrix [CT]
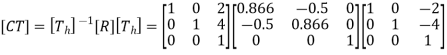

The new position of the line:
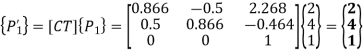
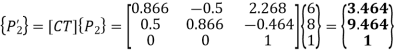
The new coordinates of the vertices of the rotated line are P’1 (2,4) and P’2 (3.464,9.464)
Q12) A triangle defined by points P (2,2) Q(6,2) R(4,4) is created in UCS having x-axis oriented at 45o and located at (4,5) units from MCS. Find coordinates of triangle in MCS.
A12) dx = 4 dy = 5 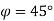 P(2,2) Q(6,2) R(4,4)
P(2,2) Q(6,2) R(4,4)
General mapping matrix is

Coordinates of vertices of triangle in MCS:

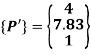

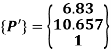

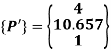
The coordinates of the triangle in MCS are:
P’(4,7.83), Q’(6.83,10.657) and R’(4,10.657)