Unit - 2
Fluid Statics
Q1) Define Hydrostatics with the help of diagram and also state the applications of it.
A1) To determine pressure at any point in a fluid at rest ‘hydrostatic law’ is used which states that ‘the rate of increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point.

Let p = Intensity of pressure on face LM,
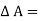 Cross sectional area of the element,
Cross sectional area of the element,
Z = Distance of the fluid element from free surface,
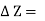 Height of the element,
Height of the element,
The forces acting on the elements are:
Pressure force on the face LM = p x 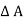 …….acting downward.
…….acting downward.
Pressure force on the face ST = 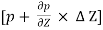 x
x 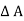 ……. Acting upward
……. Acting upward
Weight of the fluid element = Weight density x Volume
= w x  x
x 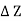
Pressure forces on the face MT & LS are equal and opposite.
For equilibrium of the fluid element,
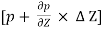 x
x 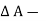 p x
p x 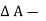 w x
w x 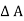 x
x 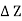 = 0
= 0
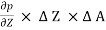 - w x
- w x 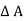 x
x 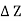 = 0
= 0
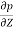 = w
= w
Above eqn states that rate of increase of pressure in a vertical direction in equal to weight density of the fluid at that point. This is hydrostatic law.
On integrating above eqn
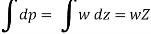
where p = pressure above atmospheric pressure
Z = pressure head.
w = Specific weight of liquid.
Application of the basic equation of hydrostatics
Q2) Explain the concept of Pressure head and explain the types of Measurement of pressure
A2) To determine pressure at any point in a fluid at rest ‘hydrostatic law ‘ is used which states that ‘the rate of increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point.
p = w Z
or
Z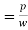
where p = pressure above atmospheric pressure
Z = pressure head.
w = Specific weight of liquid.
Measurement of pressure
Air exerts a normal pressure upon all surfaces with which it is in contact, and it is known as atmospheric pressure.
The atmospheric pressure is also known as Barometric pressure.
It is the pressure, measured with the help of pressure measuring instrument, in which the atmospheric pressure is taken as datum.
The atmospheric pressure on the scale is marked as zero.
It is necessary to establish as absolute pressure scale which is independent of the changes in atmospheric pressure.
A pressure of absolute zero can exist only in complete vacuum
Any pressure measured above the absolute zero of pressure is termed as an absolute pressure.
Q3) Explain Manometers Explain any 3 types of manometer?
A30 Manometer
Manometer are defined as the devices used for measuring the pressure at a point in a fluid by balancing the column of fluid by the same or another column of liquid.
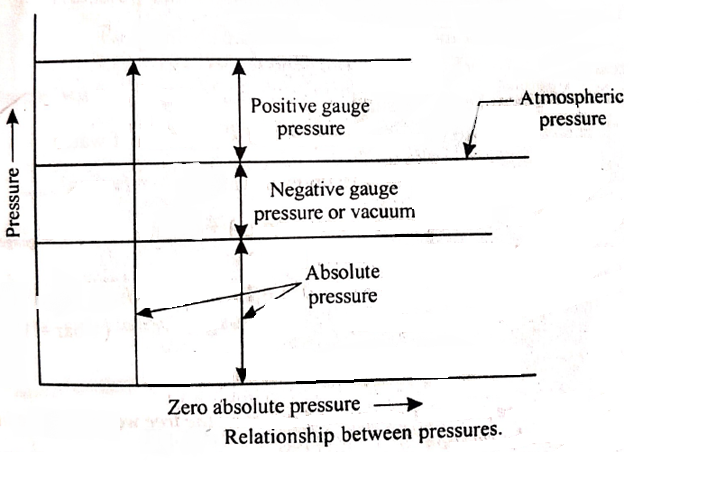
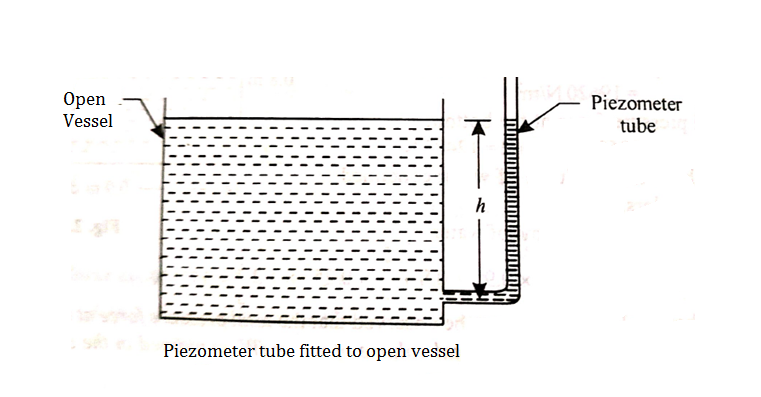
A “simple manometer” is one which consists of a glass tube whose one end is connected to a point where pressure is to be measured and the other end remains open to atmosphere.
ii. U-tube monometer:
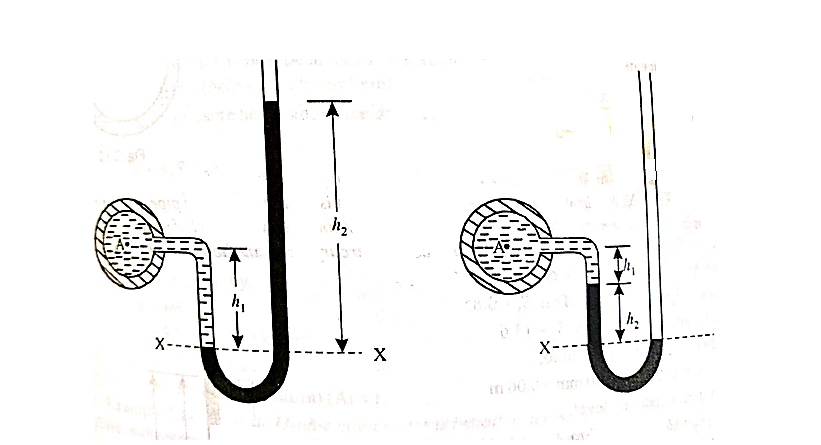
Fig (a) Fig (b)
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above X-X line in the left limb = h+h1S1
Pressure head above X-X in the right limb = h2S2
Equating these two pressures, we get
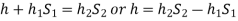
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb= 
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
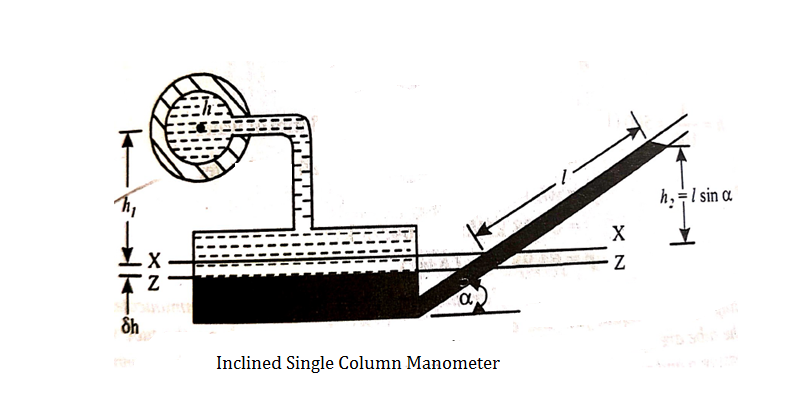
iii. Inclined Single Column Manometer:
l = length of the heavy liquid moved in right limb,
 = inclination of right limb horizontal, and
= inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin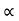
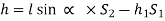
Q4) Explain Differential Manometers in Detail with the help of diagram.
A4) Differential Manometers
A differential manometer is used to measure the difference in pressures between two points in a pipe or in two different pipes.
1. U-tube differential manometer:
A U-tube differential manometer is shown in fig.
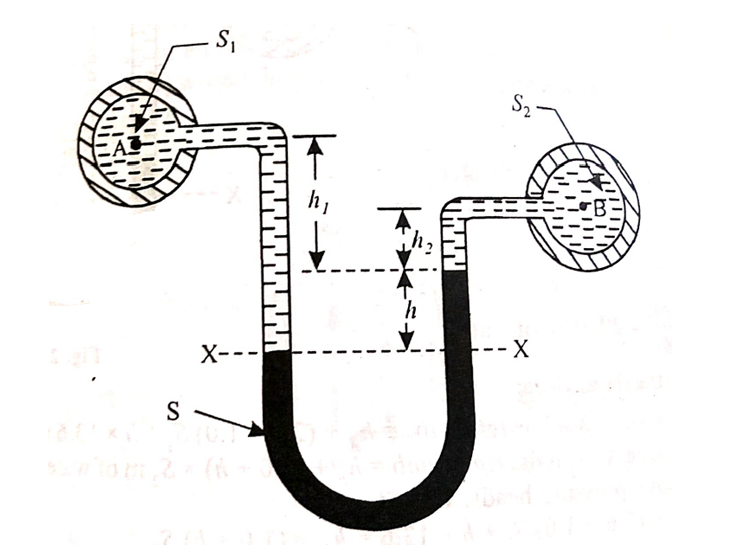
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the centre of A, from the mercury level in the left limb
h2 = distance of the centre of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
hA = pressure head at A,
hB = pressure head at B
considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
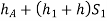
Pressure head in the right limb:
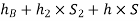
Equating the above pressure heads, we get
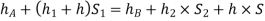
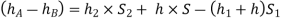
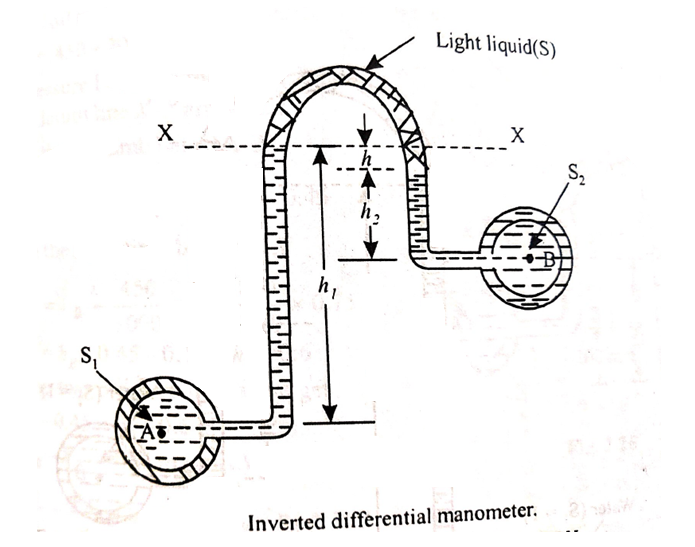
2. Inverted U-tube differential manometer:
A inverted U-tube differential manometer is shown in fig.
It consist of an inverted U tube, containing light liquid, whose two ends are connected to the points whose difference pressures is to be measured.
*95\\\\\\\\\\\
Let, h = difference of mercury level (light liquid) in the U-tube,
h1 = Height of liquid in the left limb below the datum line X-X
h2 = Height of liquid in the right limb below the datum line X-X
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of light liquid
hA = pressure head at A,
hB = pressure head at B
considering the pressure heads below the datum line x-x, we get
Pressure head in the left limb:
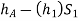
Pressure head in the right limb:
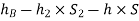
Equating the above pressure heads, we get
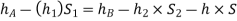
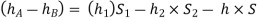
Q5) Explain in detail different types of Mechanical gauges.
A5) Mechanical Gauges
Bourdon tube pressure gauge:

Diaphragm Gauge:
Vacuum gauge:
Q6) what is total pressure? Explain in detail 2 cases of centre of pressure.
A6) Total Pressure
Total pressure is defined as the force exerted by a static fluid on a surface either plane or curved when the fluid comes in contact with the surfaces. This force always acts normal to the surface.
Centre of Pressure
Centre of pressure is defined as the point of application of the total pressure on the surface. There are four cases of submerged surfaces on which the total pressure force and centre of pressure is to be determined. The submerged surfaces may be:
Vertical and horizontal plane surface
Consider a thin horizontal strip of the surface of thickness dx and breadth b.
Let the depth of the strip be x.
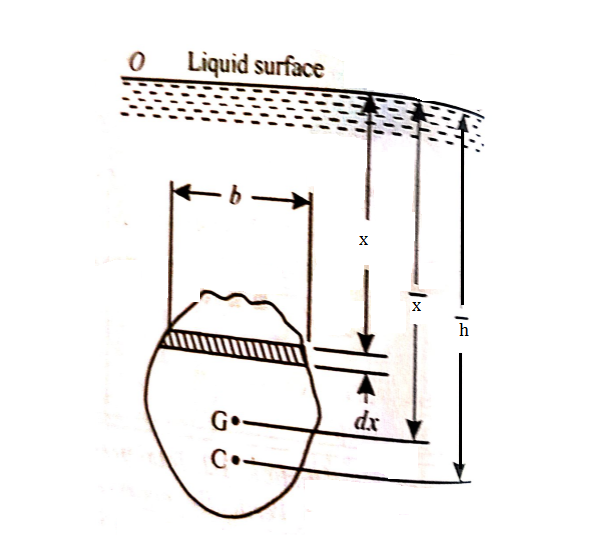
Let the intensity of pressure on strip be p.
p =wx
Total pressure on the strip = p.bdx = wx.bdx
Total pressure on the whole area P =
=w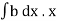
But 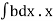 = Moment of the surface area about the liquid level = A
= Moment of the surface area about the liquid level = A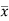
P=wA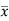
Moment of the pressure about free surface OO = (w.x.b. dx).x = w.x2.b.dx
Total Moment, M = 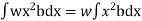
But 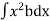 = Moment of inertia of the surface about free surface OO (I0)
= Moment of inertia of the surface about free surface OO (I0)
Hence, M = wI0
The sum of the moment of the pressure is also equal to P×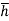 .
.
P× = wI0
= wI0
wA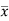 x
x 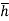 = wI0
= wI0
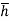 =
= 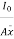
But 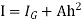
Above eqn becomes
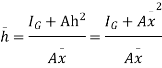
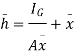
Q7) Explain in detail Inclined surface, curved surface cases of center of pressure.
A7)
Inclined plane surface
Let A = area of the surface
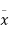 = depth of the centre of gravity from the free liquid surface.
= depth of the centre of gravity from the free liquid surface.
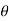 =angle at which the immersed surface is inclined with the liquid surface.
=angle at which the immersed surface is inclined with the liquid surface.
w=specific weight of liquid.
Consider a strip of thickness dx width b at a distance l from O.
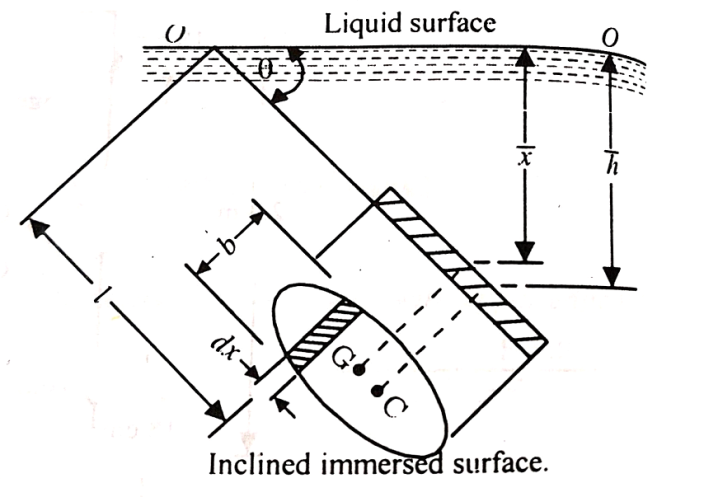
The intensity of pressure on the strip = wlsin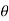
Area of strip = bdx
Pressure on the strip =Intensity of pressure × area = wlsin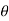 × b.dx
× b.dx
Total pressure on the surface
P = 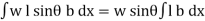
But 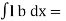 Moment of surface about OO =
Moment of surface about OO = 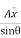
P=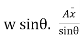 = w.
= w.
Let, 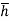 = Depth of centre of pressure below free liquid surface
= Depth of centre of pressure below free liquid surface
IG = Moment of inertia of the immersed surface about 00.
Moment of pressure about OO = wl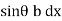 × l = wl2
× l = wl2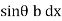
Sum of moments about O
M = 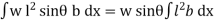
But 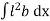 = I0 = Moment of inertia of the surface about point O
= I0 = Moment of inertia of the surface about point O
M =  Io
Io
Sum of moment of all such pressure about O is also equal to 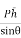
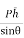 = w
= w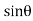 Io
Io
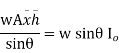
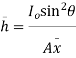
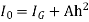
Where 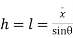
 (
(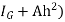
=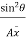 (
( 2)
2)
= +
+ 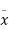
Curved surface
Consider a curved immersed surface LM submerged in a static fluid as shown in fig.
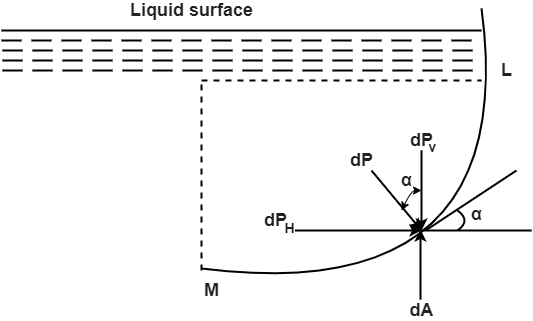
At any point on the curved surface, the pressure acts normal to the surface.
Thus, if dA is the area of a small element of the curved surface lying at a vertical depth of h from surface of the liquid, then total pressure on the elemental area is
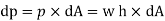
This force dP acts normal to the surface. Further integration of above eqn would provide the total pressure on the curved surface and hence

But in case of curved surface the direction of the total pressure on the elementary areas are not in the same direction but varies from point to point.
Thus, the integration of eqn. for curved surface is impossible. The problem however, can be solved by resolving the force P into horizontal and vertical components PH and PV. Then total force on the curved surface is
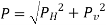
Hence, the direction of the resultant force P
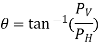
Where,
PH = Total pressure force on the projected area of the curved surface on vertical plane.
PV = Weight of the liquid supported by the curved surface of liquid.
Q8) Define Buoyancy. What are the principles of flotation?
A8) Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force which tends to lift it up.
The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to action of gravity is known as buoyancy.
The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
The magnitude of the buoyant force can be determined by Archimedes principle which states as follows:
“When a body is immersed in a fluid either wholly or partially it is buoyed or lifted up by a force which is equal to the weight of fluid displaced by the body. ”
Centre of Buoyancy
The point of application of the force of buoyancy on the body is known as the center of buoyancy. It is always the center of gravity of the volume of fluid displaced.
Q9) Define Stable, natural and unstable equilibrium.
A9) Stability of floating Body:
The stability of a floating body is determined from the position of Meta-centre (M).
a) Stable Equilibrium
If the point M is above G, the floating body will be in stable equilibrium as shown in Fig.
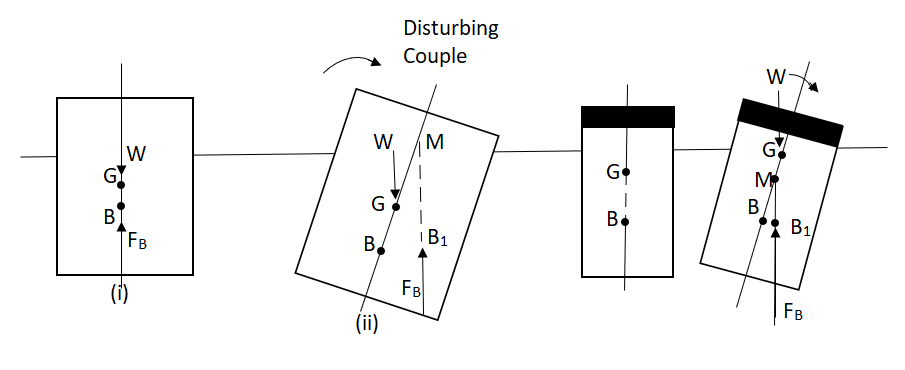
M is above G (stable equilibrium) M is below G (unstable equilibrium)
If a slight angular displacement is given to the floating body in the clockwise direction, the center of buoyancy shifts from B to B1, such that the vertical line through B1 cuts at M.
Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti-clockwise direction and thus bringing the floating body in the original position.
Unstable Equilibrium:
If the point M is below G, the floating body will be in unstable equilibrium as shown in fig.
The disturbing couple is acting in the clockwise direction.
The couple due to buoyant force FB and W is also acting in clock direction and thus overturning the floating body.
Neutral Equilibrium:
If the point M is at the center of gravity of the body. The floating body will be in neutral equilibrium.
Q10) Define stability of submerged body.
A10) Stability of submerged Body:
The position of center of gravity ¢er of buoyancy in case of a completely submerged body are fixed.
Weight W acting vertically downward through G, while the buoyant force FB is acting vertical up through B.

Stable Equilibrium
When W = FB& point B is above G, the body is said to be in stable equilibrium.
Unstable Equilibrium:
If W = FB, but center of buoyancy B is below the center of gravity G, the body is in unstable equilibrium.
Neutral Equilibrium:
If W = FB & point B & G are at the same point, the body is said to be in neutral equilibrium.
Q11) Define Meta center and explain with the help of diagram.
A11) It is defined as the point about which a floating body starts oscillating when the body is tilted by a small angle.
The meta-center may also be defined as the point at which the line of action of the force of buoyancy will meet the normal axis of the body when the body is given a small angular displacement.
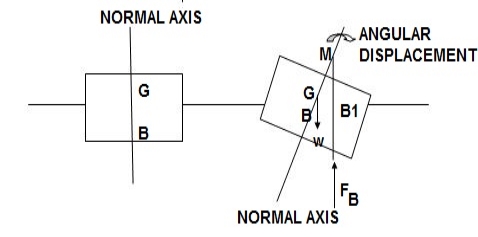
Consider a body floating in a liquid as. Let the body is in equilibrium and G is the center gravity and B is the center of Buoyancy.
Let the body is given a small angular displacement in the clockwise direction as shown in fig. the center of buoyancy, which is the center of the displaced liquid or center of gravity of portion of the body submerged in liquid, will be shifted towards right from the normal axis.
Let it is at B1 as shown in Fig.
The line of action of the force of buoyancy in this position, will intersect the normal axis of the body some point say M.
This point M is called Meta-center.
Q12) Determine the Metacentric height? (Analytical method)
A12) Analytical method

Let the area of this elementary prism be  A.
A.
The height of this elementary prism is given by x.Ө
The volume of this elementary prism is given by

The upward force or buoyancy for acting at this prism (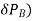 is given by
is given by
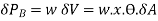
The moment of this buoyancy force about O
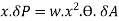
For the total portion N’ON, this moment is given by
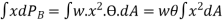
Or 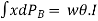
Where I = moment of inertia of the sectional area at the waterline about the axis through O.
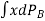 gives the change in moment due to buoyancy.
gives the change in moment due to buoyancy.
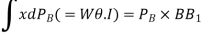
(Where PB = the total force of buoyancy)
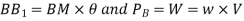
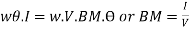
Now metacentric height, GM=BM  BG
BG
Q13) Determine the Metacentric height? (Experimental method)
A13) Experimental model

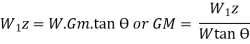
If, l = length of plumb bob, and
d = displacement of the plumb bob,
then, 
and metacentric height is given by,
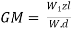
Q14) A rectangle plane surface is 2 m wide & 3 m deep. It lies in vertical plane in water. Determine the total pressure & position of center of pressure when its upper edge is horizontal & a) Coincides with water surface b) 2.5 m below the free water surface.
A14) Given
b = 2m
d = 3m
a). Upper edge coincides with water surface
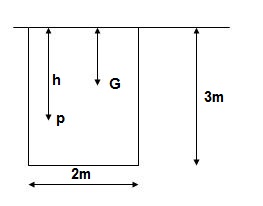
A = b x d = 2 x 3 = 6 m2
X = d/2 -3/2 = 1.5 m
Total Pressure
F = AX
= 9810 x 6 x 1.5
= 88290 N
IG = bd3/12 = 2 x 33/12 = 4.5 m4
Centre of Pressure
h = IG/AX + X = 4.5/ (6 x 1.5) + 1.5 = 2m
b). Upper edge 2.5 m below water surface
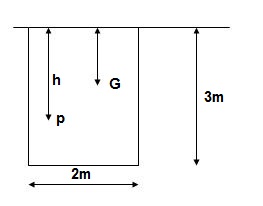
X = 2.5 + 3/2 = 4m
Total pressure F = Ax
= 9810 x 6 x 4
= 235440 N
h = IG/AX + X = 4.5/(6 x 4) + 4 = 4.1875 m
Q15) A heavy car plunges into a lake during an accident & land at the bottom of the lake on its wheel. The door is 1.2 m high & 1m wide, the top edge of the door is 8m below the free surface of the water. Determine total pressure acting on door approximating it as a vertical rectangular plate & center of pressure.
A15) Given
b = 1 m
d = 1.2 m
A = b x d = 1 x 1.2 = 1.2 m2
X = 8 + d/2 = 8 + 1/2/2 = 8.6 m
F = AX
= 9810 x 1.2 x 8.6
= 101.24 x 103 N
IG = bd3/12 = 1 x 1.23/12 = 0.144 m4
h = IG/AX + X = 0.144/(1.2 x 8.6) + 8.6 = 8.614 m
Q16) A circular plate 1.5 m diameter is submerged in water with its greatest & least depth below the surface being 2 m & 0.75 m respectively. Determine total pressure & center of pressure.
A16) Given
d = 1.5 m

1). A = π/4 x d2 = π/4 x 1.52 = 1.767 m2
2). X = Greatest depth + Least depth / 2
= (2 + 0.75)/2 = 1.375 m
3). F = AX
= 9810 x 1.767 x 1.375
= 28.83 x 103 N
4). Sin = 1.25/1.5 = 0.833
5). IG = π/64 x d4 = π/64 x 1.54 = 0.248 m4
6). h = IG Sin2/AX + X
0.248 x 0.8332/1.767 x 1.375 + 1.375
= 1.446 m
Q17) A triangular plate of 1m base & 1.5 m altitude is immersed in water. The plate is inclined at 300 with free water surface & base is parallel to & at a depth of 2 m from water surface. Find total pressure & center of pressure.
A17) Given
b = 1 m
h = 1.5 m
= 300
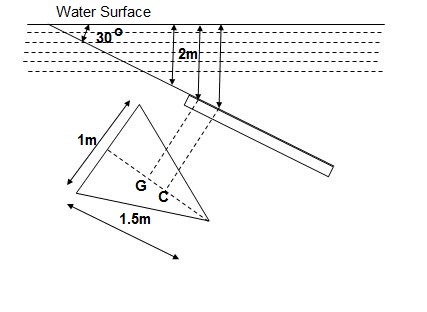
A = ½ x b x h = ½ x 1 x 1.5 = 0.75 m2
X = 2 + 1.5/3 x Sin 30 = 2.25 m
F = AX
= 9810 x 0.75 x 2.25
= 16.55 x 103 N
IG = bh3/36 = 1 x 1.53/36 = 0.09375 m4
h = IGSin2/AX + X
= 0.09375 x (Sin 30)2/0.75 x 2.25 + 2.25
= 2.264 m
Q18) A solid cylinder of diameter 4m and height 4 m. find the metacentric height of the cylinder if the specific gravity of cylinder is 0.6 and it is floating in water with its axis vertical. State whether the equilibrium is stable or unstable.
A18) D=4m
H=4m
S=0.6

Depth of cylinder in water = 0.6H = 0.6(4) = 2.4m
Distance of center of buoyancy(B) from A
AB = 2.4 / 2 = 1.2m
Distance of center of gravity (G) from A
AG = H / 2 = 2m
BG = AG – AB = 2 – 1.2 = 0.8m
I = 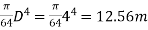 4
4
V = Volume of cylinder in water
=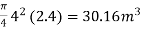
Metacentric height GM = (I / V) – BG
= (12.56/30.16) – 0.8
= -0.383 m
Negative sign means that the meta centre M is below the centre of gravity G. Thus, the cylinder is in unstable equilibrium.
Q19) A differential manometer is connected to at two points A and B of two pipes as shown in fig. Pipe A contains liquid of specific gravity 1.6, while pipe B contains liquid of specific gravity 0.8. If the pressure at A and B are 11.8×10⁴ N/m² and 19.60× 10⁴ N/m², find the difference in Mercury level in differential manometer.
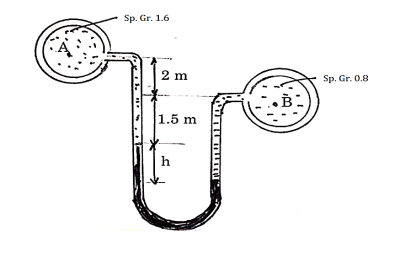
A19) S1 =1.6
S2 = 13.6
S3 = 0.8
PA = 11.8 ×10⁴ N/m²
PB =19.60× 10⁴ N/m²
h1 = 3.5m h2 = h h3 = h+1.5
PB – PA = w (hB – hA)
19.60× 10⁴ - 11.8 ×10⁴ = 9810 (hB – hA)
hB – hA= 7.95m
Pressure in left limb above datum line = Pressure in right limb above datum line
hA+h1s1+h2s2 = hB+h3s3
h1s1+h2s2-h3s3 = hB - hA
3.5×1.6+h (13.6)- (h+1.5)0.8 = 7.95
h = 0.28m
Q20) An inverted differential manometer having an oil of specific gravity 0.75 was connected to two different types carrying water under pressure as shown in figure. Determine the pressure in the pipe B in terms of kPa, if manometer reads as shown in figure. Take pressure in the pipe A as 1.5 m of water.
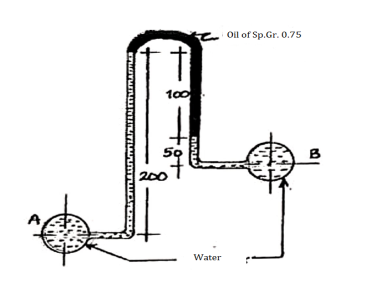
A20) S1 =1 S2=0.75 S3=1
h1=0.2m h2=0.1m h3=0.05m hA=1.5m
Pressure in left limb below datum line = Pressure in right limb below datum line
hA - h1s1 = hB - h2s2-h3s3
1.5 – 0.2×1 = hB - 0.1×0.75-0.05×1
HB = 1.425m
PB = whB = 9810 ×1.425 = 13979.25 N/m2