Unit - 3
Fluid Kinematics
Q1) Define fluid kinematics? Explain 1 method of motion of fluid.
A1) Ans Fluid kinematics is a branch of ‘Fluid Mechanics’ which deals with the study of velocity and acceleration of the particles of fluid in motion and then distribution in space without considering any force or energy involved.
Methods of describing the motion of fluid
Lagrangian method
In this method, the observer concentrates on the movement of a single particle.
The path taken by the particle and the changes in its velocity and acceleration are studied.
In the cartesian system the position of the fluid particle in space (x, y, z) at any time t from its position (a, b, c) at time t=0 shall be given as,
x = f1(a, b, c, t)
y = f2(a, b, c, t)
z = f3(a, b, c, t)
The velocity and acceleration components (obtained by taking derivations with respect to time) are given by,
u = 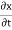
velocity components: v = 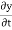
w = 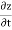
ax = 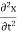
acceleration component: ay = 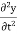
az = 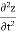
At any point, the resultant velocity or acceleration shall be the resultant of these components of the respective quantity at that point.
Resultant velocity, v = 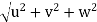
Acceleration a = 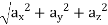
Similarly, other quantities like pressure, density, etc. can be found.
Q2) Explain the Eulerian method of motion of fluid.
A2) Eulerian Method
In Eulerian method, the observer concentrates on a point in the fluid system. Velocity, acceleration and other characteristics of the fluid at that particular point are studied.
This method is almost exclusively used a fluid mechanics, especially because of its mathematical simplicity. The velocity at any point (x, y, z) can be written as
u = f1(x, y, z, t)
v = f2(x, y, z, t)
w = f3(x, y, z, t)
The components of acceleration of the fluid particle can be worked out by partial differentiation as follows:
ax = 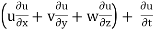
ay = 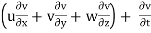
az = 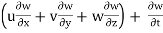
Now, resultant velocity: v = 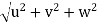
Acceleration a = 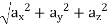
Q3) Define Stream line, stream tube, path line & streak line & control volume
A3) Streamline
A streamline may be defined on as an imaginary line within the flow so that the tangent at any point on it indicates the velocity at that point.
Stream tube
A stream tube is a fluid mass bounded by a group of streamlines. The contents of stream tube are known as current filament. Examples: Pipes & nozzles.
Path line
A path line is the path followed by a fluid particle in motion. A path line shows the direction of particular particle as it moves ahead.
Streak line
A streak line is a curve which gives an instantaneous time picture of the location of the fluid particles, which have passed through a given point.
E.g.: the path taken by smoke coming out of chimney.
The velocity potential is defined as a scalar function of space and time such that its negative derivative with respect to any direction given the fluid velocity in that direction.
Control volume
A definite volume with fixed boundary shape in space along with fluid flow passage is called control volume & the boundary of his volume is known as the control surface.
Boundary of control volume may be extended up to such an extent that it includes the portion of the flow passage which is to be studied.
Q4) Classify the different types of flow.
A4) Steady and Unsteady flows
Steady flow – The type of flow in which the fluid characteristics like velocity, pressure, density, etc. at a point do not change with time is called steady flow.
Example: Flow through a prismatic or non-prismatic conduct at a constant flow rate Q m3/s is steady.
Mathematically, 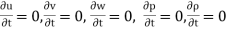
Unsteady flow: It is that type of flow in which the velocity, pressure or density at a point change w. r. t. time.
E.g.: the flow in a pipe whose value is being opened or closed gradually.
Mathematically, 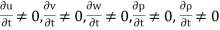
Uniform and Non-uniform Flows
Uniform flow – The type of flow, in which the velocity at any given time does not change with respect to space is called uniform flow.
E.g.: Flow through a straight prismatic conduit.
Mathematically, 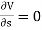 when t = constant
when t = constant
Non-uniform flow – It is that type of flow in which the velocity at any given time changes with respect to space.
E.g.: Flow through non-prismatic conduit.
Mathematically, 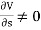 when t = constant
when t = constant
One, two & Three-dimensional flow
One dimensional flow – it is that type of flow in which the flow parameter such as velocity is a function of time and one space coordinate.
E.g.: Flow in a pipe where average flow parameters are considered for analysis.
Mathematically, u = f(x), v = 0 & w = 0
Two-dimensional Flow – The flow in which the velocity is a function of time and two rectangular space coordinates is called two-dimensional flow.
E.g.: Flow between parallel plates of infinite extent.
Mathematically, u = f1(x, y) v = f2(x, y) & w = 0
Three-dimensional flow – It is that type of flow in which the velocity is a function of time and three mutually perpendicular directions.
E.g.: Flow in a converging or diverging pipe or channel.
Mathematically, u = f1(x, y, z) v = f2(x, y, z) & w = f3(x, y, z)
Rotational and Irrotational Flows
Rotational Flow -A flow said to be rotational if the fluid particles while moving in the direction of flow rotate about their mass centers.
E.g.; Motion of liquid in a rotating tank.
Irrotational flow - A flow said to be rotational if the fluid particles while moving in the direction of flow do not rotate about their mass centers.
E.g.: Flow above a drain hole of a stationary tank or a water basin.
Laminar and Turbulent Flows
Laminar Flow – A Laminar flow is one in which paths taken by the individual particles do not cross one another and move along well-defined path.
E.g.: Flow of blood in veins and arteries.
Turbulent Flow – A turbulent flow is that flow in which fluid particles move in a zig zag way.
E.g.: High velocity flows in conduit of large size.
Compressible & Incompressible Flow
Compressible Flow – It is that type of Flow in Which the density (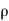 ) of the fluid changes from point to point.
) of the fluid changes from point to point.
E.g.: Flow of gases through orifices, nozzles, gas turbines, etc.
Mathematically, 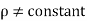
Incompressible Flow – It is that type of flow in which density is constant for the fluid flow. Liquids are generally considered flowing incompressible.
E.g.: subsonic aerodynamics.
Mathematically, 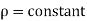
Subcritical, Critical & Supercritical Flow
Subcritical flow– When Froude’s number is less than one the flow is known as subcritical flow.
Mathematically, Fr 
Critical flow– When Froude’s number is equal to one the flow is known as subcritical flow.
Mathematically, Fr 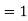
Supercritical flow– When Froude’s number is more than one the flow is known as subcritical flow.
Mathematically, Fr 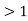
Q5) Derive the continues equation for three-dimensional flow in Cartesian co-ordinates.
A5) Considers a fluid element (control volume)- parallelepiped with sides dx, dy and dz as shown in fig.
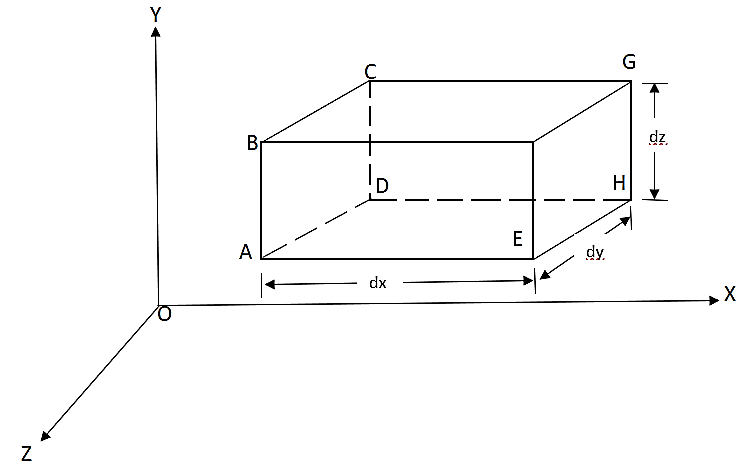
Let, 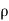 = Mass density of the fluid at a particular instant
= Mass density of the fluid at a particular instant
u, v, w= components of velocity of flow entering the three faces of the parallelepiped.
Rate of Mass of fluid entering the face ABCD
= 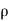 X velocity in x-direction X area of ABCD
X velocity in x-direction X area of ABCD
=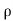 u dy dz
u dy dz
Rate of Mass of fluid leaving the lace FEGH
= 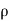 u dy dz +
u dy dz + 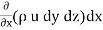
:. Mass accelerated per unit time, due to flow in x-direction
= 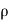 u dy dz – [
u dy dz – [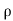 u+
u+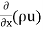 dx] dy dz
dx] dy dz
= - -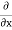 (
(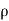 u) dx dy dz
u) dx dy dz
Similarly, the gain in fluid mass per unit time in the parallelepiped due to flow in Y and Z- direction.
= 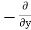 (
(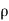 v) dx dy dz ……… (in Y- direction)
v) dx dy dz ……… (in Y- direction)
= 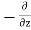 (
(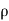 w) dx dy dz ……… (in Z- direction)
w) dx dy dz ……… (in Z- direction)
The, total gain in fluid mass per unit for fluid along three co-ordinate axes
= - [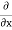 (
(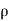 u) +
u) +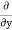 (
(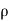 v) +
v) + 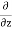 (
(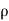 w)] dx dy dz …………1
w)] dx dy dz …………1
Rate of change of mass of the parallelepiped (control volume)
= 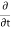 (
(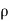 dx, dy dz) …………………. 2
dx, dy dz) …………………. 2
From Equation 1& 2
- [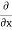 (
(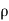 u) +
u) +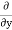 (
(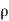 v) +
v) +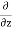 (
(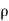 w)] dx dy dz =
w)] dx dy dz = 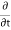 (
(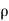 dx dy dz)
dx dy dz)
Simplification and rearrangement of teams would reduce the above expression to
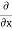 (
(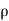 u) +
u) + 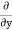 (
(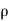 v) +
v) + 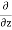 (
(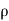 w) +
w) + 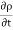 =0
=0
This eq. is the general equation of continuity in three dimension and is applicable to any type of flow and for any fluid whether compressible as incompressible
For steady flow (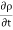 =0) incompressible fluids (
=0) incompressible fluids (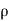 = constant) the equation reduces to
= constant) the equation reduces to
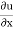 +
+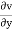 +
+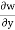 =0
=0
For two-dimensional flow eq. reduce to
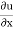 +
+ 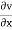 =0
=0
Q6) Derive the Equation of continuity for one-dimensional flow along a streamline.
A6) The continuity equation is based on the principle of conservation of mass. It states as follows
If no fluid is added or removed from the pipe in any length then the mass passing across different sections shall be same.
Consider two cross-sections of a pipe as shown in fig.
Let, A1&A2 = Areas of the pipe at section 1-1 & section 2-2 respectively.
V1 & V2 = Velocities of the fluid at section 1-1 & section 2-2 respectively.
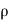 1 &
1 &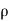 2 = Densities of the fluid at section 1-1 & section 2-2 respectively.
2 = Densities of the fluid at section 1-1 & section 2-2 respectively.
Total quantity of fluid passing through the section 1-1 = 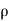 1A1V1
1A1V1
Total quantity of fluid passing through the section 2-2 = 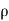 2A2V2
2A2V2
From the law of conservation of matter
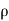 1 A1 V1 =
1 A1 V1 = 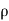 2 A2 V2
2 A2 V2
In case of incompressible fluids 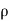 1 =
1 =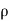 2
2
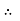 A1 V1 = A2 V2
A1 V1 = A2 V2
Q7) Explain the Types of motion – Rotational & Irrotational motion.
A7) Circulation
Circulation (Г) is defined mathematically as the line integral of the tangential velocity about a closed path (center).
Г = 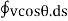
v = velocity in the flow field at the element ds and
ϴ = angle between v and tangent to the path (in the positive anticlockwise direction along the path) at that point.
Vorticity
The vorticity (Ω) is defined as the circulation per unit of enclosed are
Ω = 
If a flow possesses vorticity, it is rotational.
Rotation 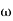 is defined as one half of the vorticity.
is defined as one half of the vorticity.
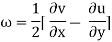
The flow is irrational if rotation 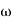 is zero.
is zero.
For three-dimensional flow
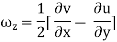
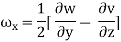
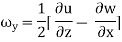
In the vector notation, the above equation can be written as
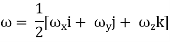
= (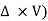
The vector (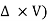 is the curl of velocity vector.
is the curl of velocity vector.
Vorticity Ω = Curl V = (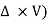
Which may be expressed as
Ω= (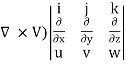
= 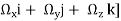
The vorticity components are separately given by
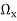 = 2
= 2
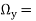 2
2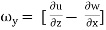
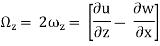
The motion is described as irrotational when the component of rotation or vorticity are zero throughout certain portion of the fluid.
Q8) Define Velocity potential function and stream function.
A8) Potential Function
The velocity potential is defined as scaler function of space and time such that its negative derivative with respect to any directions gives the fluid velocity in that direction.
It is denoted by Ø (phi)
Thus, mathematically the velocity potential is defined as
Ø = f (x, y, z, t)
And Ø = f (x, y, z)
u = -
v = -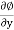
w = -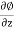
Where u, v and w are the components of velocity in the x, y and z directions respectively.
The negative sign signifies that Ø decreases with an increase in the values of x, y and z. in other words, it indicates that the flow is always in the direction of decreasing Ø.
Stream function –
It is defined as the scalar function of space and time such that its partial derivative with respect to any direction gives the velocity component at right angles to that direction.
It is denoted by Ψ (psi) and defined only for two-dimensional flow.
Mathematically, for ready flow it is defined as Ψ = f(x, y) such that
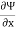 = v
= v
And 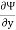 = -u
= -u
Q9) Explain the velocity and acceleration with the help of formula.
A9) Velocity and Acceleration
Let V is the resultant velocity at any point in a fluid flow.
Let u, v and w are its components in x, y and z directions.
The velocity components are functions of space coordinates and time. Mathematically, the velocity components are given as
u = f1(x, y, z, t)
v = f2(x, y, z, t)
w = f3(x, y, z, t)
and Resultant velocity, v = 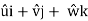
→ |v| = 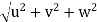
Let ax, ay and az are the total acceleration in x, y and z direction respectively. Then by the chain rule of differentiation, we have
ax = 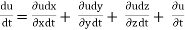
but 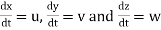
ax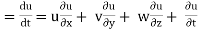
similarly, ay 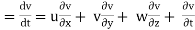
az 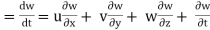
Acceleration vector a = axi + ayj + azk
= 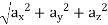
Q10) Define local acceleration and connective acceleration.
A10) Local acceleration is defined as the rate of increase of velocity with respect to time at a given point in a flow field.
The expression 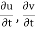 and
and 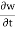 is known as local acceleration.
is known as local acceleration.
Connective acceleration is defined as the rate of change of velocity due to the change of position of fluid particle in a fluid flow. The expression other than 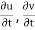 and
and 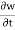 in equation are known as connective acceleration.
in equation are known as connective acceleration.
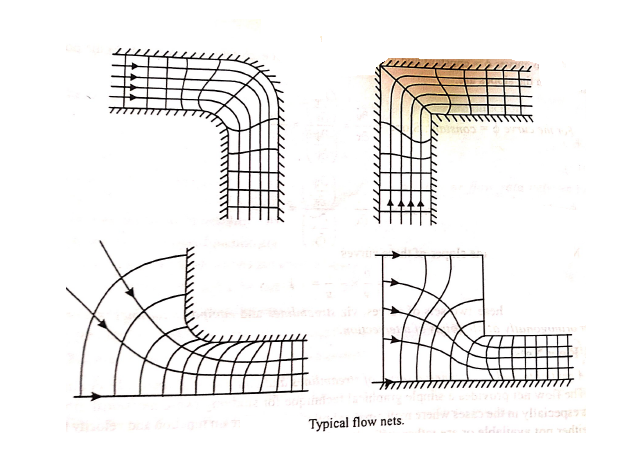
Q11) Define Flow nets. Explain all methods of drawing flow nets.
A11) Flow nets
A grid obtained by drawing a series of streamlines and equipotential lines is known as flow net.
The flow net provides a simple graphical technique for studying two-dimensional irrotational flow especially in the cases where mathematical relation for stream function and velocity function are either not available or are rather difficult and cumbersome to solve.
Methods of drawing flow nets
Analytical method
Here, the equations corresponding to the curves 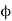 and
and 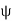 are first obtained and the same are plotted to give the flow net pattern for the flow of fluid between the given boundary shape.
are first obtained and the same are plotted to give the flow net pattern for the flow of fluid between the given boundary shape.
This method can be applied to problem with simple and ideal boundary conditions
Graphical method
A graphical method consists of drawing streamlines and equipotential lines such that they cut orthogonally and form curvilinear squares.
This method consumes lot of time and requires lot of erasing to get the proper shape of a flow net.
Electrical Analogy Method
This method is a practical method of drawing a flow net or a particular set of boundaries.
It is based on the fact that the flow of fluids and flow of electricity through a conductor are analogous.
These two systems are similar in the respect that electric potential is analogous to the velocity potential, electric current is analogous to the velocity of flow and the homogenous conductor is analogous to the homogenous fluid.
Hydraulic Models
Streamlines can be traced by injecting a dye in a seepage model or Heleshaw apparatus.
Then by drawing equipotential lines, the flow net is completed.
Q12) State the uses and limitation of flow nets.
A12) Use of flow nets
Limitations of flow nets
1) The flow net analysis cannot be applied on the region close to the boundary the effects of viscosity are predominant.
2) In case of a flow of a fluid past a solid body, while the flow net gives fairly accurate picture of the flow pattern for the upstream part of solid body, it can give little information concerning the flow conditions at the rare because of separation & eddies.
Q13) Does the following velocity component represent physically possible flow?
u = x2y; v = 2zy – xy2; w = x2 – z2y
A13)
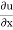 = 2xy
= 2xy
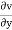 = 2z – 2xy
= 2z – 2xy
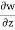 = -2yz
= -2yz
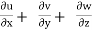 = 2xy + 2z – 2xy – 2yz
= 2xy + 2z – 2xy – 2yz
= 2z – 2yz
≠ 0
Since the continuity equation is not satisfied.
Flow is not physically possible.
Q14) The following represents following velocity components. Calculate the unknown velocity component so that they satisfy the continuity equations.
u = 2x2; v = 2xyz
A14)
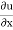 = 4x
= 4x
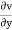 = 2xz
= 2xz
For continuity equation to be satisfied
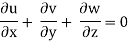
4x + 2xz + 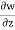 = 0
= 0
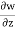 = -4x – 2xz
= -4x – 2xz
 w = (-4x-2xz)
w = (-4x-2xz) z
z
Integrating
w = -4xz - 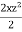
w = -4xz – xz2
Q15) The velocity potential function is given by Ø = 5 (x2 – y2). Calculate velocity components at the point (4,5)
A15)
Ø = 5(x2 – y2)
= 5x2 – 5y2
u = 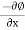
= -10x
v = 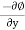
= -(-10y) = 10y
The velocity components at the point (4,5)
u = -10(4)
= -40 units
v = 10(5)
= 50 units
Q16) A stream function is given by Ψ = 5x – 6y. Calculate the velocity components & also magnitude & direction of the resultant velocity.
A16)
Ψ = 5x – 6y
u = 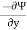
= -(-6)
= 6 units
v = 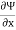
= 5 units
ϴ = 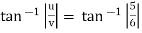
= 39.80˚
Q17) The velocity components in a two-dimensional flow field for an incompressible fluid are as follows.
u = 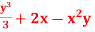 & v = xy2 – 2y -
& v = xy2 – 2y - 
Obtain an expression for the stream function.
A17)
u = 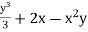
v = xy2 – 2y - 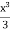
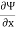 = v
= v
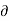 Ψ = (xy2- 2y -
Ψ = (xy2- 2y - 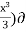 x
x
Integrating w. r. t. x
Ψ = 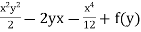 -------------(1)
-------------(1)
Diff w. r. t. y
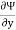 = x2y – 2x + f’(y)
= x2y – 2x + f’(y)
But 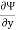 = -u
= -u
-u = x2y – 2x + f’(y)
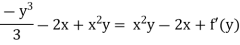
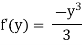
Integrating w.r.to y
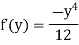
Put in equation (1)
Ψ = 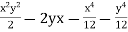
Q18) If for a two-dimensional potential flow, the velocity is given by Ø = x(2y - 1) determine the stream function at point (4,5)
A18)
Ø = x(2y - 1)
= 2xy – x
u = 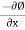
= -(2y - 1)
= -2y + 1
v = 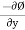
= -(2x)
= -2x
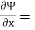 v
v
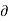 Ψ = -2x
Ψ = -2x 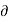 x
x
Integrate w.r.to x
Ψ = 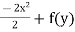
Ψ = -x2 + f(y) --------------------(1)
Diff w.r.to y
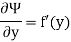
But 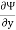 = - u
= - u
-u = f’(y)
2y – 1 = f’(y)
Integrate w.r.to y
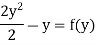
y2 – y = f(y)
put in equation (1)
Ψ = -x2 + y2 – y
Stream function Ψ at (4,5)
Ψ = -42 + 52 – 5
= 4 units
Q19) The stream lines represented by Ψ = x2 + y2. Find its corresponding velocity potential. Determine the velocity and its direction at (2,2).
A19)
Ψ = x2 + y2
u = 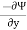
= -2y
v = 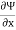
= 2x
At point (2,2)
u = -2(2)
= -4 units
v = 2(2)
= 4 units
V = 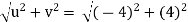
= 5.657 units
ϴ = 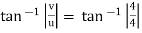
= 45˚
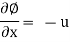
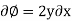
Integrate w.r.to x
Ø = 2yx + f(y) -----------------(1)
Differentiate w.r.to y
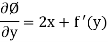
But 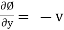
-v = 2x + f’(y)
-2x = 2x + f’(y)
-4x = f’(y)
Integrate w.r.to y
-4xy = f(y)
Put in equation (1)
Ø = 2yx – 4xy
Ø = -2xy
Q20) A flow field is given by v = (x2y) i + (y2z) j – (2xyz + yz2) k. prove that it is a case of possible steady incompressible fluid flow. Calculate velocity & acceleration at the point (2,1,3)
A20) u = x2y = (22× 1) = 4 units
v = y2z = (12× 3) = 3 units
w = -2xyz – yz2 = -2 × 2 × 1 × 3 – 1 × 32 = -21 units
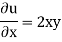
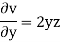
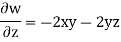
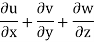
= 2xy + 2yz – 2xy – 2yz
= 0
Hence it is satisfying continuity equation
It is possible case of fluid flow
v = 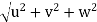
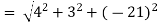
= 21.587 units
ax = 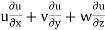
= 4 × 2xy + 3 × x2 – 21 × 0
= 4 × 2 × 2 × 1 + 3 × 22
= 28 units
ay = 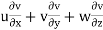
= 4 × 0 + 3 × 2yz – 21 × y2
= 3 × 2 × 1 × 3 – 21 × 22
= - 3 units
az = 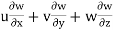
= 4 × -2yz + 3 × (-2xz – z2) – 21(-2xy – 2yz)
= 4 × -2 × 1 × 3 + 3(-2 × 2 × 3 - 32) – 21(-2 × 2 × 1 – 2 × 1 × 3)
= 123 units
a = 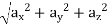
= 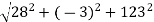
= 126.18 units