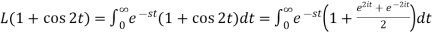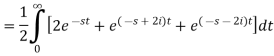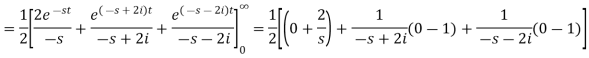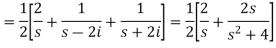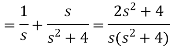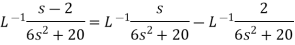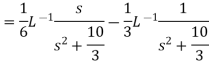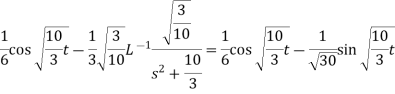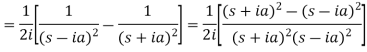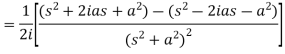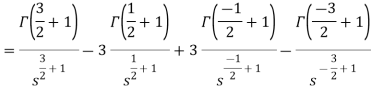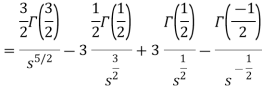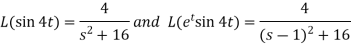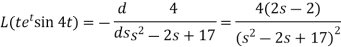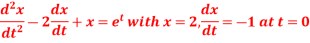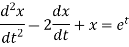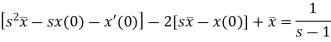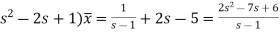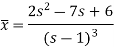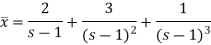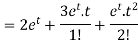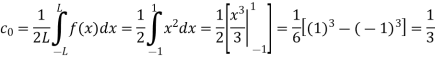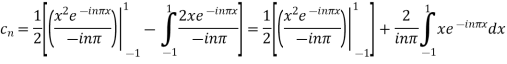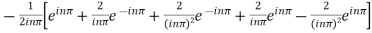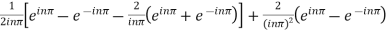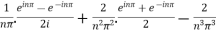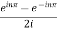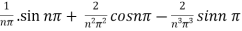Math
Unit-2TransformsQuestion-1: Find the Laplace transform of the following functions-1. 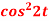 2.
2. 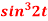 Sol. 1. Here
Sol. 1. Here 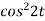 So that we can write it as-
So that we can write it as-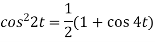 Now-
Now-
2. Since  Or
Or  Now-
Now-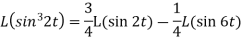
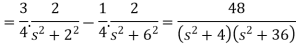 Question-2: Find the Laplace transform of (1 + cos 2t)
Question-2: Find the Laplace transform of (1 + cos 2t)
So that-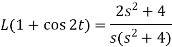 Question-3: Find the inverse Laplace transform of-
Question-3: Find the inverse Laplace transform of-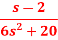 Sol.
Sol.
Question-4: Find the inverse Laplace transform of-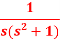 Sol.
Sol.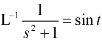

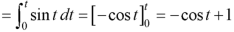 Question-5: Find the inverse transform of-
Question-5: Find the inverse transform of-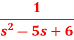 Sol.First we will convert it into partial fractions-
Sol.First we will convert it into partial fractions-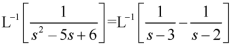
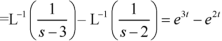 Qustion-6: Find the Laplace transform of t sin at.Sol. Here-
Qustion-6: Find the Laplace transform of t sin at.Sol. Here-
Question-7: Find the Laplace transform of 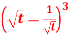 Sol. Here-
Sol. Here-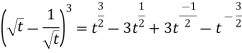 So that-
So that-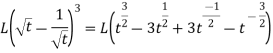
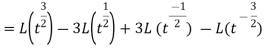
As we know that- 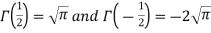 So that-
So that-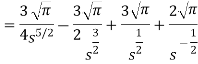
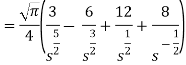 Hence-
Hence- Question-8: Find the Laplace transform of
Question-8: Find the Laplace transform of  .Sol. Here-
.Sol. Here-
Now-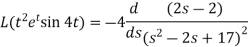
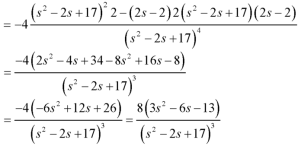 Question-9: Use Laplace transform method to solve the following equation-
Question-9: Use Laplace transform method to solve the following equation-
Question-10: Using complex form find the Fourier series of the function f(x) = x2, defined on te interval [-1,1]Solution:Here the half-period is L=1.Therefore, the co-efficient c0 is,
For n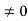
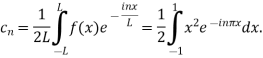 Integrating by parts twice,we obtain
Integrating by parts twice,we obtain
Question-11: Find the Fourier transform of 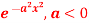 Sol. As we know that the Fourier transform of f(x) will be-
Sol. As we know that the Fourier transform of f(x) will be- So that-
So that-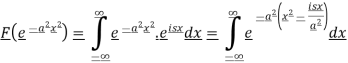
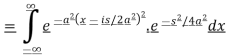 Now put
Now put 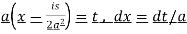
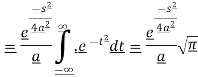 So that-
So that-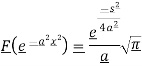 Question-12: Find the Fourier sine transform of
Question-12: Find the Fourier sine transform of 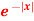 Sol. Here x being positive in the interval (0, ∞)
Sol. Here x being positive in the interval (0, ∞) 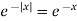 Fourier sine transform of
Fourier sine transform of 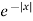 will be-
will be-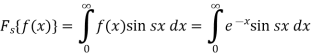
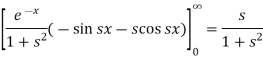
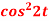 2.
2. 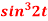 Sol. 1. Here
Sol. 1. Here 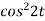 So that we can write it as-
So that we can write it as-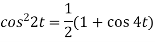 Now-
Now-
|
 Or
Or  Now-
Now-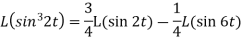
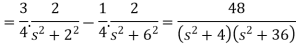 Question-2: Find the Laplace transform of (1 + cos 2t)
Question-2: Find the Laplace transform of (1 + cos 2t)Sol.
|
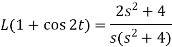 Question-3: Find the inverse Laplace transform of-
Question-3: Find the inverse Laplace transform of-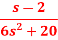 Sol.
Sol.
|
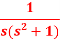 Sol.
Sol.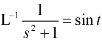

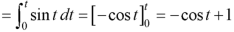 Question-5: Find the inverse transform of-
Question-5: Find the inverse transform of-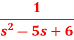 Sol.First we will convert it into partial fractions-
Sol.First we will convert it into partial fractions-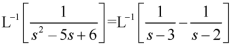
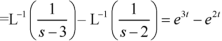 Qustion-6: Find the Laplace transform of t sin at.Sol. Here-
Qustion-6: Find the Laplace transform of t sin at.Sol. Here-
|
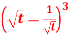 Sol. Here-
Sol. Here-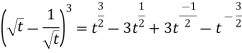 So that-
So that-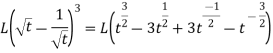
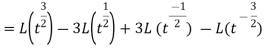
|
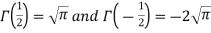 So that-
So that-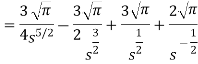
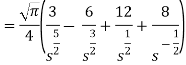 Hence-
Hence- Question-8: Find the Laplace transform of
Question-8: Find the Laplace transform of  .Sol. Here-
.Sol. Here-
|
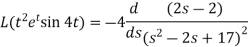
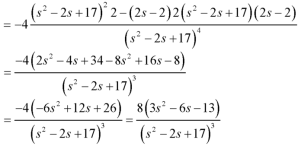 Question-9: Use Laplace transform method to solve the following equation-
Question-9: Use Laplace transform method to solve the following equation-
|
Sol. Here we have-
Take Laplace transform of both sides, we get-
It becomes- ( So that-
Now breaking it into partial fractions-
We get the following results on inversion-
|
|
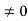
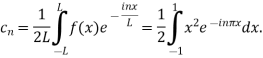 Integrating by parts twice,we obtain
Integrating by parts twice,we obtain
=
=
=
= |
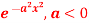 Sol. As we know that the Fourier transform of f(x) will be-
Sol. As we know that the Fourier transform of f(x) will be- So that-
So that-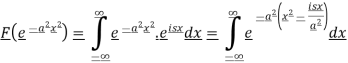
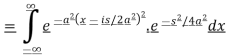 Now put
Now put 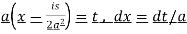
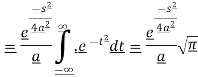 So that-
So that-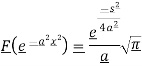 Question-12: Find the Fourier sine transform of
Question-12: Find the Fourier sine transform of 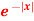 Sol. Here x being positive in the interval (0, ∞)
Sol. Here x being positive in the interval (0, ∞) 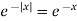 Fourier sine transform of
Fourier sine transform of 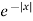 will be-
will be-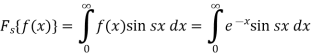
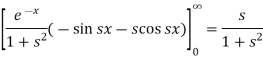
0 matching results found