Unit - 2

Data Acquisition and Signal Communication

Q1) A modulating signal m(t)=10cos(2π×103t) is amplitude modulated with a carrier signal c(t)=50cos(2π×105t). Find the modulation index, the carrier power, and the power required for transmitting AM wave.

A1) Given, the equation of modulating signal as

m(t)=10cos(2π×103t)

We know the standard equation of modulating signal as

m(t)=Amcos(2πfmt)

Comparing both equations, we get

Amplitude of modulating signal as Am=10volts

And Frequency of modulating signal as fm=103Hz=1KHz

c(t)=50cos(2π×105t)

Comparing these two equations, we will get

Amplitude of carrier signal as Ac=50volts

And Frequency of carrier signal as fc=105Hz=100KHz

μ = Am/Ac

μ = 10/50 =0.2

The value of modulation index is 0.2

Carrier power, Pc

Pc=Ac2/2R

Let R=1ohm

Carrier power, Pc is 1250 watts.

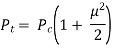
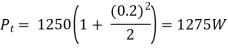
Q2) The equation of amplitude wave is given by s(t)=20[1+0.8cos(2π×103t)] cos(4π×105t). Find the carrier power, the total sideband power, and the band width of AM wave.

A2) s(t)=20[1+0.8cos(2π×103t)] cos(4π×105t).

We can write above equation as

s(t)=20[1+0.8cos(2π×103t)] cos (4πx 2 x105t).

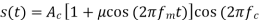t)

Amplitude of carrier signal as Ac=20volts

Modulation index as μ=0.8

Frequency of modulating signal as fm=103Hz=1KHz

Frequency of carrier signal as fc=2×105Hz=200KHz

The formula for Carrier power, Pc

Pc=Ac2/2R

Pc = (20)2/2(1) = 200W

Total side band power is

PSB=Pcμ2/2

PSB=200×(0.8)2/2=64W

Total side band power is 64 watts.

We know the formula for bandwidth of AM wave is

BW=2fm

Substitute fm value in the above formula.

BW=2(1K) =2KHz

The bandwidth of AM wave is 2 KHz.

Q3) A carrier is phase modulated (PM) with frequency deviation of 10 kHz by a single tone frequency of 1 kHz. If the single tone frequency is increased to 2 kHz, assuming that phase deviation remains unchanged the bandwidth of the PM signal is

A3)

• In PM phase deviation,
• 
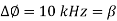
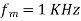
• If the frequency 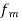is increased to 2 kHz and phase deviation remains unchanged
• The modulation index
• 
• According to carsons rule
• Bandwidth=

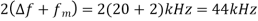
Q4) A device with input 𝑥(𝑡) and output 𝑦(𝑡) is characterized by: 𝑦(𝑡)=𝑥2 (𝑡). An FM signal with frequency deviation of 90 KHz and modulating signal bandwidth of 5 KHz is applied to this device. The bandwidth of the output signal is (a) 370 KHz (b) 190 KHz (c) 380 KHz (d) 95 KHz

A4) Frequency deviation Δ𝒇=𝟗𝟎𝑲𝑯𝒛

Modulating signal bandwidth = 5 KMz

When FM signal is applied to doubler frequency deviation doubles.

𝑩.𝑾 = 𝟐(Δ𝒇+𝒇𝒎) = 𝟐(𝟏𝟖𝟎+𝟓) =𝟑𝟕𝟎 𝑲𝑯z

Q5) An FM signal with a modulation index 9 is applied to a frequency tripler. The modulation index in the output signal will be (a) 0 (b) 3 (c) 9 (d) 27

A5) The frequency modulation index β is multiplied by n in n-times frequency multiplier.

𝑺𝒐, 𝜷′=𝟑×𝟗 = 27

Q6) A sinusoidal modulating waveform of amplitude 5 V and a frequency of 2 KHz is applied to FM generator, which has a frequency sensitivity of 40 Hz/volt. Calculate the frequency deviation, modulation index, and bandwidth.

A6) Given, the amplitude of modulating signal, Am=5V

Frequency of modulating signal, fm=2KHz

Frequency sensitivity, kf=40Hz/volt

We know the formula for Frequency deviation as

Δf=kfAm

­­Δf=40×5=200Hz

β=Δf/fm

β=200/(2×1000) = 0.1

The formula for Bandwidth of Narrow Band FM is the same as that of AM wave.

BW=2fm

BW=2×2K=4KHz

Q7) An FM wave is given by s(t)=20cos(8π×106t+9sin(2π×103t)). Calculate the frequency deviation, bandwidth, and power of FM wave.

A7) s(t)=20cos(8π×106t+9sin(2π×103t))

We know the standard equation of an FM wave as

s(t)=Accos(2πfct+βsin(2πfmt))

Amplitude of the carrier signal, Ac=20V

Frequency of the carrier signal, fc=4×106Hz=4MHz

Frequency of the message signal, fm=1×103Hz=1KHz

Modulation index, β=9

β=Δf/fm

Δf=9×1K=9KHz

The formula for Bandwidth of Wide Band FM wave is

BW=2(β+1)fm

BW=2(9+1)1K=20KHz

The bandwidth of Wide Band FM wave is 20KHz

Pc=Ac2/2R

P= (20)2/2(1) =200W

Therefore, the power of FM wave is 200watts.

Q8) In a summing amplifier, if R = 1kΩ, Va = +3V, Vb = +8V, Vc = +9V, Vd = +5V and supply voltage is ±15V. Find the output voltage Vo.

A8) Vo = Sum of all input voltages applied at both the terminals

Vo = Va + Vb + Vc +Vd

Vo = -3 -8 +9 +5

Vo = +3V

Q9) Find the output voltage for the given circuit diagram if Rf = 5kΩ.

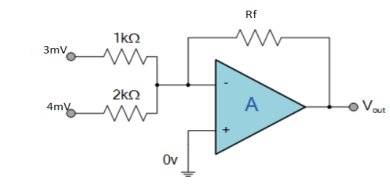
A9)

We know,

Gain (Av) = =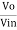

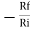
Hence,

Av1 =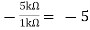

Av2 =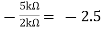

Now, Output voltage Vo = Sum of the two amplified input signals

Vo = Av1 x V1 + Av2 x V2

Vo =(-5 x 3) + ( -2.5x 4) mV

Vo = -25mV

As the above output voltage is negative hence it is an inverting amplifier.

Q10) A 200mV peak to peak sine waveform voltage is applied to Op-amp inverting amplifier with Rf/R1 = 10.

A10) Peak to peak input voltage

2Vm = 200 mV

Vm = 100 mV

Vi= Vm sin wt = 100 sin wt mV

Vo = -Rf/R1 x vi = -10 x 100 sinwt mV

= -1000 sin wt mV

Q11) Design a non-inverting amplifier using Op-amp with a closed loop voltage gain of 10.

A11)

Af = 1 + Rf/R1 =10

Rf/R1 = 9

Rf = 9 R1

If R1 = 1K

Rf = 9K Ω

Q12) In an op-amp inverting amplifier R1 = 1K Ω and Rf = 100KΩ. The DC supply voltage of the op-amp is ± 15V. Calculate the output voltage if input voltage is 1V.

A12)

R1 = 1KΩ Rf = 100KΩ

V+ = 15V and V-=-15V. Vi = 1V

Af = -Rf/R1 = -100K/1K = -100

Af = vo/vi

Vo = Af vi

= -100 x 1V = -100V

The output voltage cannot exceed the DC power supply voltage. Since vo is negative and large it is limited to V-

Vo ≈ V- = -15V

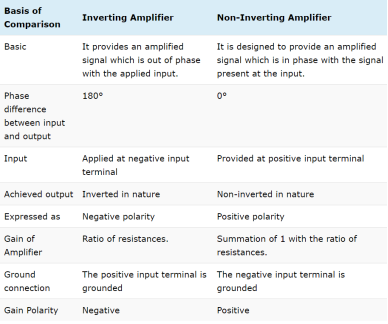
Q13) Compare inverting, non-inverting and differential amplifier?

A13)

Q14) Explain synchronous and asynchronous types of communications?

A14) Types of Communication system

1)Synchronous transmission

In synchronous transmission, data moves in a completely paired approach, in the form of chunks or frames.  Synchronisation between the source and target is required so that the source knows where the new byte begins, since there are no spaces included between the data. Synchronous transmission is effective, dependable, and often utilised for transmitting a large amount of data.  It offers real-time communication between linked devices.An example of synchronous transmission would be the transfer of a large text file.  Before the file is transmitted, it is first dissected into blocks of sentences.  The blocks are then transferred over the communication link to the target location.

Characteristics of Synchronous Transmission

• There are no spaces in between characters being sent.
• Timing is provided by modems or other devices at the end of the transmission.
• Special ’syn’ characters go before the data being sent.
• The syn characters are included between chunks of data for timing functions.

Examples of Synchronous Transmission

• Chatrooms
• Video conferencing
• Telephonic conversations
• Face-to-face interactions

2)Asynchronous Transmission

In asynchronous transmission, data moves in a half-paired approach, 1 byte or 1 character at a time.  It sends the data in a constant current of bytes.  The size of a character transmitted is 8 bits, with a parity bit added both at the beginning and at the end, making it a total of 10 bits.  It doesn’t need a clock for integration—rather, it utilises the parity bits to tell the receiver how to translate the data.It is straightforward, quick, cost-effective, and doesn’t need 2-way communication to function.

Characteristics of Asynchronous Transmission

• Each character is headed by a beginning bit and concluded with one or more end bits.
• There may be gaps or spaces in between characters.

Examples of Asynchronous Transmission

• Emails
• Forums
• Letters
• Radios
• Televisions

Q15) Write short notes on programmable control amplifier?

A15) Programmable gain amplifiers are typically non-inverting operational amplifiers with a digitally controlled analog switch connected to several resistors in its feedback loop. An external computer or another logic or binary signal controls the addressable inputs of the analog switch so it selects a certain resistor for particular gain. The data acquisition system’s signal conditioners sense the input signal amplitude and automatically send the proper binary code to the programmable gain amplifier (PGA) to increase the gain for a low signal, or decrease the gain for a large signal. The input signal then can be measured and displayed without distortion.

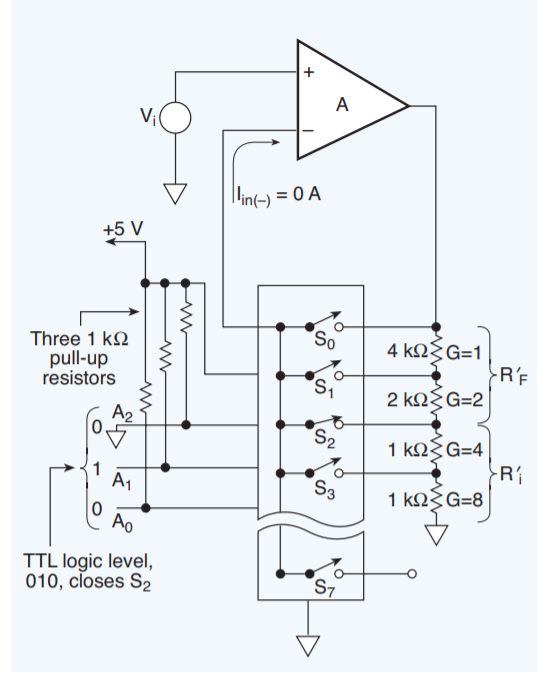
Fig: Programmable gain Amplifier

Q16) Explain instrumentation amplifier with circuit diagram?

A16) The Instrumentation amplifiers consist of three op-amps. In this circuit, a non-inverting amplifier is connected to each input of the differential amplifier.

This instrumentation amplifier provides high input impedance for exact measurement of input data from transducers. The circuit diagram of an instrumentation amplifier is as shown in the figure below.

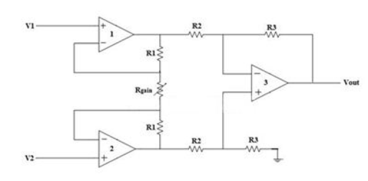
Fig: Instrumentation Amplifier

The op-amps 1 & 2 are non-inverting amplifiers and together form an input stage of the instrumentation amplifier. The op-amp 3 is a difference amplifier that forms the output stage of the instrumentation amplifier.

Working

The output stage of the instrumentation amplifier is a difference amplifier, whose output Vout is the amplified difference of the input signals applied to its input terminals.

If the outputs of op-amp 1 and op-amp 2 are Vo1 and Vo2 respectively, then the output of the difference amplifier is given by,

Vout = (R3/R2)(Vo1-Vo2)

The expressions for Vo1 and Vo2 can be found in terms of the input voltages and resistances.

Consider the input stage of the instrumentation amplifier as shown in the figure below.

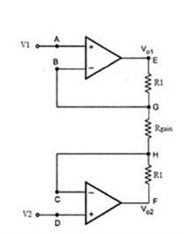
Fig: Input Stage of Instrumentation Amplifier

The potential at node A is the input voltage V1. Hence the potential at node B is also V1, from the virtual short concept. Thus, the potential at node G is also V1.

The potential at node D is the input voltage V2. Hence the potential at node C is also V2, from the virtual short. Thus, the potential at node H is also V2.

Ideally the current to the input stage op-amps is zero. Therefore, the current I through the resistors R1, Rgain and R1 remains the same.

Applying Ohm’s law between the nodes E and F,

I = (Vo1-Vo2)/(R1+Rgain+R1) ——————— 1

I = (Vo1-Vo2)/(2R1+Rgain)

Since no current is flowing to the input of the op-amps 1 & 2, the current I between the nodes G and H can be given as,

I = (VG-VH)/Rgain = (V1-V2)/Rgain ————————- 2

Equating equations 1 and 2,

(Vo1-Vo2)/(2R1+Rgain) = (V1-V2)/Rgain 

(Vo1-Vo2) = (2R1+Rgain) (V1-V2)/Rgain —————— 3

The output of the difference amplifier is given as,

Vout = (R3/R2) (Vo1-Vo2)

Therefore, (Vo1 – Vo2) = (R2/R3)Vout

Substituting (Vo1 – Vo2) value in the equation 3, we get

(R2/R3)Vout = (2R1+Rgain)(V1-V2)/Rgain

i.e. Vout = (R3/R2) {(2R1+Rgain)/Rgain} (V1-V2)

The above equation gives the output voltage of an instrumentation amplifier. The overall gain of the amplifier is given by the term (R3/R2) {(2R1+Rgain)/Rgain}.

Q17) Compare inverting and non inverting amplifier?

A17)

Q18) Write short notes on quantization?

A18) Quantizing is defined as the transformation of a continuous analog input into a set of discrete output states. Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC). It is a rounding error between the analog input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent.

An analog-to-digital converter is an electronic device that converts an analog voltage to a digital code. The output of the A/D converter can be directly interfaced to digital devices such as microcontrollers and computers. The resolution of an A/D converter is the number of bits used to digitally approximate the analog value of the input. The number of possible states N is equal to the number of bit combinations that can be output from the converter:

N=2n

Where n is the number of bits. For the example illustrated in Figure, the 3-bit device has 23 or 8 output states as listed in the first column. The output states are

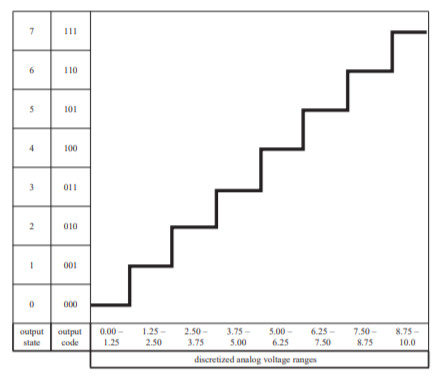
Fig: A/D conversion

Usually numbered consecutively from 0 to (N- 1). The corresponding code word for each output state is listed in the second column. Most commercial A/D converters are 8-, 10-, or 12-bit devices that resolve 256, 1024, and 4096 output states, respectively. The number of analog decision points that occur in the process of quantizing is (N- 1). In Figure above, the decision points occur at 1.25 V, 2.50 V, . . . , and 8.75 V. The analog quantization size Q, sometimes called the code width, is defined as the full-scale range of the A/D converter divided by the number of output states

Q=(Vmax-Vmin)/N

It is a measure of the analog change that can be resolved by the converter. Although the term resolution is defined as the number of output bits from an A/D converter, sometimes it is used to refer to the analog quantization size. For our example, the analog quantization size is 10/8 V 1.25 V. This means that the amplitude of the digitized signal has an error of at most 1.25 V. Therefore, the A/D converter can only resolve a voltage to within 1.25 V of the exact analog voltage.

Q19) List difference between AM/FM?

A19)