Unit - 1
Roots of Equation and Simultaneous Equations
Q1) Explain bisection method.
A1)
Bisection method consists of finding the root of the equation 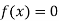 which lies between a and b (say).
which lies between a and b (say).
The function  is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
is continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is
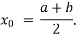
If , then the correct root is
, then the correct root is 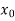 .But if
.But if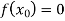 , then the root either lies between a and
, then the root either lies between a and 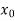 or
or 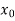 and b according as
and b according as 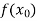 is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
is positive or negative, we again bisect the interval as above and the process is repeated the root is found to desired accuracy.
Q2) Find a real root of 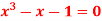 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
A2)
Let  then by hit and trial we have
then by hit and trial we have
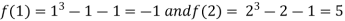
Thus  .So the root of the given equation should lies between 1 and 2.
.So the root of the given equation should lies between 1 and 2.

Now, 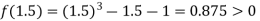
I.e. positive so the root of the given equation must lies between 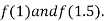

Now, 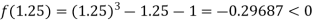
i.e., negative so the root of the given equation lies between 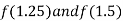
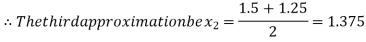
Now, 
i.e., positive so the root of the given equation lies between 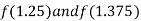
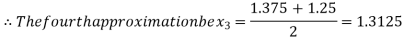
Now, 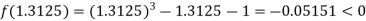
i.e., negative so that the root of the given equation lies between 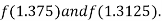
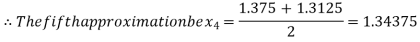
Now, 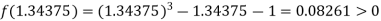
i.e., positive so that the root of the given equation lies between 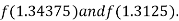
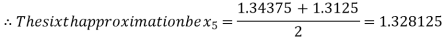
Now, 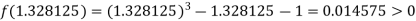
i.e., positive so that the root of the given equation lies between 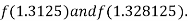
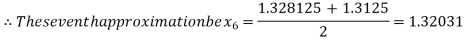
Now, 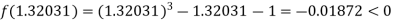
i.e., negative so that the root of the given equation lies between 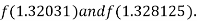
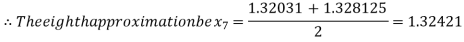
Now, 
i.e., negative so that the root of the given equation lies between 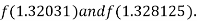
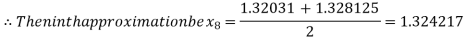
Hence the approximate root of the given equation is 1.32421
Q3) What do you understand by Regula-falsi method?
A3)
This is the oldest method of finding the approximate numerical value of a real root of an equation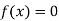 .
.
In this method we suppose that 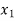 and
and  are two points where
are two points where 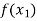 and
and 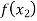 are of opposite sign. Let
are of opposite sign. Let 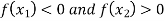
Hence the root of the equation 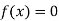 lies between
lies between 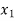 and
and  and so,
and so, 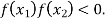
The Regula Falsi formula

Find  is positive or negative. If
is positive or negative. If 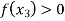 then root lies between
then root lies between 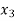 and
and 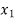 or if
or if 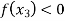 then root lies between
then root lies between 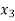 and
and 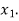 similarly we calculate
similarly we calculate 
Q4) Find the real root of the equation

By the method of false position correct to four decimal places
A4)
Let 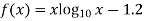
By hit and trail method
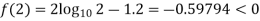
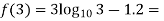 0.23136 > 0
0.23136 > 0
So, the root of the equation 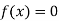 lies between
lies between  2 and
2 and 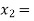 3 and also
3 and also 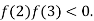
By Regula Falsi Method
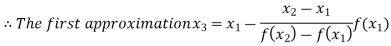
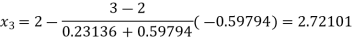
Now, 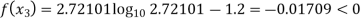
So, root of the equation 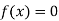 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 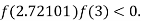
By Regula Falsi Method
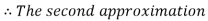
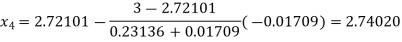
Now, 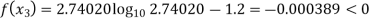
So, root of the equation 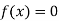 lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 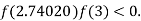
By Regula Falsi Method
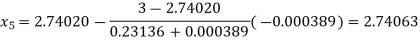
Now, 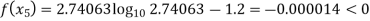
So, root of the equation 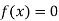 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 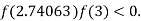
By Regula Falsi Method


Hence the root of the given equation correct to four decimal places is 2.7406
Q5) Apply Regula Falsi Method to solve the equation
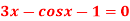
A5)
Let 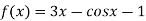
By hit and trail
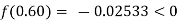
And 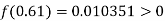
So, the root of the equation lies between 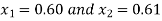 and also
and also 
By Regula Falsi Method
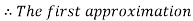
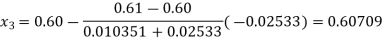
Now, 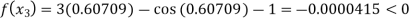
So, root of the equation 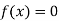 lies between 0.60709 and 0.61 and also
lies between 0.60709 and 0.61 and also 
By Regula Falsi Method
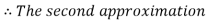

Now, 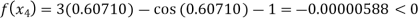
So, root of the equation 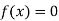 lies between 0.60710 and 0.61 and also
lies between 0.60710 and 0.61 and also 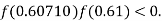
By Regula Falsi Method
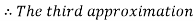
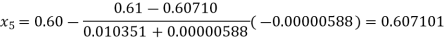
Hence the root of the given equation correct to five decimal place is 0.60710.
Q6) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: .
.
A6)
Given 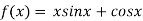
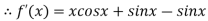
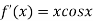
By Newton Raphson Method
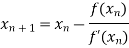
= 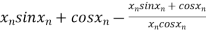
=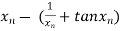
The initial approximation is 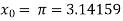 in radian.
in radian.
For n =0, the first approximation 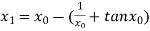
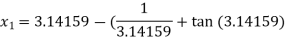
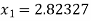
For n =1, the second approximation 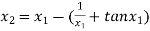

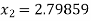
For n =2, the third approximation 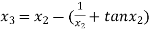
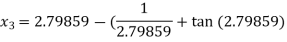
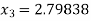
For n =3, the fourth approximation 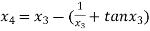
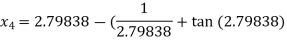
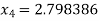
Hence the root of the given equation corrects to five decimal place 2.79838.
Q7) Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 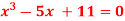
A7)
Let 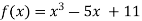
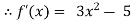
By Newton Raphson Method
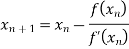
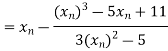

Let the initial approximation be 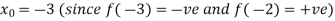
For n=0, the first approximation 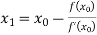
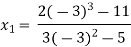
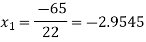
For n=1, the second approximation 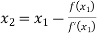
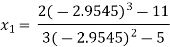
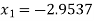
For n=2, the third approximation 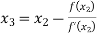
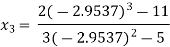
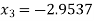
Since 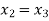 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Q8) Solve the equation by Gauss Elimination Method:

A8)
Given
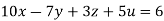
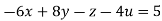
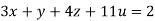
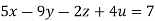
Rewrite the given equation as
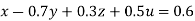 … (i)
… (i)
 ….(ii)
….(ii)
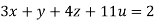 ….(iii)
….(iii)
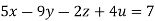 …(iv)
…(iv)
(I) We eliminate x from (ii), (iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
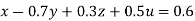 …(i)
…(i)
 ….(v)
….(v)
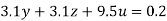 ….(vi)
….(vi)
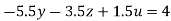 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
 …(i)
…(i)
 ….(v)
….(v)
 …(viii)
…(viii)
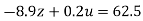 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
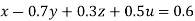 … (i)
… (i)
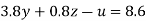 ….(v)
….(v)
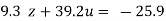 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 
Form eq(v), we get 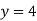
From eq(i), 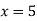
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Q9) Apply Gauss Elimination Method to solve the following system of equation:
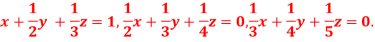
A9)
Given 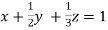 … (i)
… (i)
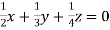 … (ii)
… (ii)
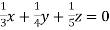 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply 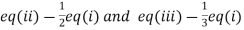 we get
we get
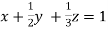 … (i)
… (i)
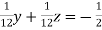 … (iv)
… (iv)
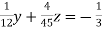 … (v)
… (v)
(II) We eliminate y from (v)
Apply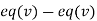 we get
we get
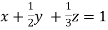 … (i)
… (i)
 … (vi)
… (vi)
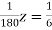 … (vii)
… (vii)
(III) Back substitution
From (vii) 
From (vi) 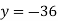
From (i) 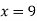
Hence the solution of the equation is 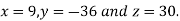
Q10) Use Jacobi’s method to solve the system of equations:
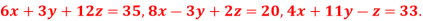
A10)
Since 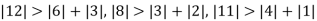
So, we express the unknown with large coefficient in terms of other coefficients.
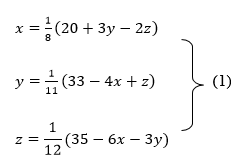
Let the initial approximation be 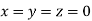
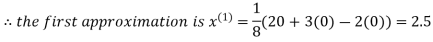
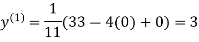
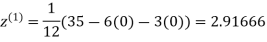

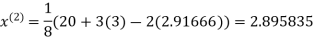
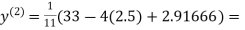 2.35606
2.35606
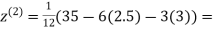 0.91666
0.91666
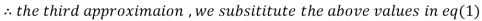
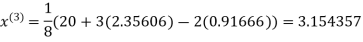


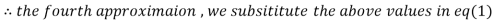
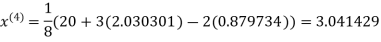
 1.932936
1.932936
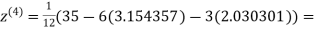 0.831912
0.831912
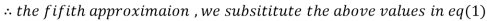
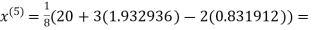 3.016873
3.016873
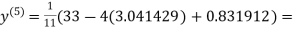 1.969654
1.969654
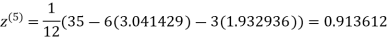
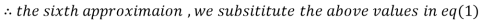
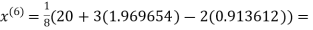 3.010217
3.010217
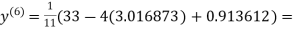 1.986010
1.986010
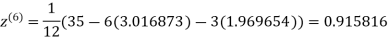
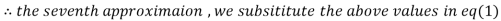
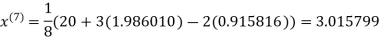
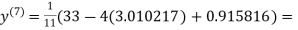 1.988631
1.988631
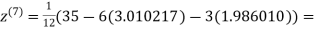 0.915055
0.915055


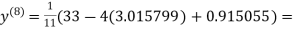 1.986532
1.986532
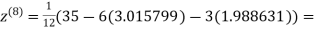 0.911609
0.911609
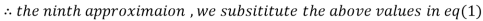
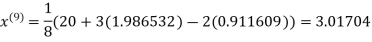
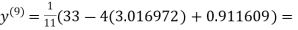 1.985792
1.985792
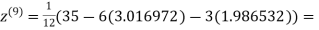 0.911547
0.911547

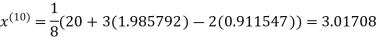
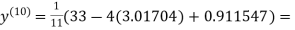 1.98576
1.98576
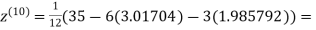 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 
Q11) Use Gauss –Seidel Iteration method to solve the system of equations

A11)
Since 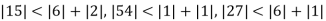
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
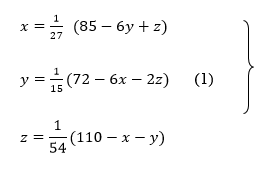
Let the initial approximation be 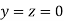
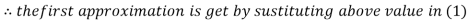
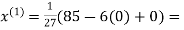 3.14814
3.14814
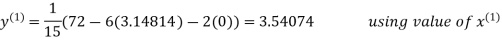
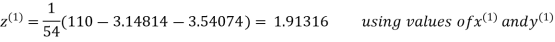
 2.43217
2.43217
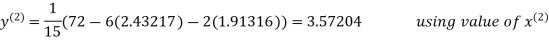
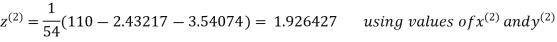
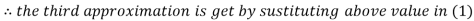
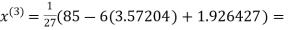 2.42571
2.42571

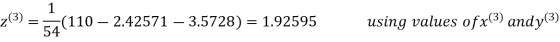
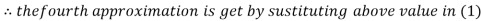
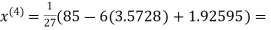 2.4260
2.4260
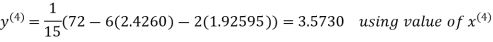
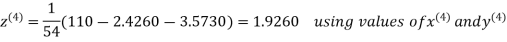
Hence the solution correct to three decimal places is
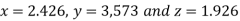
Q12) Solve the following equations by Gauss-Seidel Method
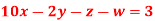
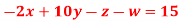
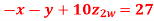
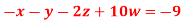
A12)
Rewrite the above system of equations
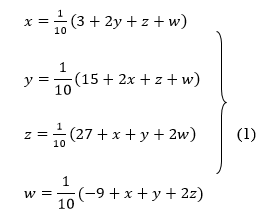
Let the initial approximation be 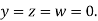

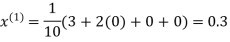
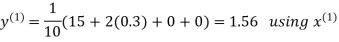

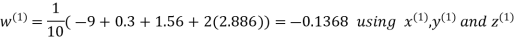

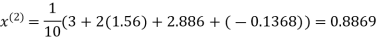
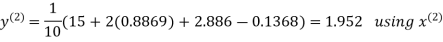
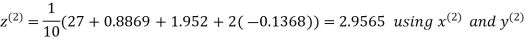
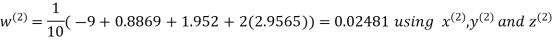

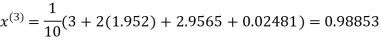
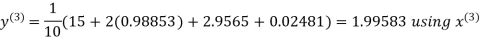
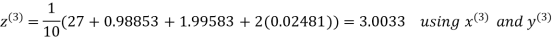
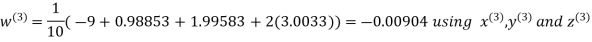


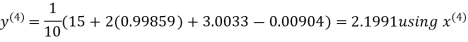

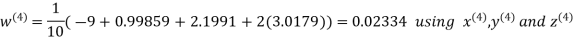

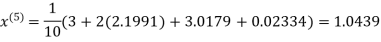
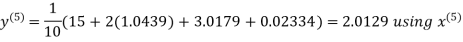
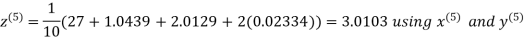
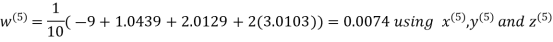
Hence the required solution is 
Q13) Solve the system of equations
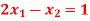
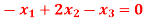
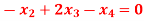

A13)
The given system of equation is a tri-diagonal system
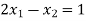 ….(1)
….(1)
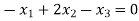 ….(2)
….(2)
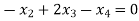 ….(3)
….(3)
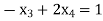 …(4)
…(4)
Here the main diagonal elements are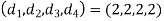 , super diagonal elements
, super diagonal elements 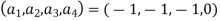 and the sub diagonal elements are
and the sub diagonal elements are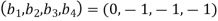 . Also
. Also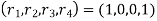 .
.
We know that 
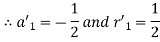
Again, we have 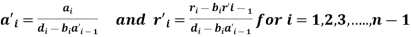
For 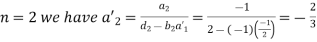
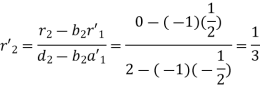
For 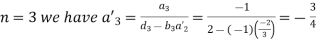
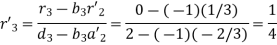
For 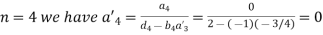
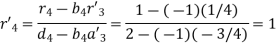
Hence the system will be
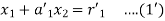
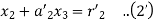
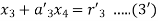
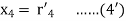
On putting values, we get
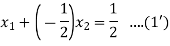
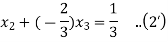
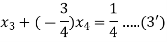
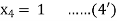
Hence 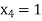
Putting value of 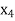 in equation (3’) we get
in equation (3’) we get 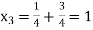
Putting values of 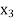 in equation (2’) we get
in equation (2’) we get 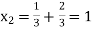
Putting the value of 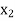 in equation (1’) we get
in equation (1’) we get 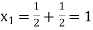
Hence the solution is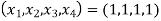 .
.
Q14) Solve the system 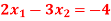
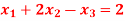
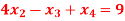
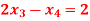
A14)
The given system is a tri-diagonal system
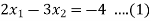
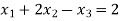 …..(2)
…..(2)
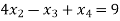 ….(3)
….(3)
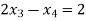 …..(4)
…..(4)
Here the main diagonal elements are 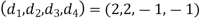 , the super diagonal elements are
, the super diagonal elements are 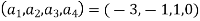 , the sub diagonal elements are
, the sub diagonal elements are 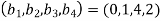 and the right side coefficient are
and the right side coefficient are  .
.
We know that 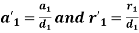
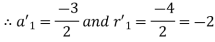
Again, we have 
For 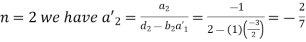

For 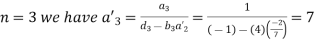
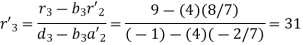
For 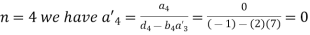
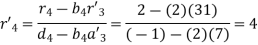
Hence the system will be
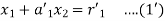

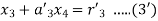
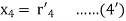
On putting values, we get
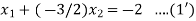
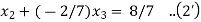
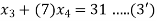
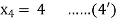
Hence 
Putting value of  in equation (3’) we get
in equation (3’) we get 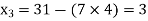
Putting values of 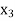 in equation (2’) we get
in equation (2’) we get 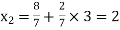
Putting the value of 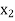 in equation (1’) we get
in equation (1’) we get 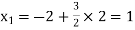
Hence the solution is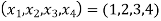 .
.
Q15) Solve the system
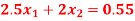

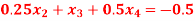
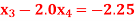
A15)
The given system is a tri-diagonal system

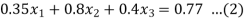
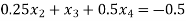 ….(3)
….(3)

Here the main diagonal elements are 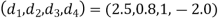 , the super diagonal elements are
, the super diagonal elements are 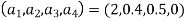 , the sub diagonal elements are
, the sub diagonal elements are 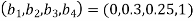 and the right side coefficient are
and the right side coefficient are 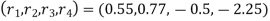 .
.
We know that 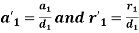

Again, we have 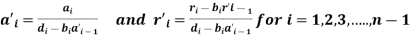
For 
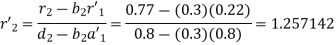
For 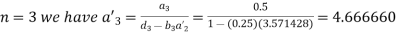
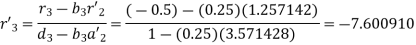
For 
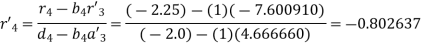
Hence the system will be
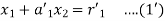
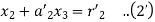
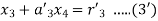
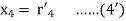
On putting values, we get
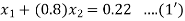
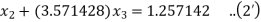
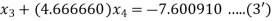

Hence 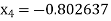
Putting value of 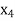 in equation (3’) we get
in equation (3’) we get
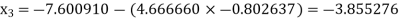
Putting values of  in equation (2’) we get
in equation (2’) we get

Putting the value of  in equation (1’) we get
in equation (1’) we get 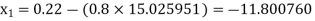
Hence the solution is
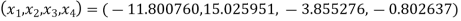 .
.