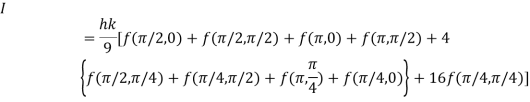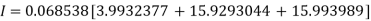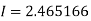Unit - 3
Numerical Integration
Q1) What is trapezoidal rule?
A1)
Let the interval 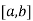 be divided into n equal intervals such that
be divided into n equal intervals such that 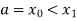 <
<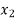 <…. <
<…. <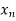 =b.
=b.
Here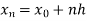 .
.
To find the value of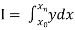 .
.
Setting n=1, we get
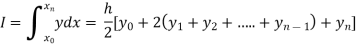
Or I = 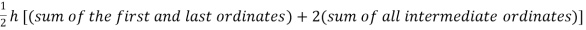
The above is known as Trapezoidal method.
Q2) Compute the value of 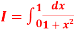 ?
?
A2)
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
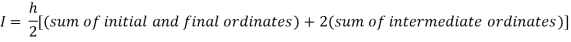
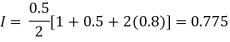
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
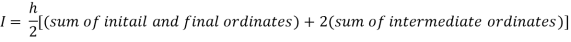
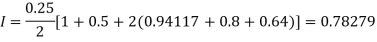
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
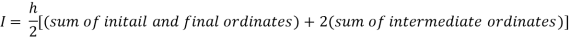
 [(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
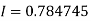
Q3) Evaluate, using trapezoidal rule with five ordinates
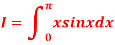
A3)
Here 
We construct the data table:
X | 0 |  | 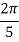 | 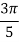 | 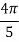 | 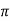 |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
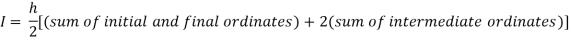
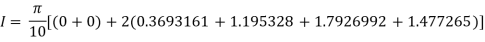
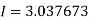
Q4) What do you understand by Simpson’s 1/3rd rule?
A4)
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that 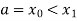 <
<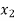 <…. <
<…. <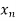 =b.
=b.
Here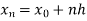 .
.
To find the value of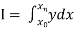 .
.
Setting n = 2,
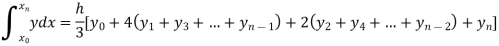
Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected a so f(x) is a polynomial of degree 2.
Q5) Estimate the value of the integral

By Simpson’s rule with 4 strips and 8 strips respectively.
A5)
For n=4, we have 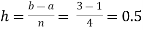
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
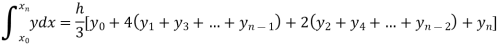
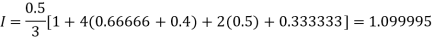
For n = 8, we have 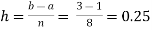
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule
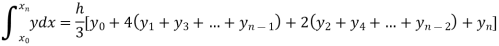
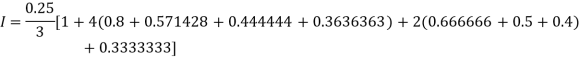
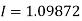
Q6) Evaluate 
A6)
Using Simpson’s 1/3 rule with 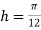 .
.
For 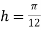 , we construct the data table:
, we construct the data table:
X | 0 |  |  |  |  | 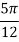 |  |
 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule
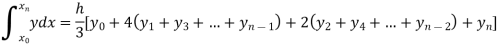
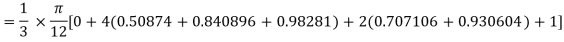
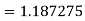
Q7) Evaluate 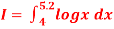 By Simpson’s 3/8 rule.
By Simpson’s 3/8 rule.
A7)
Let us divide the range of the interval [4, 5.2] into six equal parts.
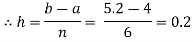
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
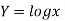 | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
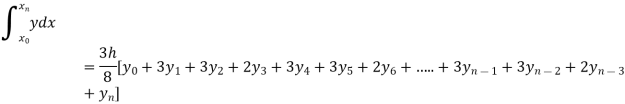

= 1.8278475
Q8) Evaluate 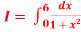
A8)
Let us divide the range of the interval [0,6] into six equal parts.

For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
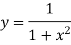 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
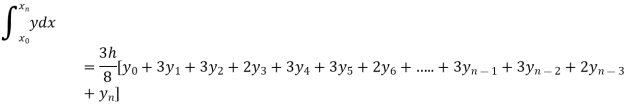
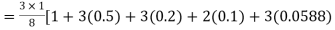 +3(0.0385) +0.027]
+3(0.0385) +0.027]
=1.3571
Q9) Evaluate 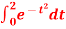
A9)
Here 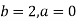
Using 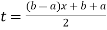 =
=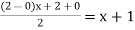
Also 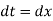
For 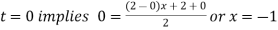
For 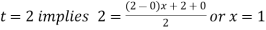
Hence 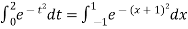
Here 
By Gauss quadrature 3-point rule
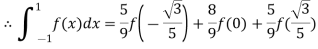
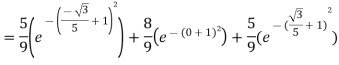
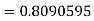
Q10) Evaluate 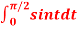 by 2-point Gaussian rule.
by 2-point Gaussian rule.
A10)
Here 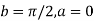
Using  =
=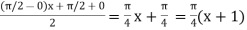
Also 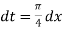
For 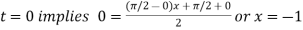
For 
Hence 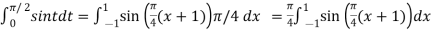
Here 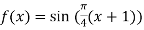
By Gauss quadrature 2-point rule
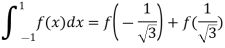
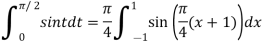
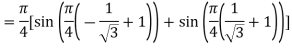
=0.99847
Q11) Solve by Gauss quadrature 3-point method 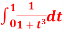
A11)
Given 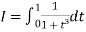
Here 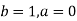
Using 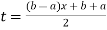 =
=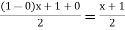
Also 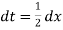
For 
For 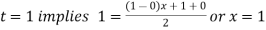
Hence 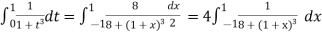
Here 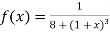
By Gauss quadrature 3-point rule
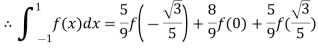
Hence 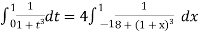
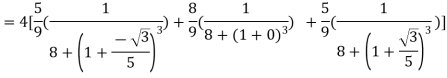
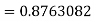
Q12) Evaluate 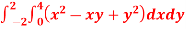
A12)
Let 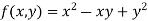
Here the interval of x and y are 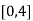 and
and 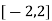 .
.
Let 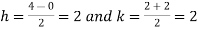
Consider the following table:
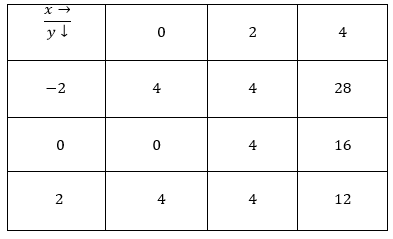
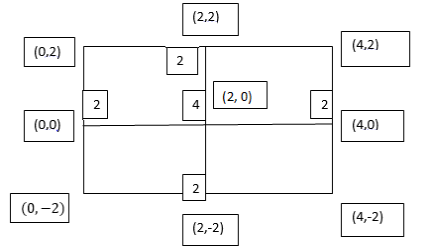
By Trapezoidal Rule
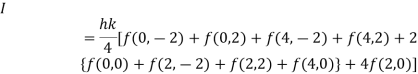

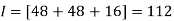 .
.
Q13) Evaluate 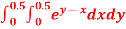
A13)
Let 
Here 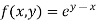
Let the number of intervals be 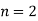 .
.
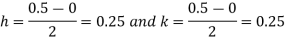
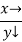 |
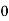 |
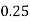 |
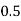 |
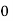 |
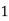
|
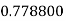 |
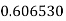 |
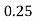 |
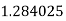 |
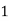 |
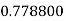 |
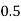 |
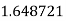 |
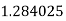 |
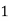 |
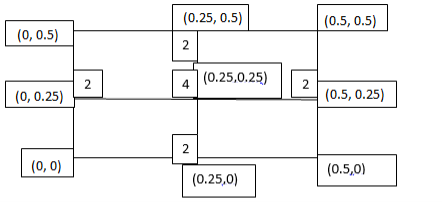
By Trapezoidal Rule


 .
.
Q14) Evaluate 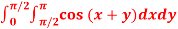
A14)
Let 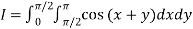
And 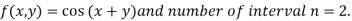
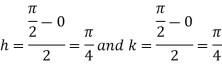
 |
 |
 |
 |
 |
 |
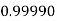 |
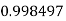 |
 |
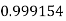 |
 |
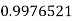 |
 |
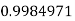 |
 |
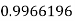 |
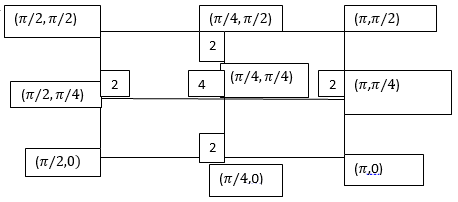
By Trapezoidal Rule
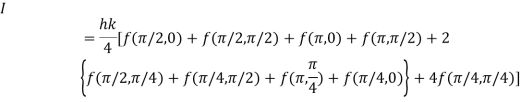

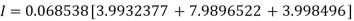
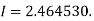
Q15) Evaluate 
A15)
Let 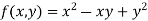
Here the interval of x and y are 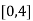 and
and 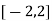 .
.
Let 
Consider the following table:
 |
 |
 |
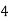 |
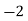 |
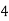
|
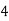 |
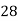 |
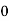 |
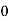 |
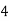 |
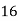 |
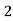 |
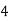 |
 |
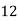 |
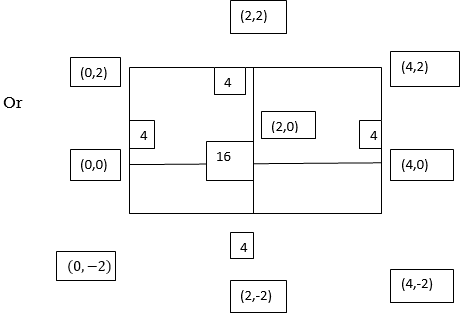
By Simpson’s 1/3 Rule
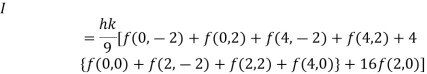

 .4444444
.4444444
Q16) Evaluate 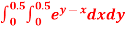
A16)
Let 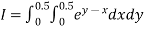
Here 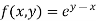
Let the number of intervals be  .
.
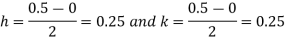
 |
 |
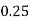 |
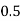 |
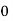 |
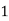
|
 |
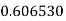 |
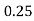 |
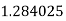 |
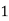 |
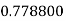 |
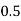 |
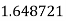 |
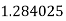 |
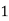 |
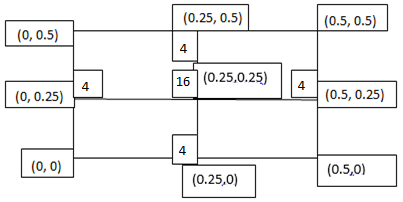
By Simpson’s 1/3 Rule
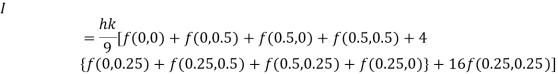

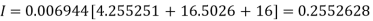
Q17) Evaluate 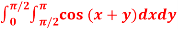
A17)
Let 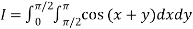
And 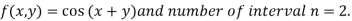

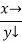 |
 |
 |
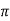 |
 |
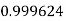 |
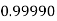 |
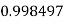 |
 |
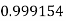 |
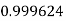 |
 |
 |
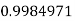 |
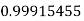 |
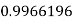 |
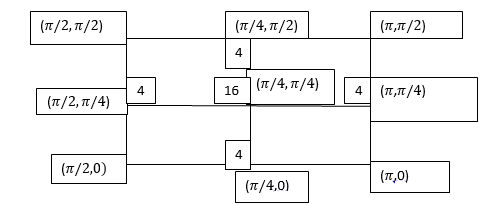
By Simpson’s 1/3 Rule