Unit – 6

Probability and Linear Algebra

Q1) What do you understand by two dimensional random variable?

A1)

Let X and Y be two discrete random variables defined on the sample space S of a random experiment then the function (X, Y) defined on the same sample space is called a two-dimensional discrete random variable. In others words, (X, Y) is a two-dimensional random variable if the possible values of (X, Y) are finite or countably infinite. Here, each value of X and Y is represented as a point (x, y) in the xy-plane.

Q2) Define joint probability mass function.

A2)

Let (X, Y) be a two-dimensional discrete random variable. With each possible

Outcome (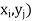we associate a number p (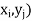representing

Where P [X = 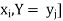satisfies the following conditions-

1. p (
2. 

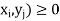
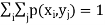
The function ‘p’ is called joint probability mass function of X and Y.

If (X, Y) is a discrete two-dimensional random variable which take up the

Values (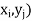 then the probability distribution of X is-

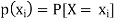
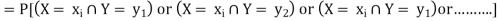
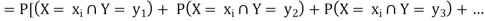
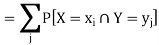
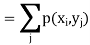
Which is known as the marginal probability mass function of X. Similarly, the

Probability distribution of Y is

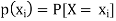
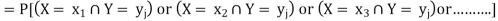
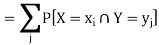
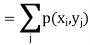
And is known as the marginal probability mass function of Y.

Q3) A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.

A3)

We consider the following events:

A: Selected item comes from A.

B: Selected item comes from B.

D: Selected item is defective.

We are looking for 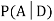. We know:

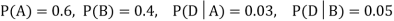
Now,

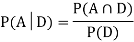
So, we need

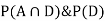
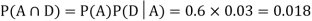
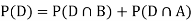
Since, D is the union of the mutually exclusive events 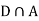and (the entire sample space is the union of the mutually exclusive events A and B)

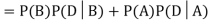
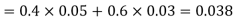
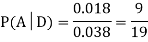
Q4) Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball drawn is red find the probability that it is drawn from the first urn.

A4)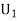
: The ball is drawn from urn I.

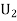: The ball is drawn from urn II.

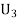: The ball is drawn from urn III.

R: The ball is red.

We have to find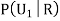

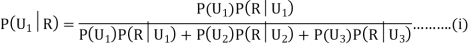
Since the three urns are equally likely to be selected

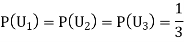
Also,

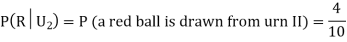
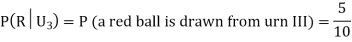
From (i), we have

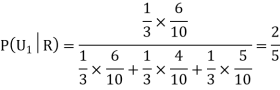
Q5) Define Bayes theorem.

A5)

Let S be a sample space and 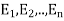be n mutually exclusive events with P (.

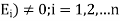Let A be an event which is a sub-set of 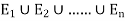with P(A)>0, then-

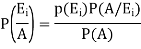
Where i = 1, 2, ……. ,n

And 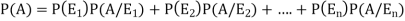[which is the law of total probability]

Q6) Three urn contains 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected randomly and a ball is drawn from it.

If the ball drawn is red then find the probability that it is drawn from the first urn.

A6)

Let,

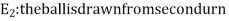
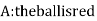
Now we have to find-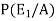

By using Bayes theorem-

= 

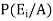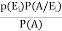
Here three urns equally likely to be selected-

So that-

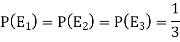
And-

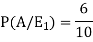
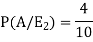
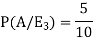
So that-

= 

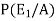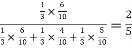
Hence the required probability is 2/5.

Q7) What do you understand by the independence of events?

A7)

Events are said to be independent if happening or non-happening of any one event is not affected by the happening or non-happening of other events. For example, if a coin is tossed certain number of times, then happening of head in any trial is not affected by any other trial i.e., all the trials are independent.

Two events A and B are independent if and only if P(B|A) = P(B) i.e., there is no relevance of giving any information. Here, if A has already happened, even then it does not alter the probability of B.

If A and B are independent events then-

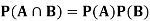
(Two disjoint events are not independent.)

Independence implies that

Knowing that outcome is in B does not change your perception of the outcome’s being in A.

Q8) Two cards are drawn from a pack of cards in succession with replacement of first card. Find the probability that both are the cards of ‘heart’.

A8)

Let A be the event that the first card drawn is a heart card and B be the event that second card is a heart card.

As the cards are drawn with replacement,

Here A and B are independent and hence the required probability

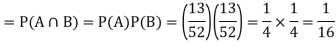
Q9) A class consists of 10 boys and 40 girls. 5 of the students are rich and 15 students are brilliant. Find the probability of selecting a brilliant rich boy.

A9)

Let A be the event that the selected student is brilliant, B be the event that he/she is rich and C be the event that the student is boy.

P(A) = 15/50, P(B) = 5/50 and P(C) = 10/50,

Hence the required probability- [ A, B, C are independent events]

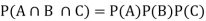
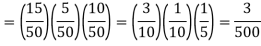
Q10) A die is rolled. If the outcome is a number greater than 3, what is the probability that it is a prime number?

A10)

The sample space of the experiment is

S = {1, 2, 3, 4, 5, 6}

Let A be event that the outcome is a number greater than 3 and B be the event that it is a prime number.

A = {4, 5, 6}, B = {2, 3, 5} and hence

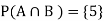
P(A) = 3/6, P(B) = 3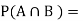/6, 1/6.

The required probability = P(B|A)

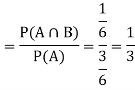
Q11) What is mathematical expectation?

A11)

Let a random variable X has a probability distribution which assumes the values say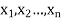 with their associated probabilities 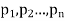then the mathematical expectation can be defined as-

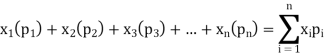
The expected value of a random variable X is written as E(X).

The expected value for a continuous random variable is

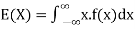
The mean value (μ) of the probability distribution of a variate X is commonly known as its expectation current is denoted by E (X).

Q12) If a random variable X has the following probability distribution in the tabular form, then what will be the expected value of X.

A12)

We know that-

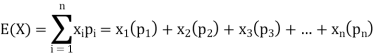
So that-

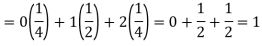
Q13) If it rains, a rain coat dealer can earn Rs 500 per day. If it is a dry day, he can lose Rs 100 per day. What is his expectation, if the probability of rain is 0.4?

A13)

Let X be the amount earned on a day by the dealer. Therefore, X can take the values Rs 500, -Rs 100

Loss of 100 Rs is equivalent to -100 Rs

Hence the expectation of the amount earned-

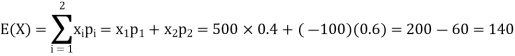
Thus, his expectation is Rs 140, i.e., on an overage he earns Rs 140 per day.

Q14) What is the discrete probability distribution?

A14)
Let X be a discrete variate which is the outcome of some experiments. If the probability that X takes the values of x is 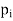, then-

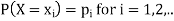
Where-

1.

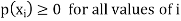
2.

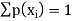
The set of values 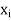with their probabilities 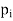makes a discrete probability distribution of the discrete random variable X.

Probability distribution of a random variable X can be exhibited as follows-

X		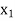	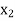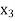and so on
P(x)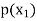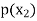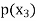

Q15) Find the probability distribution of the number of heads when three coins are tossed simultaneously.

A15)

Let be the number of heads in the toss of three coins

The sample space will be-

{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Here variable X can take the values 0, 1, 2, 3 with the following probabilities-

P [X= 0] = P[TTT] = 1/8

P [X = 1] = P [HTT, THH, TTH] = 3/8

P [X = 2] = P [HHT, HTH, THH] = 3/8

P [X = 3] = P[HHH] = 1/8

Hence the probability distribution of X will be-

X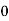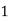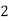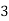
P(x)

Q16) The probability density function of a variable X is

(i)                Find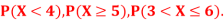

(ii)             What will be e minimum value of k so that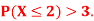

A16)

(i) If X is a random variable, then

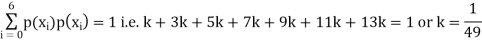
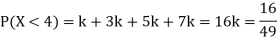
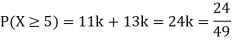
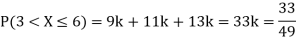
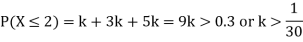
(ii) Thus, minimum value of k=1/30.

Q17) Show that the following function can be defined as a density function and then find .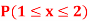

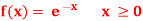
A17)

Here

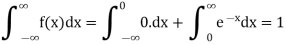
So that, the function can be defined as a density function.

Now.

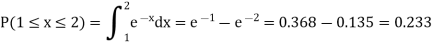
Q18) Let X be a continuous random variable with PDF

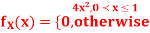
Find .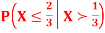

A18)

We have

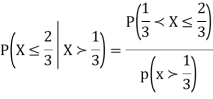
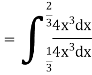
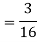
Q19) If on an average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.

A19)

Out of 10 ships one ship is wrecked.

i.e., nine ships out of 10 ships are safe, P (safety) =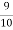

P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P (5)

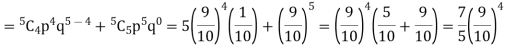
Q20) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?

A20)

The probability that a man aged 60 will live to be 70

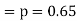
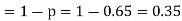
Number of men= n = 10

Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)

= P (7) + P (8) + P (9) + P (10) =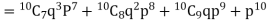

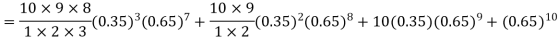
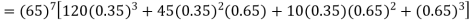
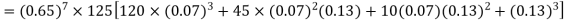
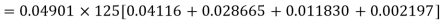
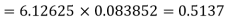
Q21) Buses are scheduled every 5 minutes at a certain bus stand. A person comes to the stand at a random time. Let the random variable X count the number of minutes he/she has to wait for the next bus. Assume X has a uniform distribution over the interval (0, 5). Find the probability that he/she has to wait at least 3 minutes for the bus.

A21)

As X follows uniform distribution over the interval (0, 5), probability density function of X is

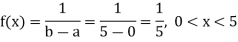
Thus, the desired probability

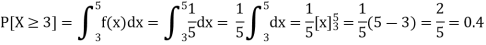
The probability that he/she has to wait at least 3 minutes for the bus is 0.4.

Q22) Assume that the probability of an individual coal miner being killed in a mine accident during a year is . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.

A22)

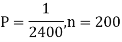
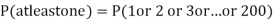
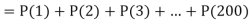
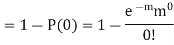
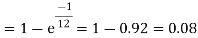
Q23) If cars arriving at workshop follow the Poisson distribution. If the average number of cars arrivals during a specified period of an hour is 2.

Find the probabilities that during the given hour-

1. No car arrive

2. At least two cars arrive.

A23)

Here the average of car arrivals is - 2

So that mean = 2

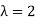
Let X be the number of cars arriving during the given hour,

By using Poisson distribution, we get-

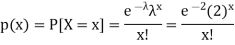
So that the required probability-

1. P [no car will arrive] = P [X = x] =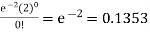

2. P [At least two cars will arrive] = P [X≥2] = P [X =2] + P [X = 3] + ……….

= 1 - P [[X =1] + P [X =0]]

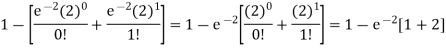
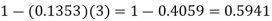
Q24) What is the normal distribution?

A24)

The concept of normal distribution was given by English mathematician Abraham De Moivre in 1733 but the concrete theory was given by Karl Gauss that is why sometime normal distribution is called Gaussian distribution.

Normal distribution is a continuous distribution. It is derived a s the limiting form of the Binomial distribution for large values of n and p and q are not very small.

The Normal distribution is given by the equation

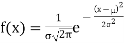  …. (1)

Where =mean, 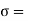standard deviation,

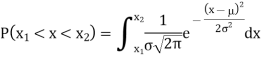
On substitution 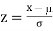in (1), we get  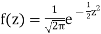 …. (2)

Here mean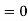, standard deviation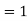

(2) is known as standard form of normal distribution.

Q25) X is a normal variate with mean 30 and S.D. 5, find the probabilities that

(i)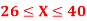               

(ii)            

(iii)          |X-30|≥5

A25)

We have μ =30 and 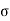=5

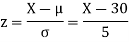
(i)                When X = 26, z = -0.8, when X =40, z =-2

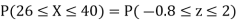
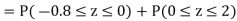
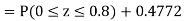
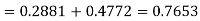
(ii)              When X =45, z =3

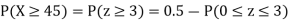
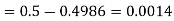
(iii)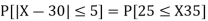          

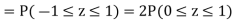
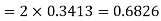
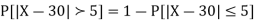
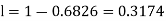
Q26) In a normal distribution 31% of the items are under 45 and 8% are over 64. Find the mean and standard deviation of the distribution.

A26)

Let 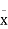be the mean and 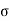the standard deviation 31% of the items are under 45 means area to the left of the ordinate x = 45

When x = 45, let z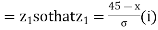

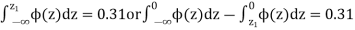
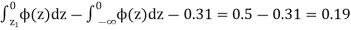
From table III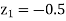

When x = 64, let so that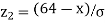

Hence,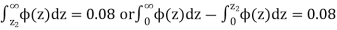

From table III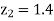

From (i) and (ii),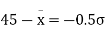

From (iii) and (iv),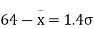

Solving these equations, we get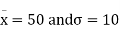

Q27) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine, assuming the diameters are normally distributed.

A27)

Here-

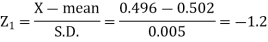
And

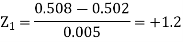
Area for non-defective washers = area between z = -1.2 to +1.2

= 2 area between z = 0 and z = 1.2

= 2 × 0.3849 = 0.7698 = 76.98%

Then percent of defective washers = 100 – 76.98 = 23.02 %