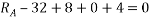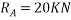Unit- 2
Equilibrium
Que-1 Determine tension chord AB and BC for equilibrium of 20kg block shown in given fig
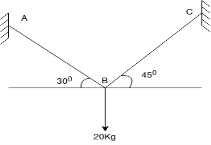
Ans- 6 F.B.D for given system
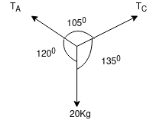
By lami’s theorem
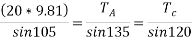
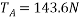
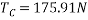
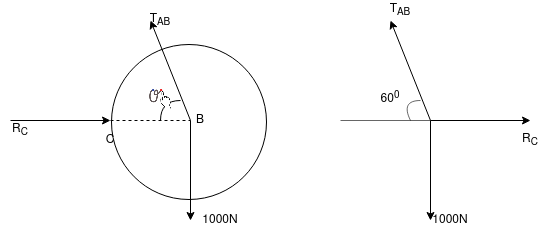
Que-2 A circular roller of 1000N weight and 20cm radius hang by tie rod AB= 40cm and rest against a smooth vertical wall at C as shown in fig.
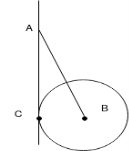
Determine :- the tension in rod and reaction at point C .
Ans- FBD diagram for given system
=
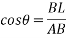
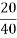
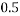
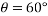
By lami’s theorem
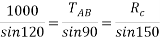
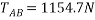
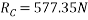
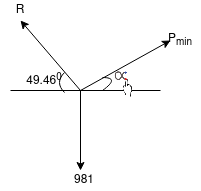
Que-3 Determine the force P applied at 30
to horizontal just necessary to start a roller having 50cm radius over a 12 cm high obstruction if roller is 100 kg mass shown in fig. Below . Also find magnitude and direction of P when it is minimum.
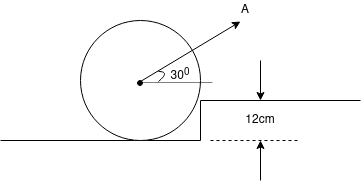
Ans-8 F.B.D for roller
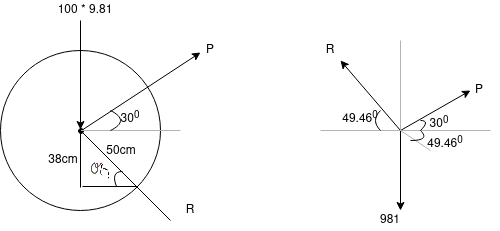
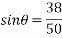
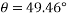
By lami’s theorem
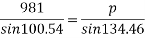
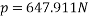
To final p min
By lami’s theorem
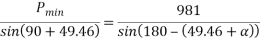
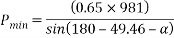
For 
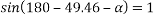
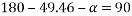
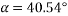
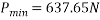
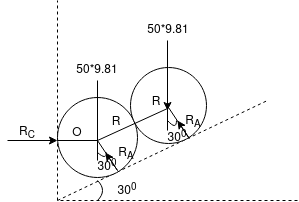
Ques 4 Two identical rollers each of mass 50Kg are supported by an inclined plane and vertical wall as shown in Fig. Assuming smooth surfaces Find reactions induced at the point of support A,B and C
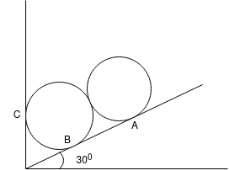
Ans Consider FBD of both rollers and let R be the radius of rollers
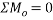
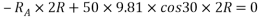
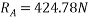
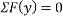
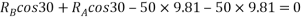
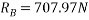
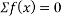
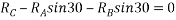
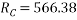
Ques 5 Two spheres A and B of 1000N and 750N weight respectively are kept as shown in figure Determine reactions at all contact points P,Q,R,S
Radius of A=400mm
Radius of B=300mm
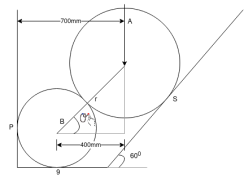
Ans Consider F.B.D. Of sphere A
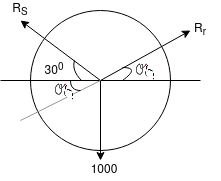By Lami’s theorem
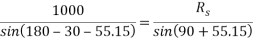
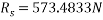
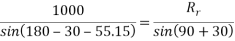
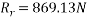
Consider F.B.D. Of sphere B
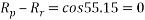
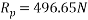
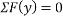
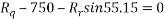
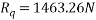
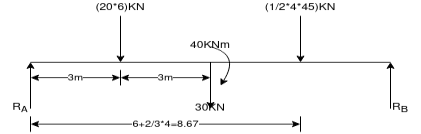
Ques 6 Calculate support reactions for beam as shown in figure
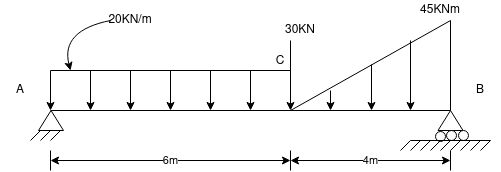
Ans – consider F.B.D of beam AB
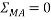
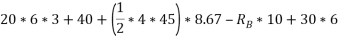
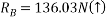
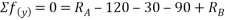
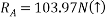
Que-7 Find support tractions at A and F for given fig.
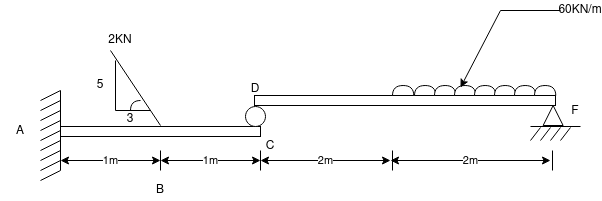
Ans- consider FBD for beam DF
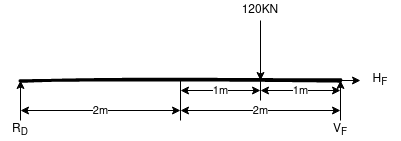
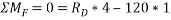
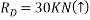
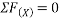
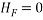
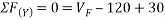
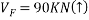
Consider F.B.D for beam AC
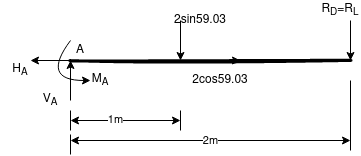
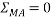
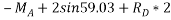
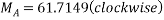
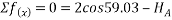
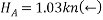
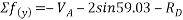
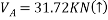
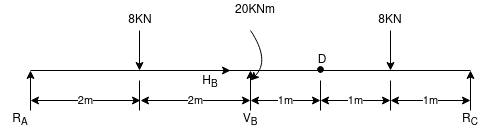
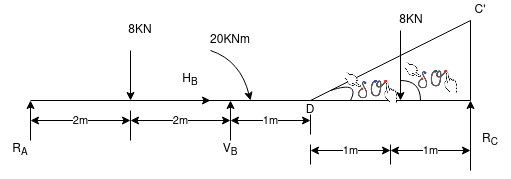
Que-8 Calculate reaction at supports A,B,C of beam loaded as shown in fig. Below by principle of virtual work
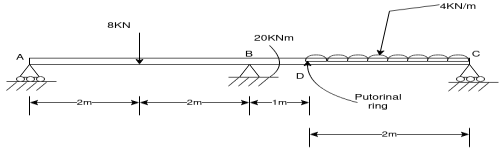
Ans - F.B.D for given system
Lift end C about point D such that DC rotates by 
By principle of virtual work
Total work done =0
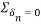
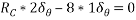
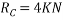
Lift internal hing D such that portion AD rotates by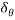 
about A and potions CD rotates by 
about C
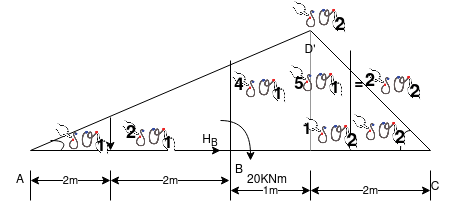
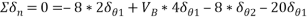
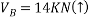
Lift the entire beam AC vertically up by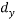 
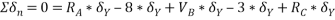
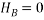
Since there is no horizontal force
Que-9 Determine the reaction 
in overhanging beam as shown in fig. Below by vertical work method.
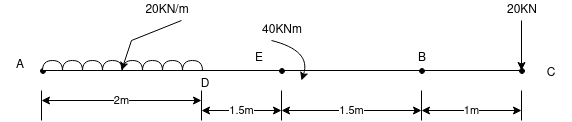
Ans-let us given virtual displacement 
at A
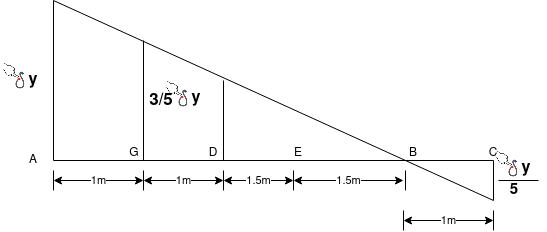
Displacement at AB 
Displacement at centroid of udl =
=0.8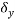
Displacement at B=0
Displacement at C B
Rotation of moment =
Writing virtual work equation for system
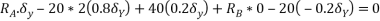
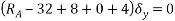
Since 
