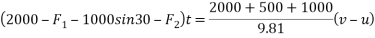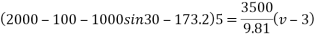Unit-04
Kinetics of linear
Que-1 A 50 kg block kept on the top of 15 shopping surface in pushed down the plane with an initial velocity of 20 m/s if u=0.4 determine distance travel by block and time it will take as it come to rest .
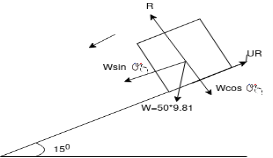
Ans - consider FBD of block
By newton’s 2nd law
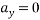
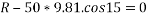
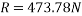
Friction force =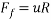
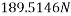
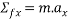
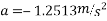
We know
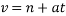
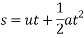
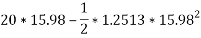
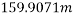
Que-2 An election being lowered into a mine shaft starts from rest and attains a speed of 10m/s within a distance of 15m. The elevator alone has a mass of 500kg and it carries a box of 600kg mass in it. Find the total tension in cables supporting the elevator , during this acceleration motion. Also find total forces between box and floor of elevator .
Ans- consider F.B.D elevator with box
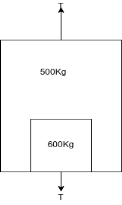
We know
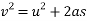
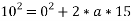
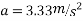
By newton’s 2nd law
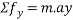
Consider FBD of box
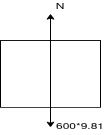
Let N =normal reaction exerted between before box and floor of elevator
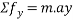
Que-2 At a given instant the 50N block AB moving downward with speed of 1.8 m/s . Determine its speed 2 sec later . block B has a 20N weight and coefficient of friction block B and horizontal plane is 0.2 neglect the mass of pulley’s and chord use D’ alemeberts principle
Ans- consider FBD of block A
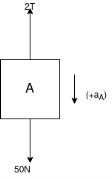
Force acting on block A tension (2T) 
Weight of block A ( 
Resultants force acting on block A= 2T -50----1
Since block B moving downward with acceleration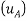 
Force acting on block =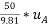
-----2
Equating 1 and 2
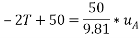
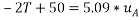
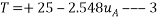
Consider FBD of block B
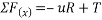
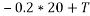
---4
Since block B moving with acceleration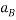 
Force acting on block = 
=2.03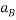 
----5
Equating 4 and 5
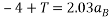
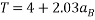---6
We know ,
Kinematic relation between block A and B
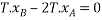
Differentiating w.r.t
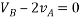
Again differentiating w.r.t
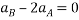
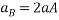
Solving 3 and 4
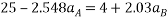
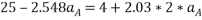
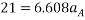
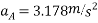
Speed of block A after 2 sec is given by
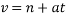
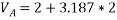
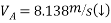
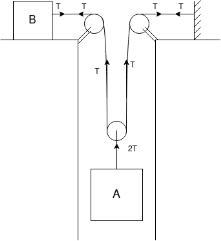
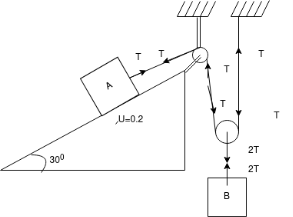
Que-3 Block A of 400kg mass is being pulled up the inclined plane by using block B of 80kg mass as shown in fig. Determine the acceleration of block B and tension in rope pulling block A. Take u=0.2 assume ropes are inextensible and pulley’s are small , frictionless and massless.
Ans- kinematic relation
By virtual work principle
Total virtual work done by internet forces (tension)=0
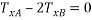
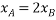
Differentiating w.r.t
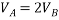
Again differentiating w.r.t
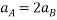
Consider FBD block A
Forces acting on block A tension T acting upward . Frictional force=uR acting downward 
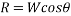
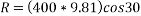
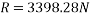
Resultant force acting on block A =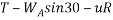 
As block moves with acceleration 
Force acting on block A = 400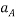
Force acting on block A = 400* 
Equating equation 1 and equation 2
----3
Consider F.B.D for block B
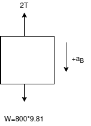
Resultant force acting on block B = 2T -7848—4
As block B moves with acceleration 
Force acting on block B= 800*
Equating 4 and 5
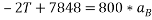
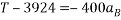
Solving 3 and 4
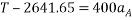
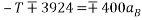
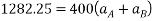
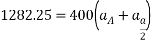
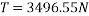
Que- 4 Block A has mass of 2kg and velocity of 5m/s up the plane shown in fig. V using principle of work -energy locate the rest position of block
Ans – consider FBD for block A
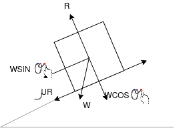
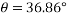
Friction force=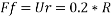
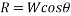
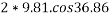
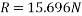
By principle of work -energy
Work done =change in K.E
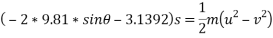
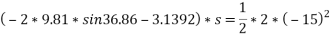
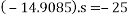
Que-5 1. Determine the distance in which can moving at 90 km/h can come to rest after pointer B switched off if u between tyres and road B 0.8.
2. Determine also max allowable speed of car if it B to stop in same distance as above on ice road where u between tyre and road is 0.08
Ans – i. u=0.8
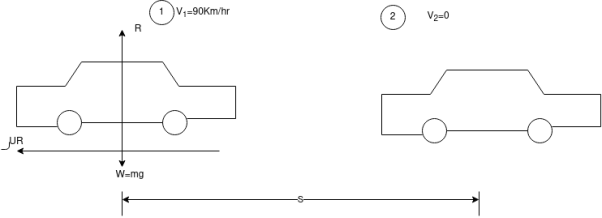
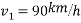
=25m/s.
By work -energy principle
Work done = change in kinetic energy
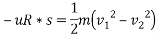
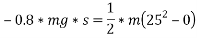
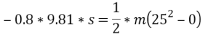
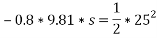
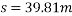
Ii. For ice road
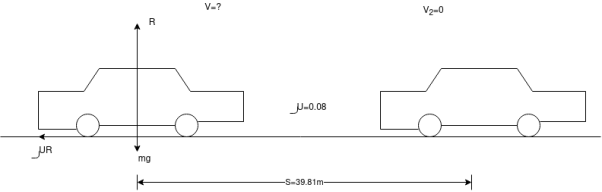
u=0.08
By work energy principle
Work done=change in K.E
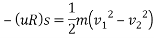
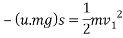
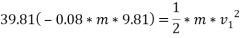
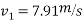
Que-6 A pile hammer weighing 15 KN drops from height of 600mm on a pile 7.5KN. How deep a single blow of hammer drive the pile if resistance to pile is 140KN assume ground resistance is constant
Ans- velocity of hammer at time of strike
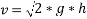
=3.431m/s
Let V be the velocity of pile and hammer immediately after impact . Applying principle of conservation of momentum of system of pile and pile hammer.
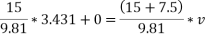
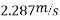
Now applying work-energy equations to system
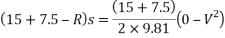
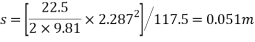
Ques 7 The system shown in fig has a rightward velocity of 8m/s. Determine velocity after 5 second. Take 
for surface in contact Assume pulleys to be frictionless
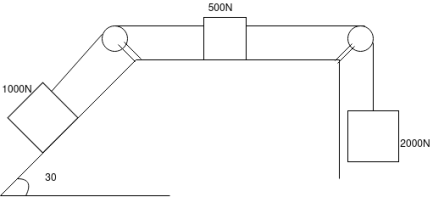
Ans
Consider FBD for system
Writing impulse-momentum equation
