Unit 6
Impact and collision
Q1)1 State difference between elastic and plastic collision.
Ans.
Elastic collision | Plastic collision |
Total kinetic energy is conserved | The total kinetic energy of bodies at beginning and end of impact is different |
Momentum does not change | Momentum does change |
No conservation of energy take place | Kinetic energy is changed into other energy such sound or heat energy |
Q2) 2 State and explain
1) Law of conservation of momentum
2) Newton's law of motion of elastic bodies
Ans. Law of conservation of momentum
It states that, “The total momentum of two bodies remains constant after their collision or any other mutual action.”
Mathematically,
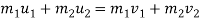
Where
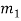 =mass of first body
=mass of first body
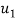 =initial velocity of first body
=initial velocity of first body
 =final velocity of first body
=final velocity of first body
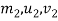 =corresponding values for second body.
=corresponding values for second body.
Newton's law of collision of elastic bodies
Its state,” when two moving bodies collide with each other, their velocity of separation there's a constant ratio to their velocity of approach.”
Mathematically,
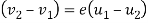
Where,
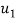 =initial velocity of first body
=initial velocity of first body
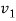 =final velocity of first body
=final velocity of first body
 =corresponding values for second body
=corresponding values for second body
e=constant of proportionality, also known as coefficient of restitution.
Q3) 3 Define
1) Time of compression
2) Time of restitution
3) Time of collision
4) Coefficient of restitution
Ans. Time of compression
The time taken by two bodies in compression after the instant of collision is known as time of compression.
Time of restitution
The time taken by two bodies to regain the original shape after compression is known as time of restitution.
Time of collision
The sum of time of compression and time of restitution is known as time of collision or period of collision or period of impact.
Coefficient of restitution:-
It is defined as the ratio of velocity of separation (of to moving bodies collide with each other) to their velocity of approach.
It is also defined as the ratio of relative velocities of colliding bodies after impact to their relative velocity before impact.
It is denoted by symbol 'e'
The relative velocities are measured along the line of impact which is the common normal to colliding surfaces.
Consider two bodies A and B having direct impact as shown in figure 1
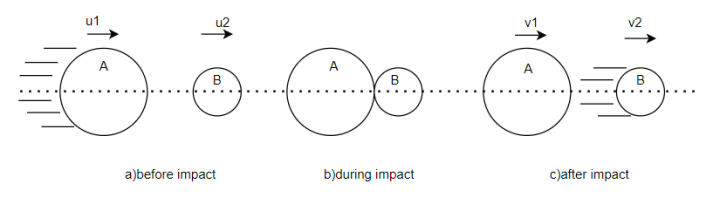
Let,
 =initial velocity of body A
=initial velocity of body A
 =final velocity of body A
=final velocity of body A
 =corresponding values for body B
=corresponding values for body B
The impact will take place only if 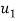 is greater than
is greater than 
Velocity of approach=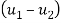
After impact separation will take place only if  is greater than
is greater than 
Velocity of separation=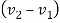
According to Newton’s law of origin for elastic bodies
Velocity of separation=e× velocity of approach
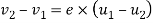
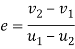
Where
e=constant of proportionality and is called coefficient of restitution
Its value lies between 0 and 1
If e=0 => two bodies are inelastic
If e=1 => two bodies are perfectly elastic
Q4)4 Write note on
1) Direct impact
2) Indirect impact
Ans. Direct impact:-
The line of impact of two colliding bodies is the line joining the centres of these bodies and passes through the point of contact as point of collision as shown in figure 2
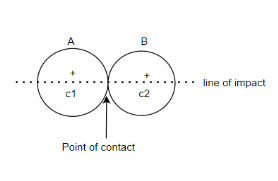
According to law of conservation of momentum
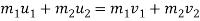
Indirect impact of two bodies
If two bodies before impact are not moving along the line of impact the collision is called indirect (or oblique) impact. As shown in figure 3
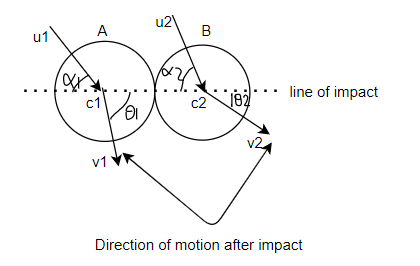
The Newton's law of collision of elastic bodies also hold good for indirect impact.
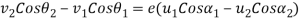
Q5)5 Two particles of masses 10kg and 20kg are moving along a straight line towards each other at velocities of 4m/s and 1 m/s respectively. If e=0.6. Determine the velocities of particles immediately after their collision. Also find loss in kinetic energy.
 Ans.
Ans.
By law of conservation of momentum
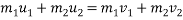
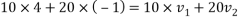
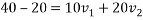
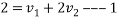
Also,
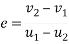
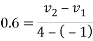
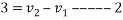
Equation 1 and equation 2
1+2
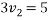
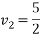
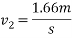
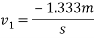
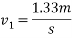
Loss in kinetic energy=initial kinetic energy-final kinetic energy
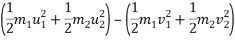
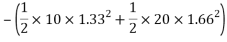
=90-36.67
=53.335
% loss in K.E.=(
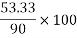
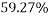
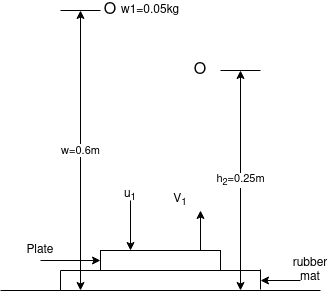
Q6) 6 A 50gm ball is dropped from height of 600 mm on a small plate. It rebound to height 400mm when played directly rest on ground and to height of 250mm when a form rubber mat is placed between plate and ground.
Determine
1) Coffee shirt off of restitution between and ground
ground
2) Mass of plate
Ans.
The plate is kept directly on ground.
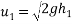
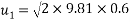
=3.43m/s
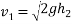
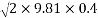
 =2.8m/s
=2.8m/s
Coefficient of restitution=e=
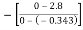
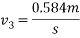
3) Bye law conservation of momentum
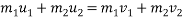
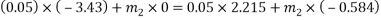
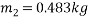
Q7) 7 A 900kg car B travelling 48km/hr couples to 680Kg car travelling 24km/hr in same directions. What is their common speed after coupling
Ans. By Law of conservation of momentum
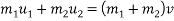
V=37.67km/hr
Q8)8 A ball is dropped from height  smooth floor knowing that for first bounce
smooth floor knowing that for first bounce  . Determine
. Determine
1) Coefficient of restitution
2) Height of second bounce
Ans. 
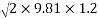
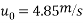
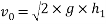
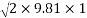
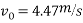
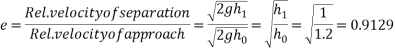
Now for second bounce
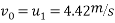
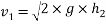
We know that
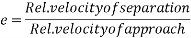
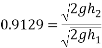
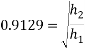
Squaring on both sides
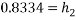
Q9)9 Three perfectly elastic ball A,B and C of masses 2Kg, 4Kg and 8Kg move in the same direction with velocity of 4m/s, 1m/s and 0.75m/s respectively. If ball A impinges with ball B which in turn impinges with ball C, prove that balls A and B will bought to rest by impacts.
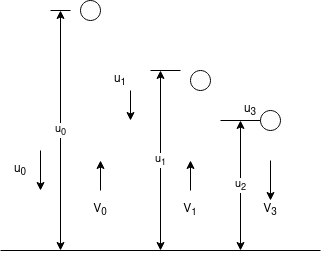 Ans. Given
Ans. Given
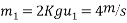
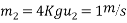
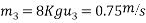
Let  be final velocities after impact of ball A and ball B.
be final velocities after impact of ball A and ball B.
By Law of conservation of momentum
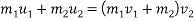
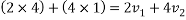
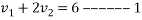
We also know that
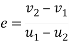
For perfectly elastic collision e=1
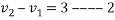
Solving equation 1 and 2
Equation 1+Equation 2
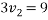
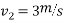
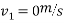
Thus first ball A will brought to rest by impact of ball A and ball B.
Now
For final velocity of ball B
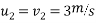
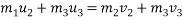
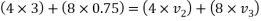
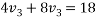
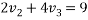
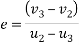
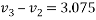
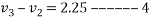
Solving equation 3 and 4
3+2*4
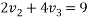
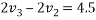
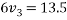
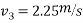
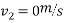
We can say that ball B is brought to rest after impact with ball C.
Q10)10 Two balls A and B are travelling along same straight path in opposite direction. Sphere A of mass 1.2 kg is moving with 5m/s toward right and sphere is of mass 2.4kg is moving with 2.5m/s towards left. If e=0.8 determine their final velocity
Ans.

By law of conservation of momentum
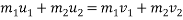
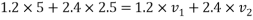
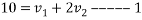
Also
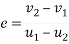
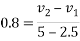
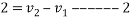
Solving eqn 1 and 2
1+2
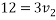
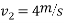
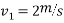
Q11)11 A ball drop from height of 9m upon horizontal slab. If it rebound to height of 5.76m. Show that coefficient of restitution is 0.8.
Ans. We know that
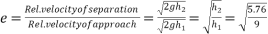

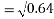
=0.80