Unit 2

Eigen Values and Eigen vectors

1. Find the sum and the product of the Eigen values of ?

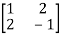      The sum of Eigen values =  the sum of the diagonal elements

   =1+(-1)=0

     The product of the Eigen values is the determinant of the matrix

       On solving above equations we get

2.     Find out the Eigen values and Eigen vectors of ?

The Characteristics equation is given by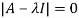

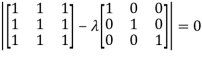
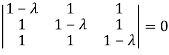
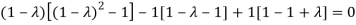
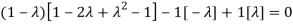
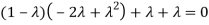
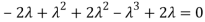
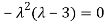
                                          Or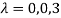

Hence the Eigen values are 0,0 and 3.

The Eigen vector corresponding to Eigen value is

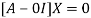
Where X is the column matrix of order 3 i.e.

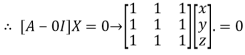
This implies that

Here number of unknowns are 3 and number of equation is 1.

Hence we have (3-1)=2 linearly independent solutions.

Let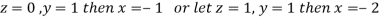

Thus the Eigen vectors corresponding to the Eigen value 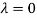are (-1,1,0) and (-2,1,1).

The Eigen vector corresponding to Eigen value 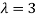is

Where X is the column matrix of order 3 i.e.

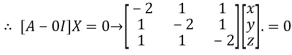
This implies that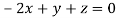

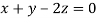
Taking last two equations we get

Or

Thus the Eigen vectors corresponding to the Eigen value are (3,3,3).

Hence the three Eigen vectors obtained are  (-1,1,0), (-2,1,1) and (3,3,3).

3.     Find out the Eigen values and Eigen vectors of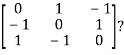

Let A =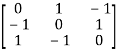

The characteristics equation of A is .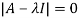

                                           Or 

                                                Or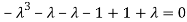 

                                                      Or

                                                       Or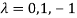

The Eigen vector corresponding to Eigen value 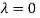is

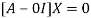
Where X is the column matrix of order 3 i.e.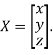

         Or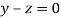

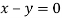
On solving we get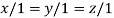 

Thus the Eigen vectors corresponding to the Eigen value is (1,1,1).

The Eigen vector corresponding to Eigen value 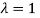is

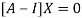
Where X is the column matrix of order 3 i.e.

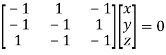
Or    

On solving or .

Thus the Eigen vectors corresponding to the Eigen value 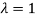is (0,0,2).

The Eigen vector corresponding to Eigen value 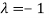is

Where X is the column matrix of order 3 i.e.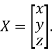

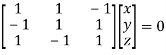
   Or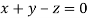    

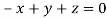
On solving we get 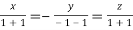   or .

Thus the Eigen vectors corresponding to the Eigen value is (2,2,2).

Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).

4.     Verify the Cayley-Hamilton theorem and find the inverse.

?

Let A =

The characteristics equation of A is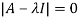

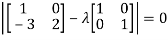
                                 Or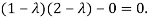

                                Or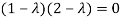 

                                 Or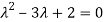 

By Cayley-Hamilton theorem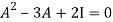 

                                   L.H.S: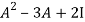

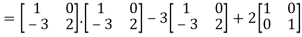
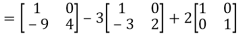
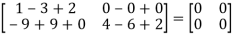                                                 =   =0=R.H.S

Multiply both side by on 

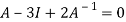
                                               Or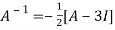

                                              Or [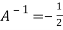

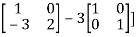
                                               Or

5.     Verify the Cayley-Hamilton theorem and find the inverse.

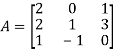
The characteristics equation of A is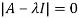

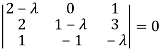
                                            Or

                                           Or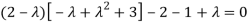

                                           Or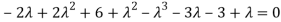

                                           Or

                                            Or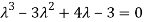

             By Cayley-Hamilton theorem

                L.H.S.

          =

=

=

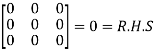
Multiply both side with 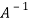in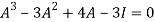

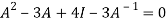
                                              Or

        Or

                     =

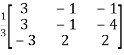
6.     Using Cayley-Hamilton theorem, find 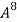, if A = ?

Let A =

The characteristics equation of A is

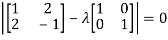
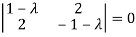
                                             Or

                                             Or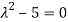

By Cayley-Hamilton theorem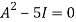   

L.H.S.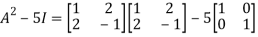

                          =

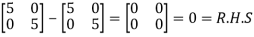
By Cayley-Hamilton theorem we have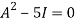   

            Multiply both side by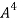

.

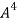
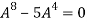
                     Or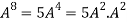 

                                 =

                                 =

7.     Write a short note on the property of eigen values?

   Properties of Eigen Values:

1. The  sum  of the  principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.

Let A be a matrix of order 3 then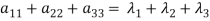

2.     The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then .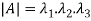

3.     If 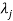is the Eigen value of the matrix A then 1/ 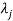is the Eigen value of the .

4.     If is the Eigen value of an orthogonal matrix, then 1/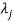 is also its Eigen value.

5.     If are the Eigen values of the matrix A then has the Eigen values .

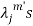8.     What do you understand by eigen values?

  Let A is a square matrix of order n. The equation formed by

Where I is an identity matrix of order n and 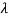is unknown. It is called characteristic equation of the matrix A.

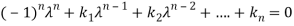
The values of the 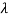are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.

Corresponding to each Eigen value there exist vectors X,

Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.

Note:   Corresponding to distinct Eigen value we get distinct Eigen vectors but in case of repeated Eigen values  we can have or not  linearly independent Eigen vectors.

If 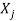is Eigen vectors corresponding to Eigen value 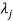then is also Eigen vectors for scalar c.