Unit - 3

Complex Numbers

1. Evaluate ( 1 + i )1000.

Solution:

Let z = 1 + i

We have to represent z in the form of r(cos θ + i sin θ).

Here,

Argument = θ = arc(tan (1/1) = arc tan(1) = π/4

Absolute value = r = (1)2+(1)2=2\sqrt{(1)^2 + (1)^2}= \sqrt{2}(1)2+(1)2​=2​

Applying DeMoivre’s theorem, we get

z1000 = [√2{cos(π/4) + i sin(π/4)}]1000

= 21000 {cos(1000π/4) + i sin(1000π/4)}

= 21000 {1 + i (0)}

= 21000
 

2.     Express five fifth‐roots of (√3 + i) in trigonometric form.

Solution:

We know, z = a + ib = r(cos x + i sin x)

Where r = a2+b2\sqrt{a^2+b^2}a2+b2​ and tan x = (b/a)

So,

Here r = 2 and θ = 30 degrees

Therefore, z = 2[cos(300 + 3600 k) + i sin cos(300 + 3600 k)]

Applying nth root theorem:

z1/5 = {2[cos(300 + 3600 k) + i sin cos(300 + 3600 k)]}1/5

= 21/5 [cos((300 + 3600 k)/5) + i sin cos((300 + 3600 k)/5)] …(1)

Where k = 0,1,2,3,4

At k = 0; (1)=> z1 = 21/5 [cos 60 + i sin 60]

At k = 1; (1)=> z1 = 21/5 [cos 780 + i sin 780]

At k = 2; (1)=> z1 = 21/5 [cos 1500 + i sin 1500]

At k = 3; (1)=> z1 = 21/5 [cos 2220 + i sin 2220]

At k = 4; (1)=> z1 = 21/5 [cos 2940 + i sin 2940]

3.     Write 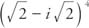in the form a + bi.

First determine the radius:

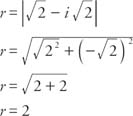
Since cos 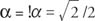and sin 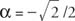, α must be in the fourth quadrant and α = 315°. Therefore,

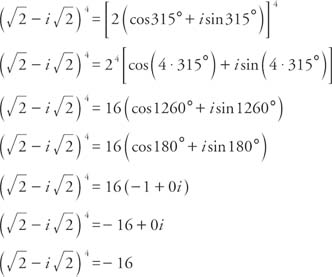
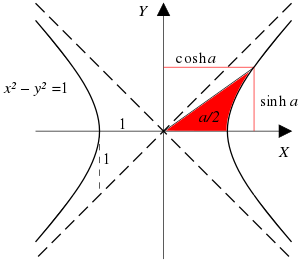
4.     Solve cosh2 x – sinh2 x

Solution:

Given: cosh2 x – sinh2 x

We know that

Sinh x = [ex– e-x]/2

Cosh x = [ex + e-x]/2

Cosh2 x – sinh2 x = [ [ex + e-x]/2 ]2 – [ [ex – e-x]/2 ]2

Cosh2 x – sinh2 x = (4ex-x) /4

Cosh2 x – sinh2 x = (4e0) /4

Cosh2 x – sinh2 x = 4(1) /4 = 1

Therefore, cosh2 x – sinh2 x = 1

5.     Find the inverse of the function f(x) = ln(x – 2)

Solution:

First, replace f(x) with y

So, y = ln(x – 2)

Replace the equation in exponential way , x – 2 = ey

Now, solving for x,

x = 2 + ey

Now, replace x with y and thus, f-1(x) = y = 2 + ey

6.     To solve an equation: f(x) = 2x + 3, at x = 4

Solution:

We have,

f(4) = 2 × 4 + 3

f(4) = 11

Now, let’s apply for reverse on 11.

f-1(11) = (11 – 3) / 2

f-1(11) = 4

Magically we get 4 again.

Therefore, f(f(4)) = f(4)

So, when we apply function f and its reverse f-1 gives the original value back again, i.e, f-1(f(x)) = x.