Unit - 4
Numerical Solution of linear simultaneous equations
Question and answer
- 2X+Y=4
X-3Y=9
X+4Y=-5
 The augmented matrix is.,
The augmented matrix is.,
2 1 4

 1 -3 9 r1 r2
1 -3 9 r1 r2
1 4 -5
 1 -3 9
1 -3 9
2 1 4-2r1+r2 & -r1+r3
1 4 -5

1 -3 9
0 7 -14 ( 1/7) r2 &( 1/7) r3
0 7 -14

1 -3 9
0 1 -2-1r2+r3
0 1 -2
1 0 3
0 1 -2
0 0 0
Here the final matrix we has reduced to echelon form and it also represents system of equations with x=3,y=-2.
2. X+y+z=5
2+3y=5z=8
4x+5z=2
So for the given above set of linear equations the Gauss-Jordan method represents as the following


1 1 15
2 3 58
4 0 52
 The augmented matrix is.,
The augmented matrix is.,
1 1 1
2 3 5
4 0 5
Now we reduce the above matrix in gauss Jordan form.

 2 3 5r2 r1
2 3 5r2 r1
 1 1 1r1 r2
1 1 1r1 r2
4 0 5

1 2 4r2 - 2r1
1 1 1
4 0 5
 1 2 4
1 2 4
1 1 1 r3 – r1
3 -2 1
So here represents the guass Jordan method by having a unique number one diagonally in the matrix.
3. X+y+z=3
2x+3y=7z=0
X+3y-2z=17

 The given set of linear equations can be written as.,
The given set of linear equations can be written as.,
1 1 1 3
2 3 7 0
1 3 -2 17
The augmented matrix o
For the given system of equations is.,

1 1 1
2 3 7
1 3 -2

 1 1 1
1 1 1
7 3 2c1c2
-2 3 1

1 1 1
 5 1 0r2 r2 - 2r1
5 1 0r2 r2 - 2r1
-2 3 1
So ,here the Gauss-Jordan method completes by making all the diagonal elements to unit number.
4. Use Jacobi’s method to solve the system of equations:
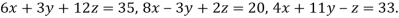
Since 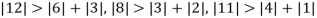
So, we express the unknown with large coefficient in terms of other coefficients.


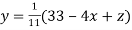 (1)
(1)

Let the initial approximation be 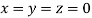
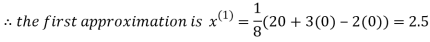
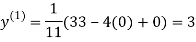
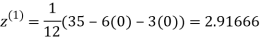
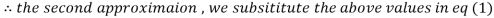
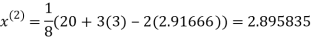
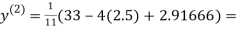 2.35606
2.35606
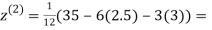 0.91666
0.91666
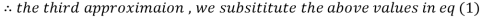
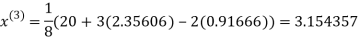
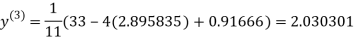
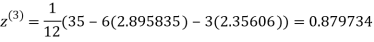

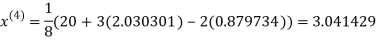
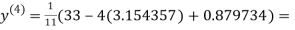 1.932936
1.932936
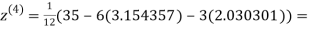 0.831912
0.831912
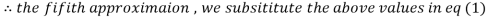
 3.016873
3.016873
 1.969654
1.969654


 3.010217
3.010217
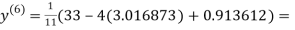 1.986010
1.986010


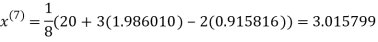
 1.988631
1.988631
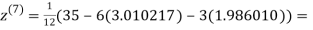 0.915055
0.915055
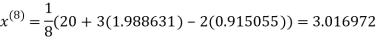
 1.986532
1.986532
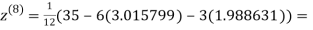 0.911609
0.911609

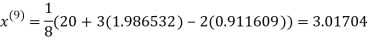
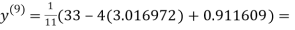 1.985792
1.985792
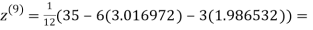 0.911547
0.911547
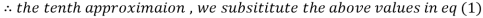
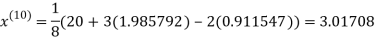
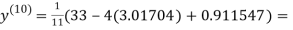 1.98576
1.98576
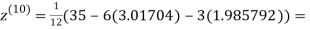 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 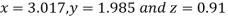
5. Solve by Jacobi’s Method, the equations
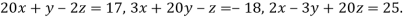
Given equation can be rewrite in the form
 … (i)
… (i)
 ..(ii)
..(ii)
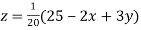 ..(iii)
..(iii)
Let the initial approximation be 

Putting these values on the right of the equation (i), (ii) and (iii) and so we get
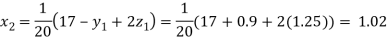
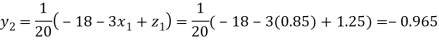

Putting these values on the right of the equation (i), (ii) and (iii) and so we get

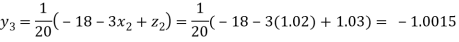

Putting these values on the right of the equation (i), (ii) and (iii) and so we get
 0.90025
0.90025
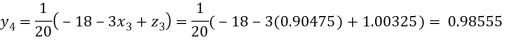

Putting these values on the right of the equation (i), (ii) and (iii) and so we get
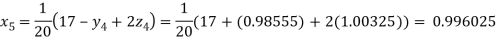


Putting these values on the right of the equation (i), (ii) and (iii) and so we get
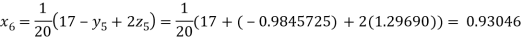
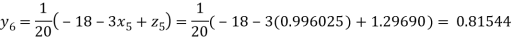

Hence solution approximately is 
6. Use Jacobi’s method to solve the system of the equations
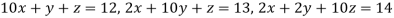
Rewrite the given equations


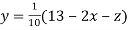 (1)
(1)

Let the initial approximation be 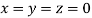
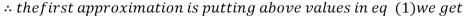
 1.2
1.2
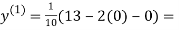 1.3
1.3
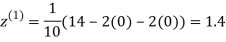


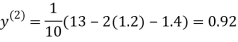
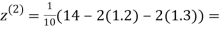 0.9
0.9
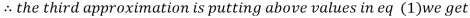

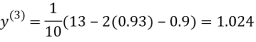
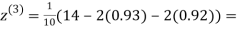 1.03
1.03
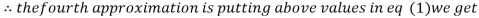
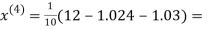 0.9946
0.9946
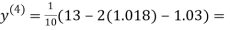 0.9934
0.9934
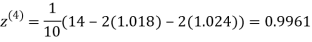
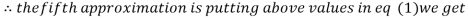
 1.0015
1.0015
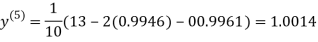
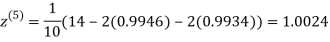
Hence the solution of the above equation correct to two decimal places is
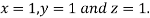
7. Use Gauss –Seidel Iteration method to solve the system of equations
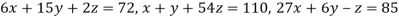
Since 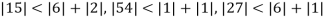
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations

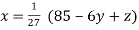
 (1)
(1)
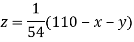
Let the initial approximation be 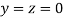
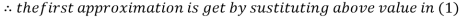
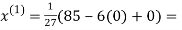 3.14814
3.14814
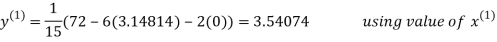
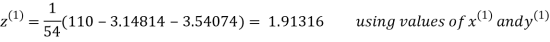
 2.43217
2.43217

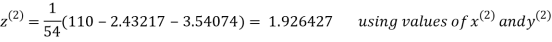
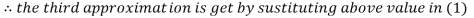
 2.42571
2.42571



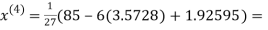 2.4260
2.4260

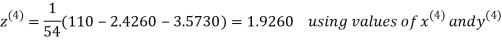
Hence the solution correct to three decimal places is
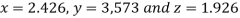
8. Solve the following system of equations
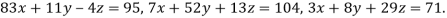
By Gauss-Seidel method.
Rewrite the given system of equations as
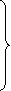

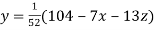 (1)
(1)
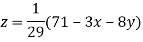
Le t the initial approximation be 

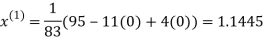
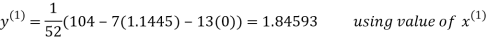
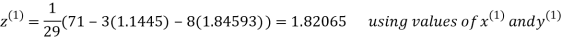
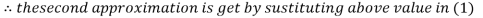
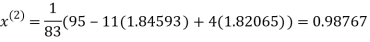


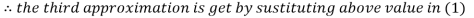
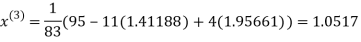

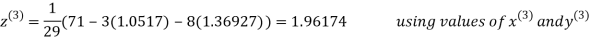
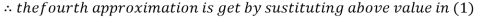

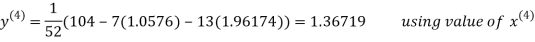

Thus the required solution is 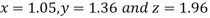
9. Solve the following equations by Gauss-Seidel Method
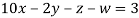

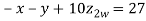
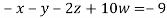
Rewrite the above system of equations
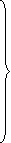
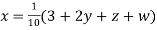

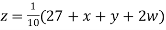 (1)
(1)
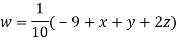
Let the initial approximation be 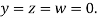
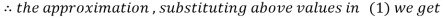
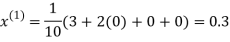
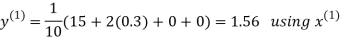

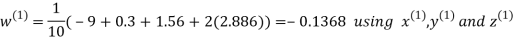

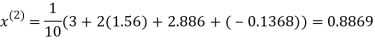




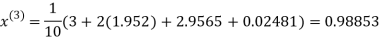
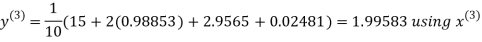

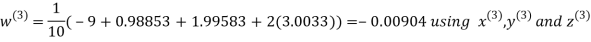
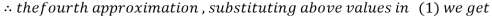
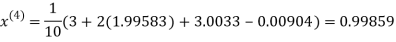
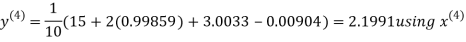
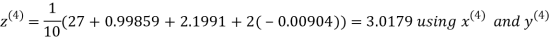

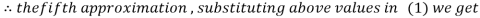
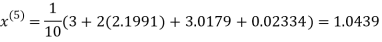
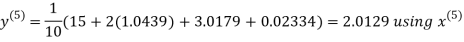
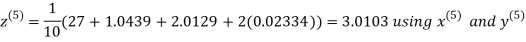
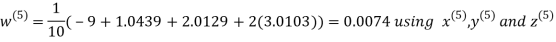
Hence the required solution is 