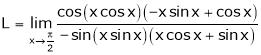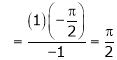Unit - 5
Expansion of Functions and Indeterminate forms
Question and answer
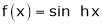 Then
Then

Proof:-
Here f(x) = sin hx.
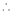 By Maclaurin’s expansion,
By Maclaurin’s expansion,
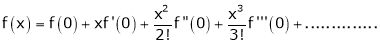 (1)
(1)

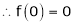

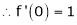

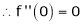

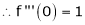
 By equation (1) we get,
By equation (1) we get,
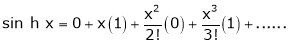
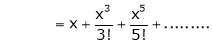
2. 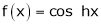 . Then
. Then
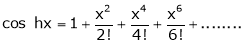
Proof:-
Here f(x) = cos hx
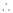 By Maclaurin’s expansion
By Maclaurin’s expansion
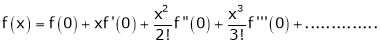 (1)
(1)
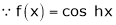

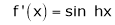



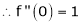
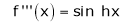

 By equation (1)
By equation (1)
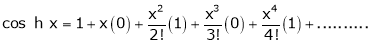
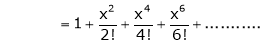
3. f(x) = tan hx
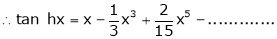
Proof:
Here f(x) = tan hx
 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
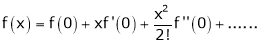 … (1)
… (1)
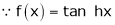
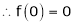
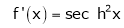


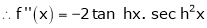
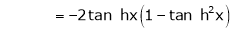

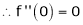
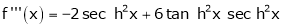
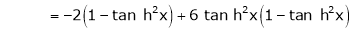
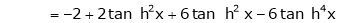
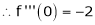

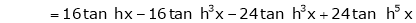
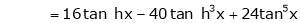

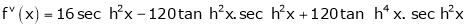

 By equation (1)
By equation (1)
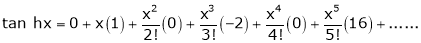
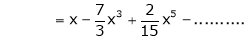
4. 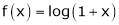 then
then

Proof:-
Here f(x) = log (1 + x)
 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
 … (1)
… (1)

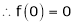

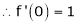
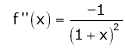
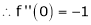

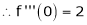
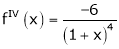

 By equation (1)
By equation (1)
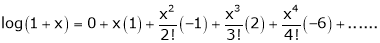
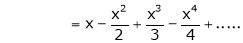
5. 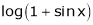
Solution:
Here f(x) = log (1 + sin x)
 By Maclaurin’s Theorem,
By Maclaurin’s Theorem,
 … (1)
… (1)


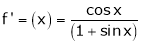
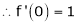
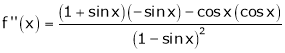
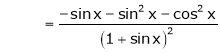
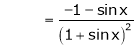
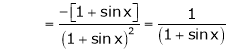

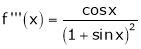
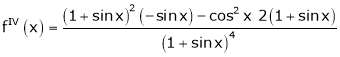
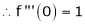
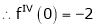 ……..
……..
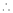 equation (1) becomes,
equation (1) becomes,
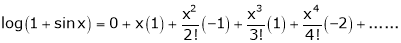
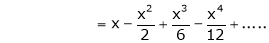
6. Expand 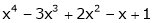 in power of (x – 3)
in power of (x – 3)
Solution:
Let 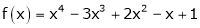
Here a = 3
Now by Taylor’s series expansion,
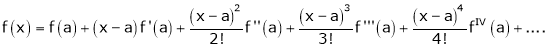 … (1)
… (1)
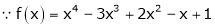
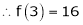
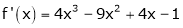
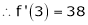
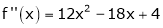
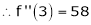
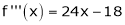
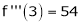
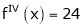
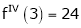
 equation (1) becomes.
equation (1) becomes.
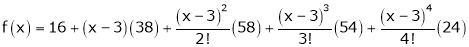

7. Using Taylors series method expand
 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 
a = -2
 By Taylors series,
By Taylors series,
 … (1)
… (1)
Since
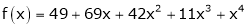

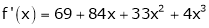
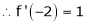
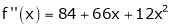

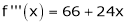
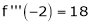
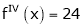
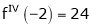 ,
, , …..
, …..
Thus equation (1) becomes
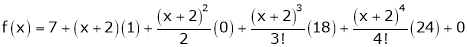
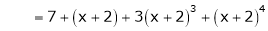
8. Expand 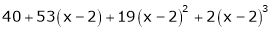 in ascending powers of x.
in ascending powers of x.
Solution:
Here
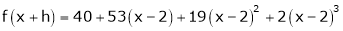
i.e. 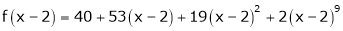
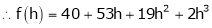
Here h = -2
 By Taylors series,
By Taylors series,
 … (1)
… (1)
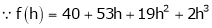
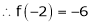
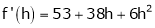
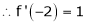
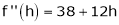
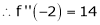
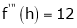
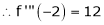

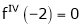
 equation (1) becomes,
equation (1) becomes,
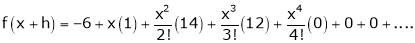

Thus
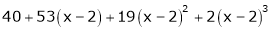
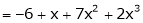
9. Expand 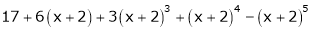 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
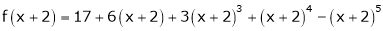
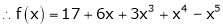
i.e. 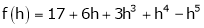
Here
h = 2
 By Taylors series
By Taylors series
 … (1)
… (1)
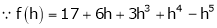
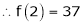
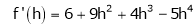
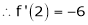
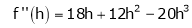



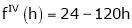
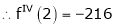
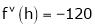
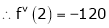
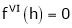
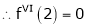
 By equation (1)
By equation (1)
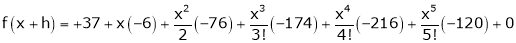
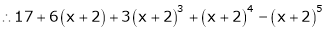
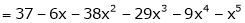
10. Evaluate 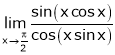
Solution:
Let
 …
… 
 By L – Hospital rule
By L – Hospital rule