| unit 2 gradually varied flow gvf

FM 2

UNIT-2GRADUALLY VARIED FLOW (GVF) Q1) What do you mean by gradually varied flow? State the assumptions.A1) A steady non-uniform flow in a prismatic channel with gradual changes in its water surface elevation is named gradually-varied flow (GVF). The backwater produced by a dam or weir across a river and drawdown produced at a sudden drop in a channel is few typical examples of GVF. In a GVF, the velocity varies along the channel, and consequently, the bed slope, water surface slope, and energy line slope will all differ from each other. Regions of high curvature are excluded in the analysis of this flow.The two basic assumptions involved in the analysis of GVF are 1. The pressure distribution at any section is assumed to be hydrostatic. This follows from the definition of the flow to have a gradually varied water surface. As gradual changes in the surface curvature give rise to negligible normal accelerations, the departure from the hydrostatic pressure distribution is negligible.2. The resistance to flow at any depth is assumed to be given by the corresponding uniform flow equation, such as the Manning equation, with the condition that the slope term to be used in the equation is the energy line slope, Se and not the bed slope, S0. Thus, if in a GVF the depth of flow at any section is y, the energy line slope Se is given by,

where R = hydraulic radius of the section at depth y.

Q2) Derive the expression for Specific Energy.A2) In open channel flow, specific energy (e) is the energy length, or head, relative to the channel bottom. Specific energy is expressed in terms of kinetic energy, and potential energy, and internal energy. The Bernoulli equation, which originates from a control volume analysis, is used to describe specific energy relationships in fluid dynamics. The form of Bernoulli’s equation discussed here assumes the flow is incompressible and steady.The three energy components in Bernoulli's equation are elevation, pressure, and velocity. However, since with open channel flow, the water surface is open to the atmosphere, the pressure term between two points has the same value and is therefore ignored. Thus, if the specific energy and the velocity of the flow in the channel are known, the depth of flow can be determined. This relationship can be used to calculate changes in depth upstream or downstream of changes in the channel such as steps, constrictions, or control structures. It is also the fundamental relationship used in the standard step method to calculate how the depth of a flow changes over a reach from the energy gained or lost due to the slope of the channel.With the pressure term neglected, energy exists in two forms, potential and kinetic. Assuming all the fluid particles are moving at the same velocity, the general expression for kinetic energy applies (KE = ½mv2). This general expression can be written in terms of kinetic energy per unit weight of the fluid,

Where: m= mass,v= Fluid velocity (length/time),V= Volume (length3),ρ= Fluid density (mass/volume),γ= Specific weight of water (weight/unit volume),g= Acceleration due to gravity (length/time2)
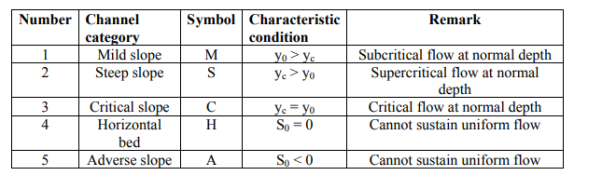
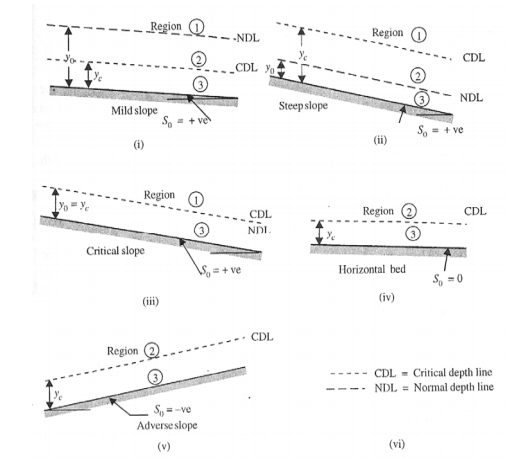
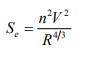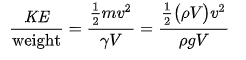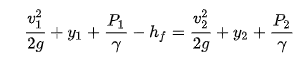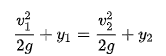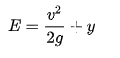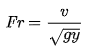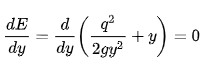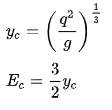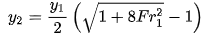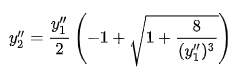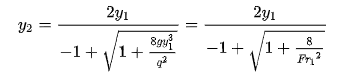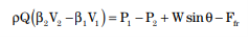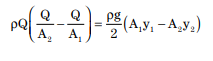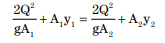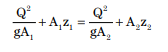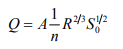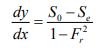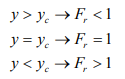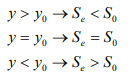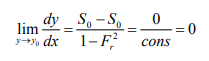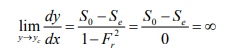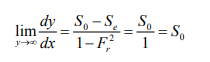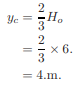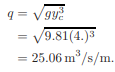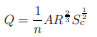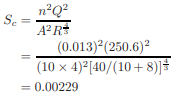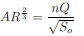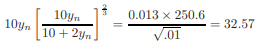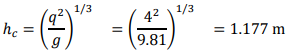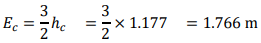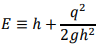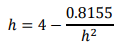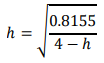The kinetic energy, in feet, is represented as the velocity head,

The fluid particles also have potential energy, which is associated with the fluid elevation above an arbitrary datum. For a fluid of weight (ρg) at a height y above the established datum, the potential energy is wy. Thus, the potential energy per unit weight of fluid can be expressed as simply the height above the datum, {\displaystyle {\frac {\mathit {PE}}{\rho g}}=y}

Combining the energy terms for kinetic and potential energies along with influences due to pressure and headloss results in the following equation:

Where, y = the vertical distance from the datum (length), P = pressure (weight/volume),hf = headloss due to friction (length)As the fluid moves downstream, energy is lost due to friction. These losses can be due to channel bed roughness, channel constrictions, and other flow structures. Energy loss due to friction is neglected in this analysis.The previous equation evaluates the flow at two locations: point 1 (upstream) and point 2 (downstream). As mentioned previously, the pressure at locations 1 and 2 both equal atmospheric pressure in open-channel flow, therefore the pressure terms cancel out. Head loss due to friction is also neglected when determining specific energy; therefore, this term disappears as well. After these cancelations, the equation becomes,

{\displaystyle {\frac {v_{1}^{2}}{2g}}+y_{1}={\frac {v_{2}^{2}}{2g}}+y_{2}}

and the total specific energy at any point in the system is,

Q3) Describe Specific Energy diagram,A3) For a given discharge, the specific energy can be calculated for various flow depths and plotted on an E–y diagram. A typical E–y diagram is shown below.

E–Y Diagram

Three different q values are plotted on the specific energy diagram above. The unit discharges increase from left to right, meaning that q1 < q2 < q3. There is a distinct asymptotic relationship as the top part of the curve approaches the E = y line and the bottom part of the curve tends toward the x-axis. Also shown are the critical energy or minimum energy, Ec, and the corresponding critical depth value, yc. The values shown are for the q1 discharge only, but unique critical values exist for any discharge. Q4) What is a critical flow relationship?

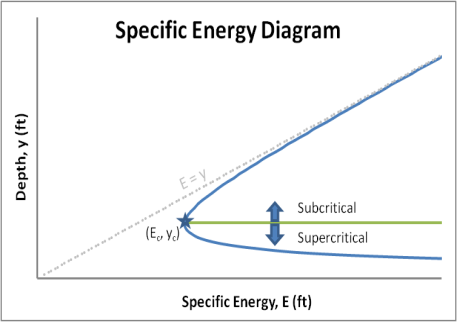
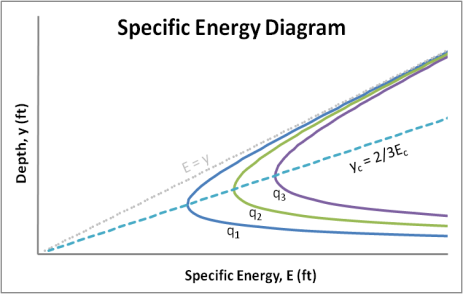
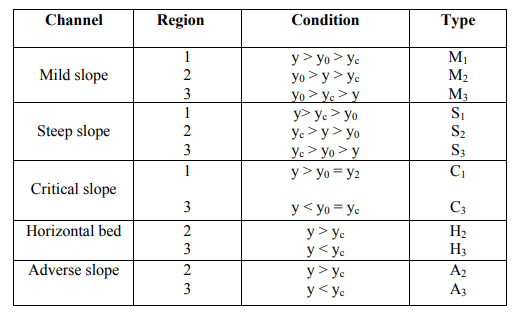
A4) The critical depth value mentioned in the E–y diagram section above is mathematically represented by the ratio of the fluid velocity to the velocity of a small amplitude gravity wave. This ratio is called the Froude number.

The critical depth has a Froude number equal to one and corresponds to the minimum energy a flow can possess for a given discharge. Not all flows are critical. Froude numbers below one are considered subcritical and Froude numbers above one are considered supercritical.Fr{\displaystyle {\mathit {Fr}}=1;\;{\textit {Critical}}}=1; Critical Fr{\displaystyle {\mathit {Fr}}=1;\;{\textit {Critical}}}<1; Subcritical{\displaystyle {\mathit {Fr}}<1;\;{\textit {Subcritical}}} {\displaystyle {\mathit {Fr}}>1;\;{\textit {Supercritical}}}Fr{\displaystyle {\mathit {Fr}}=1;\;{\textit {Critical}}}>>>1; Supercritical Physically, subcritical flow is deep and the velocities are slow. This means subcritical flow has high potential energy and low kinetic energy. Supercritical flow on the other hand tends to be shallow and the velocities are fast. Supercritical flow has low potential energy and high kinetic energy.If we refer back to the basic E–y diagram, it is seen that a line passes through the critical value on each successive discharge curve. This line corresponds to {\displaystyle y=2/3E}y=2/3E.

Depth values on the E–y curve greater than the critical depth correspond to subcritical flow depths. Likewise, values less than the critical depth correspond to supercritical flow depths.For rectangular channels, the critical depth can be calculated by taking the derivative of the energy equation and setting it equal to zero. The energy associated with the critical depth is found by placing the critical depth expression into the specific energy equation. The critical energy expression is demonstrated graphically by the line {\displaystyle y_{c}=2/3E_{c}}yc=2/3Ec, which connects critical depth values.

Q5) Derive the Alternate depth equation.

A5) Using the conjugate depth equation and the duality concept between the dimensionless forms of the momentum (M') and specific energy (E") functions an analytical relationship between alternate depths can be obtained.

1) Start with the conjugate depth equation

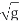, where Fr1 is the Froude number at location 12) Develop the analog to Fr1 by observing that the dimensionless momentum equation. It has a value of y' equal to unity at critical depth. If we chose q=

then the resulting M-y relationship will be numerically identical to the dimensionless M'-y' relationship since yc is unity. For this unit discharge q, the Froude number simplifies to:

3) Although dimensionally y1 and y1" are different, their numerical magnitudes are the same at unity and thus we can express the analog of the Fr1 in the conjugate depth equation as:

where the tilde in the {\displaystyle {\tilde {{\mathit {Fr}}_{1}}}}Fˉr1 symbol indicates that this is simply the specific-energy equation analog to the Froude number in this analysis.4) Substituting {\displaystyle {\tilde {{\mathit {Fr}}_{1}}}}Fr1 into the dimensionless conjugate depth equation and recalling {\displaystyle y''={\frac {1}{y'}}={\frac {y_{c}}{y}}}y”=1/y’= yc/y for both y1 and y2:

5) Observing that y2= yc/y2” and (y1”)3= (yc/y1)3=q2/gy13, equation (2.27) can be simplified to the final analytical alternate depth relationship:

6) Recalling that for rectangular channels, yc=(q2/g)1/3 and Fr= v/

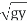= q/y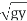

and recognizing that Fr2= (yc/y)3= q2/gy3, the final analytical alternative depth relationship can also be represented as: {\displaystyle y_{c}=\left({\frac {q^{2}}{g}}\right)^{\frac {1}{3}}}{\displaystyle y_{2}={\frac {y_{c}}{y_{2}''}}}

Notice that because of the symmetry of the original conjugate depth equation, the resulting dimensionless alternate depth equation applies regardless of the Froude number at location 1. That is, y1 may correspond to either supercritical or subcritical flow conditions. The alternate depth relationship will yield the alternate depth to y1 corresponding to the opposite flow regime in either case. Q6) Define specific force and derive the momentum equation.A6) Specific force is the horizontal force of flowing water per unit weight of water. It is derived from the momentum equation. A specific force curve looks similar to the specific energy curve. The critical depth occurs both at the minimum energy for a given discharge and also at the minimum specific force for a given discharge. This similarity shows how energy concepts and force or momentum concepts can be employed similarly in many hydraulic analyses, often with nearly identical results. The designer should know what circumstances would cause the two approaches to diverge, however. Specific force concepts are applied over short horizontal reaches of the channel, where the difference in external friction forces and force due to the weight of water are negligible. Examples are the flow over a broad-crested weir through a hydraulic jump or at junctions. One way to conceptualize why a momentum-based method, rather than an energy-based method, might be more applicable would be to energy changes in a hydraulic jump. Much energy is lost through the turbulence caused by moving mass colliding with other mass that is not accounted for by energy principles alone. An equation for specific force may be derived from the momentum equation. The momentum equation may be written as:

If one wishes to apply this equation to short sections of the channel such as a weir or hydraulic jump, the frictional resistance forces, Ffr can be neglected. With a flat channel of low slope, θ approaches 0, then the last two terms in equation 2.18 can be dropped. As a result, equation 2.18 becomes:ρQ(β2V2- β1V1)= P1-P2 Assume also that the Boussinesq coefficient (β) is 1. From the fact that the pressure increases with depth to the maximum of ρgy at the channel bottom (y being depth, b being channel width, and ρ being fluid density), the overall pressure on the vertical flow area may be expressed as 1/2ρgby2. The velocities may be expressed as Q/A. For a rectangular channel:

that becomes:

For a channel section of any other shape, the resultant pressure may be taken at the centroid of the flow area, at a depth, z, from the surface. Then the momentum formulation is:

Either side of this equation is the definition of specific force, and the specific force is constant over a short stretch of the channel such as a hydraulic jump. The first term represents the change in momentum over time, and the second term the force of the water mass. As Chow (1959) explains, specific force is sometimes called force plus momentum or momentum flux.

Image result for specific force in open channel flow

Momentum equation and Specific Force Q7) Give classification of water surface profiles.A7) For a given channel with a known Q = Discharge, n = Manning coefficient, and S0 = Channel bed slope, yc = critical water depth and y0 = Uniform flow depth can be computed. There are three possible relations between y0 and yc as 1) y0 > yc ,2) y0 < yc , 3) y0 = yc . For horizontal (S0 = 0), and adverse slope ( S0 < 0) channels,

Horizontal channel, S0 = 0→ Q = 0,The adverse channel, S0 < 0, Q cannot be computed,For horizontal and adverse slope channels, uniform flow depth y0 does not exist. Based on the information given above, the channels are classified into five categories as indicated in the table below

Classification of channelsFor each of the five categories of channels, lines representing the critical depth (yc) and normal depth (y0 ) (if it exists) can be drawn in the longitudinal section. These would divide the whole flow space into three regions: Region 1: Space above the topmost line, Region 2: Space between the top line and the next lower line, Region 3: Space between the second line and the bed.The figure shows these regions in the various categories of channels.

Fig. 2-8 Regions of flow profilesDepending upon the channel category and region of flow, the water surface profiles will have characteristic shapes. Whether a given GVF profile will have an increasing or decreasing water depth in the direction of flow will depend upon the term dy/dx is positive or negative

For a given Q, n, and S0 at a channel, y0 = Uniform flow depth, yc = Critical flow depth, y = Non-uniform flow depth. The depth y is measured vertically from the channel bottom, the slope of the water surface dy/dx is relative to this channel bottom.

Fig. 2-9To assist in the determination of flow profiles in various regions, the behavior of dy/dx at certain key depths is noted:

And also,

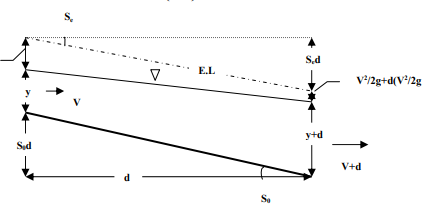
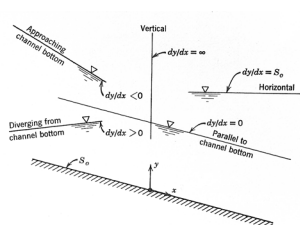
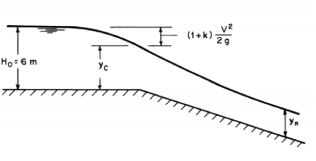
1. As y → y0, V →V0, Se = S0

The water surface approaches the normal depth asymptotically

2. As y → yc, Fr 2 =1, 1 − Fr2 = 0,

3. As y → ∞ , V= 0→ Fr = 0→ Se→0

The water surface meets a very large depth as a horizontal asymptote. Based on this information, the various possible gradually varied flow profiles are grouped into twelve types

Gradually Varied Flow profiles Q8) A 10-m wide, rectangular, concrete-lined channel (n = 0.013) has a bottom slope of 0.01 and a constant-level reservoir at the upstream end. The reservoir water level is 6.0 m above the channel bottom at the entrance. Assuming the entrance losses and the approach velocity in the reservoir to be negligible, determine the channel discharge and qualitatively sketch the water surface profile. A8) Given: n = 0.013 S0 = 0.01 B = 10.0 m H0= 6.0 m Entrance losses are negligible Determine: Q = ? Water-surface profile. Solution: Let us assume the control is at the channel entrance, i.e., the bottom slope is steep or critical. Then,

For critical flow, unit discharge,

Hence,Q = Bq = 10 × 25.06 = 250.6 m3/sLet us now determine the critical slope, Sc. This is the bottom slope for which we will have critical flow in the channel for Q = 250.6 m3/s. Now, the Manning equation may be written as

Since, Sc < So, the slope of the channel bottom is steep and the channel discharge is 250.6 m3/s. To sketch the water-surface profile, we first determine the normal depth. The flow area, A, and the hydraulic radius, R, corresponding to the normal depth satisfy the following equation

The substitution of the values of n, Q, and So and the expressions for A and R in terms of yn into this equation gives

The solution of this equation by trial and error yields yn = 2.37m The entrance flow depth will be critical and it will approach the normal depth asymptotically, as shown in Fig.

Q9) A trapezoidal channel having a bottom slope of 0.001 is carrying a flow of 30 m3/s. The bottom width is 10.0 m and the side slopes are 2H to 1V. A control structure is built at the downstream end which raises the water depth at the downstream end to 5.0 m. The normal depth is 1.16m. Compute the water surface profile. Manning n for the flow surfaces is 0.013 and α = 1. A9) Given: Bottom slope, S0 = 0.001 Discharge, Q = 30 m3/s Channel width, B0 = 10.0 m Manning n = 0.013 yn= 1.16mDepth at the downstream end (i.e., at x = 0) = 5.0 m α = 1 Determine Water-surface profile in the channel. Solution: The normal depth, yn, for this channel is given as 1.16 m. The flow depth approaches the normal depth asymptotically at an infinite distance. Therefore, the computation of the surface profile may be stopped when the flow depth is within about five percent of the normal depth. We will continue the calculations until y = 1.05yn = 1.05 × 1.16 = 1.21, say 1.20 m. We start the computations with a known depth of 5.0 m at the control structure and proceed in the upstream direction. Let us call the location at the control structure as x = 0. Since we are considering the distance in the downstream flow direction as positive, the values of x we determine are negative. The calculations are done systematically as shown in the table. Here, the depth for the step under consideration is the current depth and the depth for the previous step as the previous depth. Column 1, y We first use large increments of change in y, i.e., 0.5 m, and then decrease their size, i.e., 0.1 m, as the rate of variation of y with x becomes small. Column 2, A This is the flow area for the depth of column 1. Column 3, R Hydraulic radius, R = A/P, where P = wetted perimeter for the flow depth of column 1. Column 4, V Flow velocity, V is computed by dividing the specified rate of discharge, Q, by the flow area, A, of column 2. Column 5, Sf By using the specified value of Manning n, and the computed values of V of column 4 and R of column 3, this column is computed from the equation,

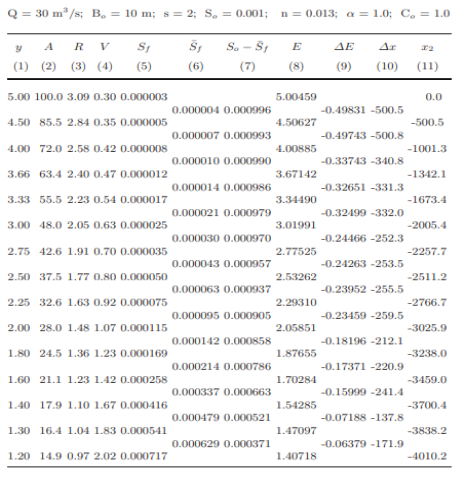
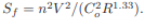Column 6, Sfˉ This is the average of Sf for the current depth and the previous depth. This column is left blank for the first line since there is no previous depth when we start the computations. To indicate that this is an average slope, we list it between the lines corresponding to the current and the previous depths. Column 7, So − Sf¯ This is obtained by subtracting the Sf¯ of column 6 from the specified value of S0. Column 8, E The specific energy, E, is computed for the selected value of y of column 1 and the corresponding computed value of V of column 4, i.e., E = y + αV2/(2g). Column 9, ΔE = E2 − E1 This column is obtained by subtracting E for the current depth from E for the previous depth. Again, since this column is the difference of E values corresponding to the current and the previous depths, we list its value between the lines for these depths. Column 10, Δx = x2 − x1 The distance increment is computed from the equation, Δx = (E2−E1)/(S0− Sf¯), i.e., dividing column 9 by column 7. Column 11, x2 This is the distance where depth y will occur. It is obtained by algebraically adding Δx of column 10 to the x2 value for the previous depth.

Q10) A 3-m wide channel carries a total discharge of 12 m3/s. Calculate: (a) the critical depth; (b) the minimum specific energy; (c) the alternate depths when 𝐸 = 4 m.A10)

𝑏 = 3 m 𝑄 = 12 m3/s

(a) Discharge per unit width:

𝑞 = 𝑄/𝑏 = 12/3 = 4 m2/s

Then, for a rectangular channel: