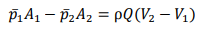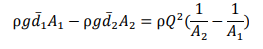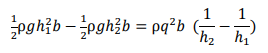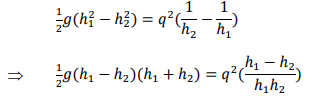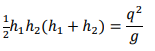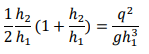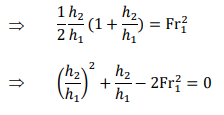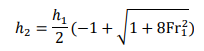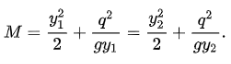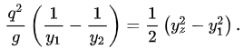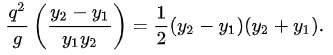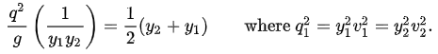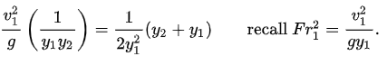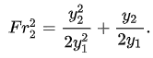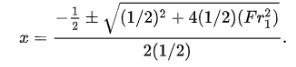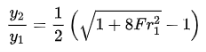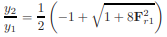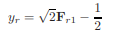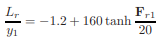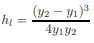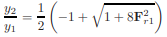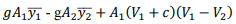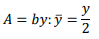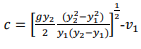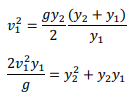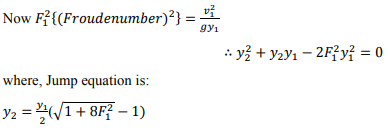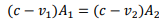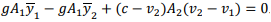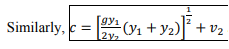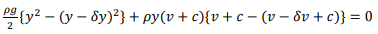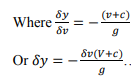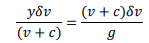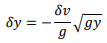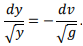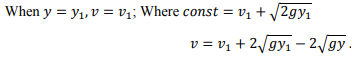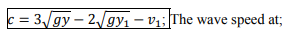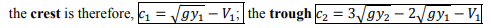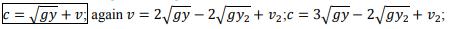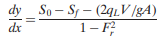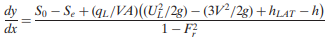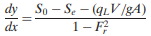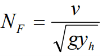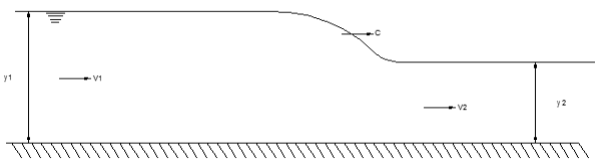
undefined | unit 3 rapidly varied flow rvf

FM 2

UNIT-3RAPIDLY VARIED FLOW Q1) What is a Hydraulic jump? Derive continuity momentum equation. A1) A hydraulic jump is an abrupt change from a shallow, high-speed flow to a deep, low-speed flow of lower energy.

Hydraulic Jump It occurs when a depth difference is imposed by upstream and downstream conditions. Rapid, shallow flow may be created by, for example, a steep spillway or sluice. A slower and deeper downstream flow may be controlled by a downstream weir or by a reduction in slope.The volume flow rate 𝑄 = 𝑉𝐴 is the same at each section. Velocities can thus be related to cross-sectional area 𝐴 (and hence to depth) by V= Q/A

Consider a control volume encompassing the jump. By the momentum principle: net pressure force = rate of change of momentum

Since streamlines are parallel there, pressures at inflow and outflow stations 1 and 2 are hydrostatic and the average pressure is the pressure at the centroid; i.e. 𝑝̅= ρ𝑔𝑑̅, where 𝑑̅is the depth of the centroid below the surface. Using this, and substituting for velocity,

At this point, we restrict ourselves to a rectangular or wide channel (but, for different shapes, see the Examples). With 𝑏 the width of the channel (or 𝑏 = 1 unit for a “wide” channel):

𝑑̅= 1 /2 ℎ, 𝐴 = ℎ𝑏, 𝑄 = 𝑞𝑏

and the momentum principle reduces to

Dividing by ρ𝑏:

Divide through by 𝑔(ℎ1 − ℎ2) (non-zero by assumption) and then multiply by ℎ1ℎ2:

Since we are looking for the depth ratio ℎ2⁄ℎ1, divide through by ℎ1 3 :

Since 𝑞 = 𝑉ℎ, the RHS is 𝑉12 /𝑔ℎ1 or Fr12. Hence,

This is a quadratic equation for the depth ratio ℎ2⁄ℎ1 and its positive root gives the downstream depth in terms of upstream quantities:

Q2) Describe conjugate depth and derive its mathematical formula.A2) In fluid dynamics, the conjugate depths refer to the depth (y1) upstream and the depth (y2) downstream of the hydraulic jump whose momentum fluxes are equal for a given discharge (volume flux) q. The depth upstream of a hydraulic jump is always supercritical. It is important to note that the conjugate depth is different from the alternate depths for the flow which are used in energy conservation calculations. Mathematical derivation

M–y diagram.

Beginning with an equal momentum flux M and discharge q upstream and downstream of the hydraulic jump:

Rearranging terms gives:

Multiply to get a common denominator on the left-hand side and factor the right-hand side:

The (y2−y1) term cancels out:

Divide by y12

Thereafter multiply by y2 and expand the right-hand side:

Substitute x for the constant y2/y1:

Solving the quadratic equation and multiplying it by √4/2 gives:

Substitute the constant y2/y1 back in for x to get the conjugate depth equation

Q3) State characteristics of hydraulic jump.A3) Some major characteristics of a hydraulic jump are as follows:1. The ratio of Sequent Depths

The above Equation relates the flow depths on the upstream and downstream sides of a classical jump in terms of the Froude number at the entrance to the jump, Fr1. Let's say Fr1 is the approach Froude number. From this equation, it can be proved that for Fr1 > 2,

2. Length of Jump The length of a jump is needed to select the apron length and the height of the sidewalls of a stilling basin. To determine the length of a jump during laboratory investigations, it is difficult to mark the beginning and the end of a jump because of the highly turbulent flow surface, the formation of roller and eddies, and air entrainment. Besides, the surface disturbances are random, and the time-averaged quantities may not always give consistent results. The length of the roller may be taken to the point where the flow velocity at the top reverses and the jet continues. The following equation for the length of the roller, Lr gives good results if y1/B < 0.1

3. Jump Profile The information on the jump profile is needed to determine the weight of water in a dissipator to counteract the uplift force if the basin floor is laid on a permeable foundation. Also, the height of the sidewalls may be varied for economic reasons if the water profile is known. An empirical relationship for the flow depth, y, at a distance, x, from the beginning of the jump is given byY = tanh(1.5x) 4. Jump types The hydraulic jump occurs in four distinct forms [Peterka, 1958] depending upon the approach Froude number, Fr1, as shown in Figure 3-6. Each of these forms has a distinct flow pattern, formation of rollers and eddies, etc.

Weak jump ( 1 < Fr1 < 2.5)

For 1 < Fr1 < 1.7, y1 and y2 are approximately equal to each other and only a slight ruffle is formed on the surfaceii. Oscillating jump (2.5 < Fr1 < 4.5) The jet at the entrance to the jump oscillates from the bottom to the top at an irregular period. Turbulence may be near the channel bottom at one instant and the water surface at the next.iii. Steady jump (4.5 < Fr1 < 9) For this range, the jump forms steadily at the same location, and the position of the jump is least sensitive to the downstream flow conditionsiv. Strong jump (Fr1 > 9) In this case, the difference between the conjugate depths is large. At irregular intervals, slugs of water roll down the front of the jump face into a high-velocity jet and generate additional waves. 5. Energy lossThe difference between the total head upstream and downstream of the jump is the energy loss in the jump which is given by:

This is a theoretical expression for the head losses in a classical jump. 6. Jump Location A hydraulic jump is formed at a location where the flow depths upstream and downstream of the jump satisfy the equation for the sequent depth ratio. The jump is formed on the apron if the downstream depth, yd, is equal to the depth y2

given by. 7. Control of Jump The location of a jump may be controlled by providing several appurtenances, such as baffle blocks, sill, drop or rise in the channel bottom. Q4) What are the applications of a hydraulic jump?A4) Applications for hydraulic jumps

The hydraulic jump is the most commonly used choice of design engineers for energy dissipation below spillways and outlets. A properly designed hydraulic jump can provide for 60-70% energy dissipation of the energy in the basin itself, limiting the damage to structures and the streambed. Even with such efficient energy dissipation, stilling basins must be carefully designed to avoid serious damage due to uplift, vibration, cavitation, and abrasion. An extensive literature has been developed for this type of engineering.

While traveling down the river, kayaking, and canoeing paddlers will often stop and playboat in standing waves and hydraulic jumps. The standing waves and shock fronts of hydraulic jumps make for popular locations for such recreation.

Similarly, kayakers and surfers have been known to ride bores up rivers.

Usually, a hydraulic jump reverses the flow of water. This phenomenon can be used to mix chemicals for water purification.

Hydraulic jump usually maintains the high water level on the downstream side. The water level can be used for irrigation purposes.

The hydraulic jump can be used to remove the air from the water supply and sewage lines to prevent the air locking.

Q5) Describe a surge in an open channel.

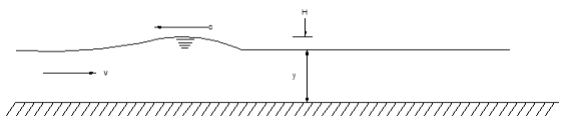
A5) The sudden changes of flow in the open channel result in the increase or decrease of flow depth are called the "surge" in an open channel. This could take place when there is a breaching of dams due to earthquakes or regulating the hydropower sluice gates. Hence results in positive and negative surges in the downstream river channel or the downstream tail channel of hydropower projects. This phenomenon also governs when there would be flood (unsteady flow) during the monsoon period in natural river channels and the hydrograph significantly varies with rising and falling as the rainfall takes its peak period. The flood wave generates during the positive or negative surges is called the celerity (wave velocity) of the flood in an unsteady flow situation.

This positive or negative surge sometimes travels downstream or upstream depending on the situation. The increase in flow depth would become the crest of the surges and the decrease in the flow depth would become the trough of the surges.

Propagation of low wave in channel The celerity or speed of propagation relative to the water is given by √gy where y is the water depth. Therefore, the velocity of the wave relative to a stationary observer is:c= √gy+-v This can be noted that the Froude number Fr expressed by v/√gy is the ratio of water velocity to wave celerity. If the Froude number is greater than unity, which corresponds with the supercritical flow, a small gravity wave cannot be propagated upstream. Waves of finite height are dealt with in a section of open channel surges. A surge is produced in the channel by a rapid change in the rate of flow, for example, by the rapid opening or closure of sluice gates of the project. The former causes a positive surge wave to move downstream (Fig. a) and the latter produces a positive surge wave that moves upstream. (Fig.b)

Positive surge wavesA stationary observer, therefore, sees an increase in depth as the wavefront of a positive surge wave passes. A negative surge wave, on the other hand, leaves a shallower depth as the wavefront passes.

Negative Surge Waves

Q6) Derive upstream and downstream positive surge formula.

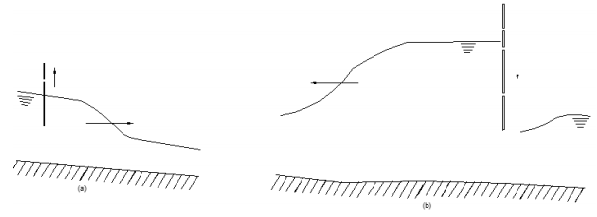
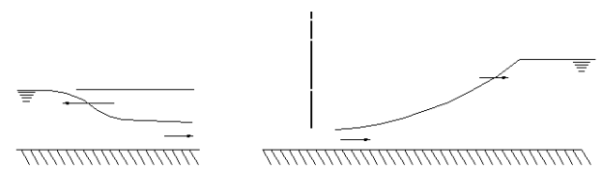
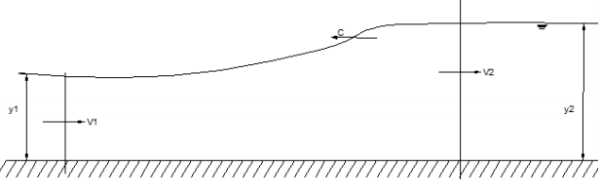
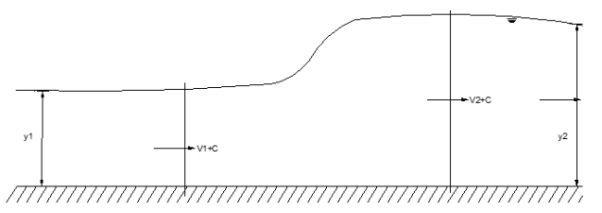
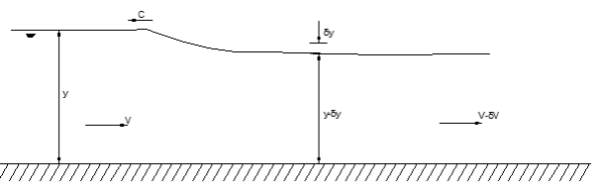
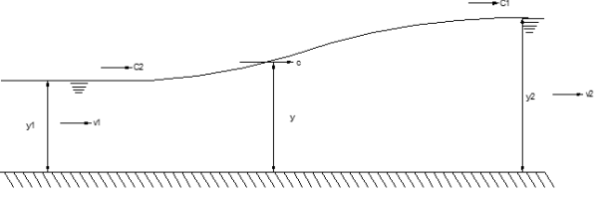
A6) The upstream positive surge wave Consider the propagation of a positive wave upstream in a frictionless channel resulting from gate closure

Upstream Positive SurgesThe front of the surge wave is propagated upstream at celerity, c, relative to the stationary observer. To the observer, the flow situation is unsteady as a wavefront passes; to an observer traveling at a speed, c, with the wave the flow appears steady although non-uniform. The following fig shows the surge reduced to a steady-state.

The continuity equation is:

A1(V1+c)= A2(V2+c)

The momentum equation is:

Where y1ˉ and y2ˉ are respective depths of the centers of the area. From simplification, we get

In the special case of the rectangular channel,

From the above equation, it can be written as

then;

The hydraulic jump in a stationary surge. Putting c=0, in the above equation

In the case of a low wave where y2 approaches y1 then the equation becomes

Then c=√gy=v1

And in still water (v1=0)

c=√gy

The downstream positive surge This type of wave may occur in the channel downstream from a slice gate at which the opening is rapidly increased.

Downstream Positive Surges

Reducing the flow to steady-state. From continuity equation:

Momentum:

Q7) Describe negative upstream and downstream surgeA7) Negative Surge Waves The negative surge wave appears to a stationary observer as a lowering of the liquid surface. Such wave occurs in the channel downstream from the control gate the opening of which is rapidly reduced or in the upstream channel as the gate is opened. The wavefront can be considered to be composed of a series of small waves superimposed on each other. Since the uppermost wave has the greatest depth it travels faster than those beneath; the retreating wavefront, therefore, becomes flatter. As shown in fig below

Propagation of Negative SurgesThe figure shows a small disturbance in a rectangular channel caused by a reduction in downstream discharge; the wave propagates upstream as described below:

Neglecting the product of small quantities

The momentum equation is

Equating the above equations;

Where C=√gy=v

Substituting for (v +c) from above equations;

And in the limit as ∂y→ 0

For a wave of finite height, integration of the above equation yields

V=-√2gy+constant

Negative surges of finite height

From equation c=√gy=v and substituting in the above equation then it becomes;

In the case of a downstream negative surge in a frictionless channel as shown below a similar approach yields;

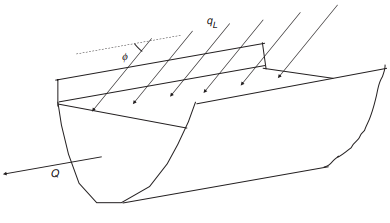
Downstream negative surges Q8) What is spatially varied flow? Derive its equation.A8) Flow in an open channel is said to be spatially varied if there is lateral flow into (or out of) the channel, as shown schematically in Figure. For steady spatially-varied flow, the continuity equation becomes dQ/dx= qL

Definition sketch for spatially-varied flowwhere qL= lateral inflow rate per unit length of the channel. Note that the dimension of qL is {length}2 /{time}.

As demonstrated by Yen and Wenzel (1970), for β=1, the momentum equation for steady spatially-varied flow can be written as

where UL = velocity of lateral flow and ø is the angle between the lateral flow and channel flow directions. If lateral flow joins (or leaves) the channel in a direction perpendicular to the main flow direction, the equation becomes

Yen and Wenzel (1970) also demonstrated that, for α=1, the energy equation can be written as

where h= zb+y = piezo metric head of the main channel flow, and hLAT = piezo metric head of the lateral inflow. If h = hLAT, and V = UL, last equation is simplified to obtain

Q9) Q = 18m3 /s, Rectangular channel = 3m wide Channel – unfinished form concrete Hydraulic jump occurs where the depth is 1m = y1. Determine Velocity before the jump, Depth after jump, Velocity after the jump, Energy dissipated in the jump.A9)

y1 = 1m

A1 = 3* 1 = 3m2

V1 = 18/3 = 6m/s

yh= A/T

For rectangular channel, yh = y

Therefore, Nf = 1.92 > 1.0 (supercritical flow)

Find y2 using the equation

y2 = 2.26 m

v2 = Q/A2 = 18/(3*2.26) = 2.65 m/s

loss of energy is computed using

E1 − E2 = ( y2 − y1)3 / 4y1y2

E1 – E2 = 0.22 m

Q10) Describe rapidly varying flow.A10) If water depth or velocity change abruptly over a short distance and the pressure distribution is not hydrostatic, the water surface profile is characterized as Rapidly Varying Flow (RVF). The occurrence of RVF is usually a local phenomenon. RVF can often be observed near the inlet and outlet of culverts, and wherever hydraulic jumps occur. Due to non-hydrostatic pressure distribution, rapidly varied flow can not be analyzed by using the same approach as that for parallel flow. In the past, these flows have been mainly investigated experimentally; and empirical relationships and other information in the form of charts and diagrams have been developed. Each particular phenomenon has been studied more or less in isolation, and a considerable amount of information is available for typical design applications. The rapidly varied flows have been analysed based on the Boussinesq and Fawer assumptions. In the Boussinesq assumption, the vertical flow velocity is assumed to vary linearly from zero at the channel bottom to the maximum at the free surface. In the Fawer assumption, this variation is assumed to be exponential. The rapidly varied flow usually occurs in a short distance. Therefore, the losses due to shear at the channel boundaries are small and maybe neglected in a typical analysis. However, because of sudden changes in the channel geometry, the flow may separate, and eddies and swirls may form. These phenomena complicate the flow pattern, and it becomes difficult to generalize the velocity distribution at a cross-section. Even in those cases where it may be possible to approximate the velocity distribution, the energy coefficient, α, and the momentum coefficient, β, are difficult to quantify and usually have a value significantly higher than unity. Because of separation zones, the formation of rollers and eddies, it becomes difficult to define the flow boundaries and to determine the average flow variables for a cross-section.

Sign Up