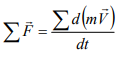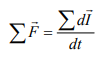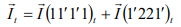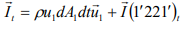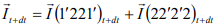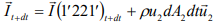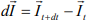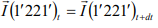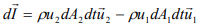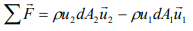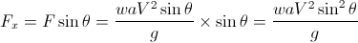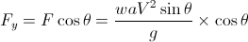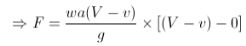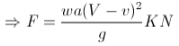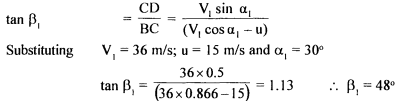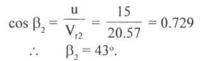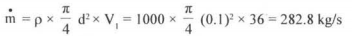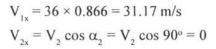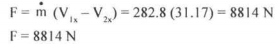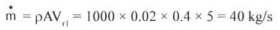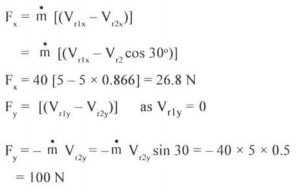undefined | unit 5 impact of jet

FM 2

UNIT-5IMPACT OF JET Q1) What is the impact of the jet? Derive impulse-momentum equation.A1) Impact of jet The liquid comes out in the form of a jet from the outlet of a nozzle which is fitted to a pipe through which the liquid is flowing under pressure. A jet is a stream of fluid that is projected into a surrounding medium, usually from some kind of a nozzle, aperture, or orifice. Jets can travel long distances without dissipating. Jet fluid has higher momentum compared to the surrounding fluid medium. In the case that the surrounding medium is assumed to be made up of the same fluid as the jet, and this fluid has a viscosity, the surrounding fluid is carried along with the jet in a process called entrainment.Impulse Momentum PrincipleThe impulse-momentum equation for fluid flow can be derived from the well-known Newton’s second law of motion. The resultant force Fˉ acting on a mass particle m is equal to the time rate of change of linear momentum of the particle:Fˉ= d(mVˉ)/dt This law applies equally well to a system of mass particles. The internal forces between any two mass particles of the system exist in pairs. They are both equal and opposite of each other and, therefore, will cancel out as outlined in Newton’s third law of motion. The external forces acting on mass particles of the system can then be summed up and equated to the time of change of the linear momentum of

the whole system,

If we define momentum by I˘=mVˉ, then

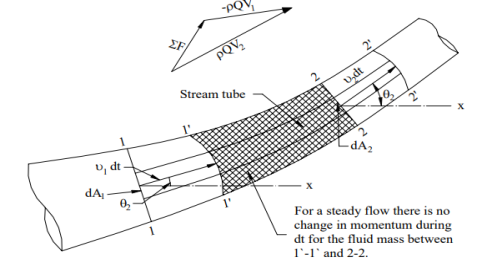
Extending Newton’s second law of motion to fluid flow problem, take as a free body the fluid mass included between sections 1-1 and 2-2 within a length of a flow channel.

The fluid mass of the free body 1-1 and 2-2 at time t1 moves to a new position 1’-1’ and 2’-2’ at time t2 when t2-t1 equals dt. Sections 1’-1’ and 2’-2’ are curved because the velocities of flow at these sections are non-uniform. It should be noted that, for a steady flow, the following continuity equation holds.

[Fluid mass within section 1-1 and 1’-1’] = [Fluid mass within section 2-2 and 2’-2’]

M (11′1′1) = M (22′2′2)

The momentum of the system at time t,

The momentum of the system at time t+dt,

Change of momentum at dt time,

Furthermore, when the flow is steady,

From the Last two equations

From previous equations,

This equation is known as the impulse-momentum equation. Q2) What are the various forces exerted by a jet? A2) The following are the cases of the impact of a jet, i.e. the force exerted by the jet on a plate: 1. Force exerted by the jet on a stationary plate a) Plate is vertical to the jet b) Plate is inclined to the jet c) Plate is curved2. Force exerted by the jet on a moving plate a) Plate is vertical to the jetb) Plate is inclined to the jet c) Plate is curved Q3) Derive the equation for the force exerted by the jet on a stationary vertical plate.A3) Consider a jet of water coming out from the nozzle strikes the vertical plate

V = velocity of jet, d = diameter of the jet, a = area of x – section of the jet.The force exerted by the jet on the plate in the direction of the jet. Fx = Rate of change of momentum in the direction of the force. Rate of change of momentum in the direction of force = initial momentum – final momentum/time = mass x initial velocity – mass x final velocity / time = mass/time (initial velocity – final velocity) = mass/ sec x (velocity of the jet before striking mass/ sec x (velocity of the jet before striking – final velocity of jet after striking) Q4) Describe the force of Jet Impinging on an Inclined Fixed Plate.A4) Consider a jet of water impinging normally on a fixed plate as shown in the figure.

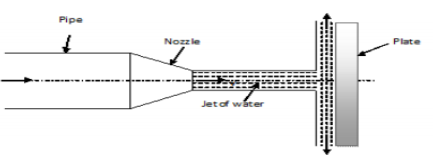
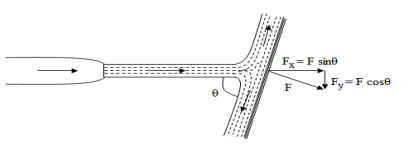
Let, • Ɵ = Angle at which the plate is inclined with the jet

Force exerted by the jet on the plane = waV2/g KN

Force exerted by the jet in a direction normal to the plate, F= waV2sin Ɵ/g and the force exerted by the jet in the direction of flow,

Similarly, the force exerted by the jet in a direction normal to flow,

Q5) How do you obtain the force of a jet on a moving plate?A5) Consider a jet of water imping normally on a plate. As a result of the impact of the jet, let the plate move in the direction of the jet as shown in fig 5-6.

Fig. 5-6 Jet impinging on a moving plateLet, v= Velocity of the plate, as a result of the impact of jet A little conversation will show that the relative velocity of the jet concerning the plate equal to (V-v) m/s. For analysis purposes, it will be assumed that the plate is fixed and the jet is moving with a velocity of (V-v) m/s. Therefore, the force exerted by the jet,F= mass of water flowing per second x Change of velocity

Q6) Derive force of jet impinging on a moving curved vane.A6) Consider a jet of water entering and leaving a moving curved vane as shown in the figure.

Jet impinging on moving curved vaneConsider a curved vane moving with a velocity v under the action of the dynamic thrust exerted by a jet of water gliding over it.Let V be the velocity of the jet at the inlet.Let Vr be the relative velocity of the jet for the vane.The shape of the vane and its position for the jet is so designed that the jet should just glide over it so that there will be no loss of energy due to shock. For this condition, the direction of the relative velocity Vr at the inlet should be along the tangent to the vane at the inlet.The relative velocity at the inlet is the vectorial difference between the velocity of the jet and the velocity of the vane at the inlet.

Q7) What is a Velocity diagram?A7) In turbomachinery, a velocity triangle or a velocity diagram is a triangle representing the various components of velocities of the working fluid in a turbomachine. Velocity triangles may be drawn for both the inlet and outlet sections of any turbomachine. The vector nature of velocity is utilized in the triangles, and the most basic form of a velocity triangle consists of the tangential velocity, the absolute velocity, and the relative velocity of the fluid making up three sides of the triangle. Consider turbomachine consisting of a stator and a rotor. The three points that are very much important to draw the velocity triangles are entry to the stator, the gap between the stator and rotor, and exit from the rotor. These points are labeled 3, 1, and 2 respectively in figure 3.2, and a combination of rotor and stator is called stage in turbomachines. The fluid enters the stator at point 3 but as the stator is not moving there is no relative motion between the incoming flow and the stator so there is no velocity triangle to draw at this point. At point 1 the flow leaves the stator and enters the rotor. Here there are two flow velocities, the absolute velocity of the flow (V) viewed from the point of view of the stationary stator and relative velocity of flow (Vr) viewed from the point of view of the moving rotor. The rotor is moving with a tangential velocity of magnitude U. At point 2 the flow leaves the rotor and exits the stage. Again there are two flow velocities, one by viewing from the moving rotor and another by viewing from outside the rotor where there is no motion.

Fig. Velocity triangles for a turbomachineTherefore velocity triangles can be drawn for the point 1 and point 2 as shown in the figure, the methodology for this is as follows: 1. Draw the flow that is known 2. Draw the blade speed 3. Close the triangle with the remaining vector 4. Check that the key rule applies:

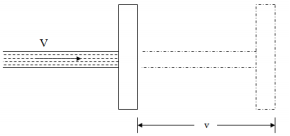
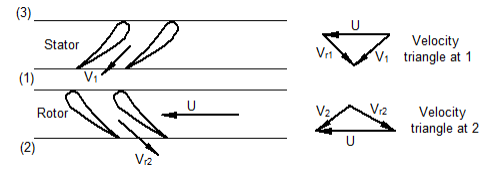
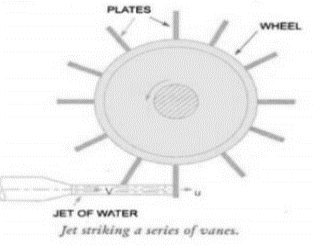
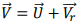The velocity triangles at the inlet and outlet of the rotor are of utmost importance in deciding the size of the turbomachine for the given power output. Q8) Describe the impact of jet on series of flat plates Mounted on a wheel.A8) The configuration of the system is shown in fig,. In this case, the plate fixed on the wheel moves with a velocity u in the direction of the jet. As one plate comes out of the jet, the jet strikes on the other plate, and the whole flow from the jet strikes the plate when all plates are considered.

Fig. Jet striking series of vanes

The velocity of the jet with which jet strikes the plate is the relative velocity of the jet which is (V-u)

The final velocity of the jet after striking the plate = V-u =0.

Change in velocity = initial relative velocity – Final relative velocity

= (V-u) – 0= V-u

Force acting on the plate = 𝑚̇ 𝑥 𝐶ℎ𝑎𝑛𝑔𝑒̇ 𝑖𝑛 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦

= 𝜌𝑎𝑉(𝑉 − 𝑢) Newtons

The efficiency of the system is given by

𝜂 = 𝑂𝑢𝑡𝑝𝑢𝑡 /𝐼𝑛𝑝𝑢𝑡 = 𝐹 𝑥 𝑢 /(1/2)𝑚𝑉2 = 𝜌𝑎𝑉(𝑉−𝑢)𝑢 /(1/2) 𝜌𝑎𝑉𝑉2

𝜂 = 2(𝑉−𝑢)𝑢 /𝑉2

For finding out the maximum velocity for the given input (V is constant),

The condition required is, 𝑑𝜂/𝑑𝑢 = 0

𝑑/𝑑𝑢 [𝑢(𝑉 − 𝑢)] = 0

V- 2u = 0

u = 𝑉/2

Corresponding maximum efficiency is given by

𝜂𝑚𝑎𝑥 = 2 (2𝑢−𝑢)𝑥 𝑢 /(2𝑉)2

= 0.5 𝜂𝑚𝑎𝑥

= 50%

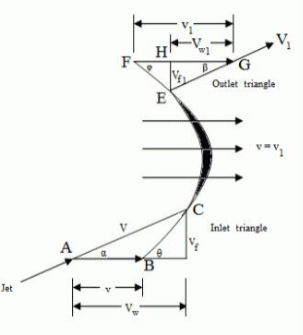
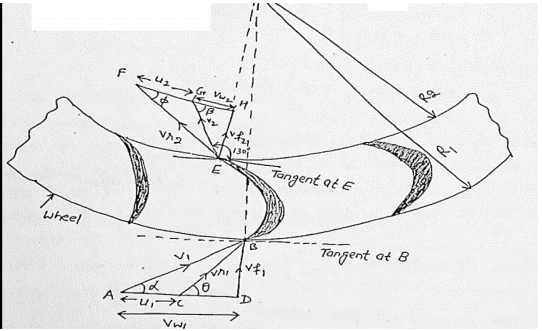
Q9) How do you calculate the force exerted on series of radial curved vanes?A9) Consider a series of radial curved vanes mounted on a wheel as shown in fig. The jet water impinges on the vane and the wheel starts rotating at a speed

Fig. Force exerted on series of radial curved vane

Let, 𝜔 = angular speed of the wheel

R1, R2 = Radii of the wheel at inlet and outlet of vane respectively

As vane are situated radially around the wheel blade velocities at inlet and outlet tip of vane would be different

u1 = 𝜔 R1 and u2 = 𝜔 R2

The flow system is inward or outward depending upon whether the jet enters the outer periphery or the inner periphery.

The mass of water striking/sec = mass of water issuing from the nozzle per second = 𝜌aV1

The momentum of water striking the vanes (in tangential direction) per second at the inlet

= 𝜌aV1 x Vw1

Similarly Momentum of water striking the vanes (in tangential direction) per second at the outlet

= 𝜌aV1 x (- Vw2) = - 𝜌aV1 x Vw2

-ve sign is taken as V2 at the outlet is in opposite direction.

Now, angular momentum per second at inlet = momentum at inlet x radius at inlet

= 𝜌aV1 x Vw1 x R1

angular momentum per second at outlet = 𝜌aV1 x Vw2 x R2

Torque exerted by water on the wheel,

T = rate of change of angular momentum

= (initial angular momentum/sec - final angular momentum/sec)

= 𝜌aV1 x Vw1 x R1 – (-𝜌aV1 x Vw2 x R2)

= 𝜌aV1 (Vw1 x R1 + Vw2 x R2)

W.D./sec on the wheel = T x 𝜔

= 𝜌aV1 (Vw1 x R1 + Vw2 x R2) x 𝜔

= 𝜌aV1 (Vw1 x 𝜔 R1 + Vw2 x 𝜔 R2)

= 𝜌aV1 (Vw1 x u1 + Vw2 x u2)

In case β is an obtuse angle,

then W.D./sec = 𝜌aV1 (Vw1 x u1 - Vw2 x u2)

If discharge is radial at outlet,

then β = 900 W.D./sec = 𝜌aV1 (Vw1 x u1) (Vw2 = 0)

Efficiency of radial curved vane

η = 𝑊.𝐷./ 𝑠𝑒𝑐 𝐾.𝐸./𝑠𝑒𝑐

= 𝜌aV1 (Vw1 x u1 ± Vw2 x u2)/ 𝟏/𝟐 𝜌aV3

= 2 (Vw1 x u1 ± Vw2 x u2) 𝑉2

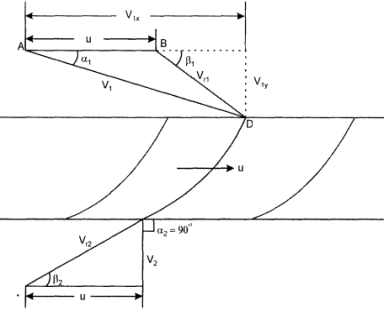
Q10) A jet of water 100 mm in diameter leaves a nozzle with a mean velocity of 36 m/s as shown in Fig. 2.23. It is deflected by a series of vanes moving with a velocity of 15 m/s in the direction at 30° to the direction of the jet so that it leaves the vane with an absolute velocity which is at right angles to the direction of the vane. Owing to friction the velocity of the fluid relative to the vanes at exit is equal to 0.85 of relative velocity at inlet. Calculate (a) inlet angle and outlet angle of the vane for no shock entry and exit. (b) the force exerted on the series of vanes in the direction of motion of vanes. A10)

Solution:

(a) With reference to the Fig. given quantities are:

VI = 36 m/s;

Vr2=0.85Vr1;

u = 15 m/s; d=IOOmm

α1= 30°, α2= 90°

To determine the inlet angle β1 consider the inlet velocity triangle ABD. The velocity of the fluid relative to the vane at the inlet in Vrl must be tangential to the vane and make an angle βI with the direction of motion

To determine outlet angle β2 as V2 has no component in the direction of motion, outlet angle β2 is given by

(b) Since the jet strikes series of vanes perhaps mounted on the periphery of a wheel so that each vane moves on its place is taken by the next in the series, the average length of the jet does not alter and the whole flow from the nozzle of diameter d is deflected by the vanes. The mass flow rate of the fluid from the nozzle

Velocity component of VI in direction of X = VI cos αl

Force on the direction of motion

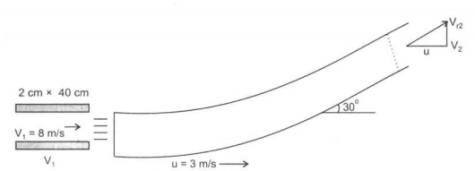
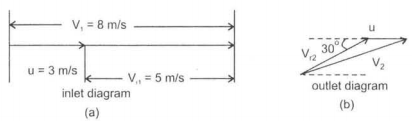
Q11) A deflector is shown in Fig. moves to the right at 3 m/s while the nozzle remains stationary. Determine the force components needed to move the deflector. The jet velocity is 8 m/s. The nozzle area is 2 cm x 40 cm.

A11)

Inlet triangle of velocity is a straight line as shown in Fig. (a). The outlet triangle of velocity is shown in Fig. (b).

Bernoulli's equation can be used to show that the velocity of the sheet VrI = Vr2 = 5 m/s as observed from the deflector.

Mass flow rate is calculated on velocity VrI = 5 m/s

Force in the x-direction

Fx = Mass flow rate x change of velocity

Sign Up