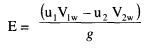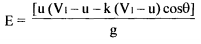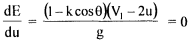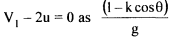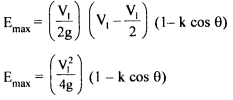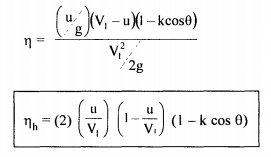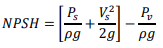|
) The total head available from the reservoir above the nozzle is H1 Head loss in pressure tunnel and penstock due to friction = hf Head loss in the nozzle = hn Net head available for power generation at the exit of nozzle = H
H=H1 - hf -hn
Where hf = flv2/2gd
Where l = length of penstock v = Velocity in penstock d = diameter of penstock f = coeff. of friction
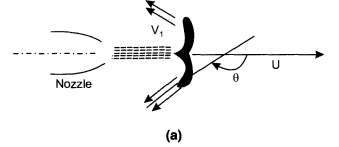
In practice, the penstock is usually sized so that at rated power the net head is usually 85-95% of the total head. The net head is taken to calculate the hydraulic efficiency of the turbine. The jet strikes the bucket at the center and takes a tum of almost 1800 and leaves on both sides of the bucket as shown in ( a), (b)
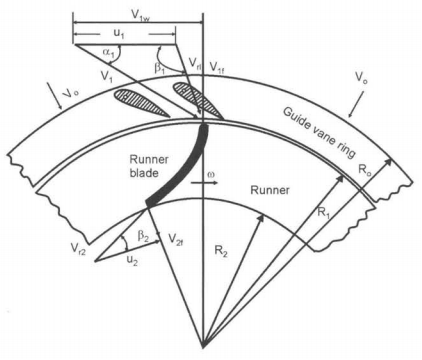
(a) Jet impingement (b) double hemispherical shape of buckets. The velocity of the jet is given by VI =√2gH The inlet and exit velocity diagrams are shown in the next fig. The total energy transferred to the wheel is given by Euler's Equation.
As the turbine is axial the tangential velocity is the same at the inlet and exit ul = u2 = U so that Euler's equation becomes
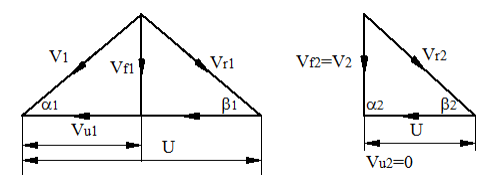
Velocity Diagram The inlet velocity triangle is a straight line, we have V rl = VI - u and VIw = VI Also, Vr2 = k Vri, where k is coefficient ot-velocity due to friction. The relative velocity vr2 is tangential to the exit tip of the buckets. Superimposing peripheral velocity u we obtain absolute velocity V2. The velocity Vr2 makes an angle θ with the central line of the bucket. Vr2 = k Vri = k(VI - u) thus V2w = u - Vr2 cos (π-θ) Vr2 = U + Vr2 cos θ V2w = U + k (VI - U ) cos θ Writing Euler's equation
Substituting, V2w = u + k(VI - u) cos θ ; as VIw = V1. we have
The equation shows that there is no energy transfer when the bucket velocity u is either zero or equal to jet velocity VI. It is reasonable to expect therefore the maximum energy transfer will occur at some intermediate velocity of the bucket velocity. Thus differentiating E for u and equating to zero for maximum energy transfer
Hence, We have u/V1=1/2 Thus tangential velocity is half the jet velocity for maximum energy transfer. Substituting this value in eq
Inlet kinetic energy to the jet= V12/2g Thus maximum theoretical hydraulic efficiency of Pelton wheel,
In an ideal case when θ = 180°, k = I; nmax = 100%. In practice, friction exists and the K value is in the region of 0.85 - 0.9 and also the value of θ = 165° to avoid interference between incoming and outgoing jets. Therefore u/V1 is always less than 0.5. For u/V1= 0.46 and θ = 165° , the maximum efficiency is around 90%. Rewriting the equation for Emax, E = u/g(VI - u) (I - kcos θ) and also K.E of jet = V12/2g and hydraulic efficiency as
|
|
|
|
|
A7) The following points should be considered while selecting the right type of hydraulic turbines for a hydroelectric power plant.
1) Specific speed:
High specific aped is essential where the head is low and output is large because otherwise, the rotational speed will be low which means the cost of turbo-generator and powerhouse will be high. On the other hand, there is practically no need of choosing a high value of specific speed for high installations, because even with lo specific speed high rotational speed can be attained with medium capacity plants.
2) Rotational speed:
Rotational speed depends upon a specific speed. Also the rotational speed of an electrical generator with which the turbine is to be directly coupled depends on the frequency and number of pairs of poles. The value of the specific speed adopted should be such that it will give the synchronous speed of the generator.
3) Efficiency:
The efficiency selected should be such that it gives the highest overall efficiency of various conditions.
4) Part load operation:
In general, the efficiency at part loads and overloads is less than that with rated (design) parameters. For the sake of the economy, the turbine should always run with maximum possible efficiency to get more revenue.
When the turbine has to run at part or overload conditions Deriaz turbine is employed. Similarly, for low heads, the Kaplan turbine will be useful for such purposes in place of the propeller turbine.
5) Cavitations:
The installation of water turbines of reaction type over the tailrace is affected by cavitations. The critical values of cavitation indices must be obtained to see that the turbine works in a safe zone. Such values of cavitation indices also affect the design of the turbine, especially of Kaplan, propeller, and bulb types.
6) Deposition of turbine shaft:
Experience has shown that the vertical shaft arrangement is better for large-sized reaction turbines, therefore, it is almost universally adopted, whereas, in the case of large size impulse turbines, horizontal shaft arrangement is preferable.
7) Available head and its fluctuation:
a) Very high (350m and above): for heads greater than 350m, Pelton Turbine is generally employed and practically there is no choice except in very special cases.
b) High heads (150 m to 350 m): in this range either Pelton or Francis turbine may employ. For higher specific needs Francis turbine is more compact and economical than the Pelton turbine that for the same working conditions would have to be much bigger and rather cumbersome.
c) Medium heads (60 m to 150 m): a Francis turbine is usually employed in this range. Whether a high or low specific speed would be used depends on the selection of the speed.
d) Low heads (below 60m): between 30m to 60m both Kaplan and Francis turbines may be used. Francis is more expensive but yields higher efficiency at part loads and overloads. It is therefore preferable for variable loads. Kaplan turbine is generally employed less than 30m. Propeller turbines are, however, commonly used for heads up to 15m. They are adopted only when there is practically no load variation. 8) Water quality: (i.e. sand content chemical or other impurities)
Quality of water is more crucial for the reactive turbine than in reaction turbines. Reactive turbines may undergo rapid wear in high-head reactive turbines.
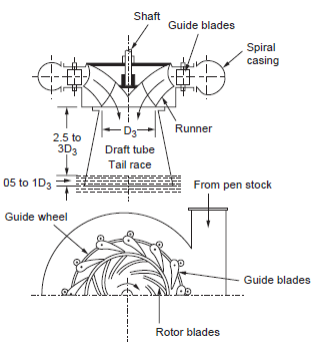
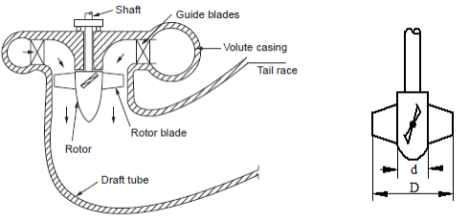
Q8) Write a short note on draft tubes in reaction hydraulic turbines. Explain the functions of a draft tube in a reaction hydraulic turbine.
A8) Water, after passing through the runner is discharged through a gradually expanding tube called a draft tube. The free end of the draft tube is submerged deep into the water. Thus the entire water passage from the headrace to the tailrace is completely closed and hence doesn’t come in contact with atmospheric air. It is a welded steel plate pipe or a concrete tunnel with a gradually increasing cross-sectional area at the outlet.
The functions of a draft tube are as follows,1. A reaction turbine is required to be installed above the tailrace level for easy of maintenance work, hence some head is lost. The draft tube recovers this head by reducing the pressure head at the outlet to below the atmospheric level. It increases the working head of the turbine by an amount equal to the height of the runner outlet above the tailrace. This creates a negative head or suction head. 2. Exit kinetic energy of water is a necessary loss in the case of the turbine. A draft tube recovers part of this exit kinetic energy. 3. The turbine can be installed at the tailrace level, above the tailrace level, or below the tailrace level. Q9) What do you mean by NPSH? Is it desirable to have a lower or higher value of NPSH? A9) It is the head required at the pump inlet to keep the local pressure everywhere inside the pump above the vapour pressure. Net positive suction head (NPSH) is defined as the difference between the pump’s suction stagnation pressure head and vapour pressure head.
|
|