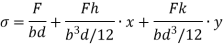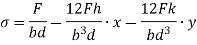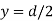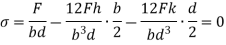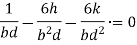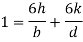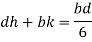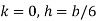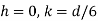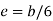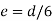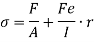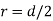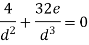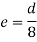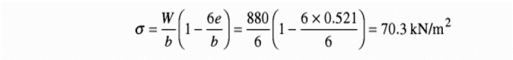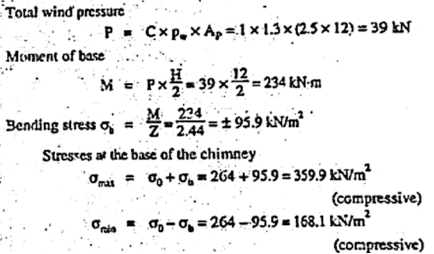undefined | unit 2 combined direct and bending stresses

Back to Study material

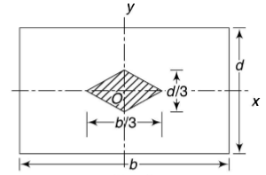
Unit-2Combined Direct and Bending StressesQ1) Explain the middle third rule for rectangular section.A1) Middle Third rule for rectangular sectionConsider the rectangular section with width b and depth d.

The tensile stresses may be developed if, x and y are negative.

In limiting cases if and ; and

This equation gives the limiting values of h and k. In each quadrant the load must lie in the line produced by this equation.

When and when

It shows that when the load lies on the either axis, it should lie on the middle third in the cross-section to avoid the tensile stress. Hence, the load must lie in the diamond area.

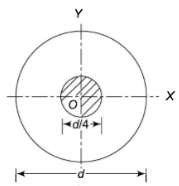
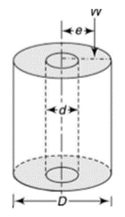
For the rectangular section, maximum eccentricity is in x-direction and in y-direction.

Explain the middle quarter rule for circular sections.

Middle Quarter rule for circular sectionConsider the circular section with diameter d as shown below

The maximum stress along any axis of diameter is

In limiting cases, and

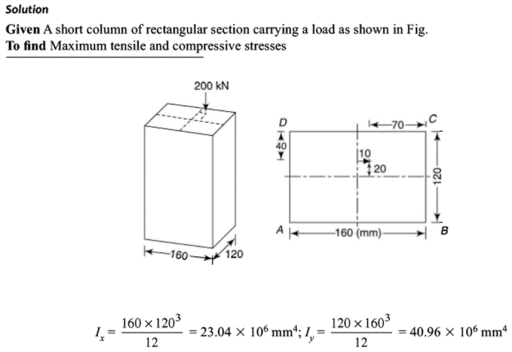
The equation gives the limiting value of eccentricity for all possible positions of the load. The kernel is the circle of diameter

with center O. To avoid tensile stress, load must lie within this section. Q2) A short column of rectangular section 160 mm x 120 mm carries a load of 200 kN. The load point is at a point 40 mm from the longer side and 70 mm from the shorter side. Determine the maximum tensile and compressive stresses in the section.A2)

Q3) A short column of external and internal diameters as D and d respectively carries an eccentric load W. Determine the maximum eccentricity which the load can have without producing the tension on the cross-section of the column.

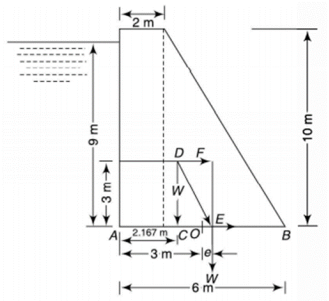
Q4) A gravity dam is 10 m high. Its width at the top and bottom is 2 m and 6 m respectively. Its water face is vertical and retains water to a depth of 9 m. Determine the maximum and minimum stress values at the base. The weight of the dam is 22 kN/m3 and specific weight of water 9.81 kN/m3.

A4)

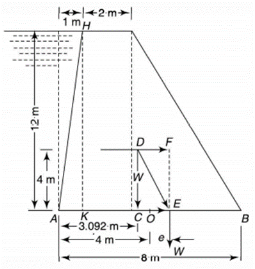
Q5) A masonry dam trapezoidal in section 12 m high. It is 2 m wide at the top and 8 m wide at the bottom. The face exposed to water has a slope of 1 horizontal to 12 vertical. The water level in the dam is up to the top of dam. The weight of the masonry is 25 kN/m3 and specific weight of water is 9.81 kN/m3. Determine the maximum and minimum stress values at the base.

A5)

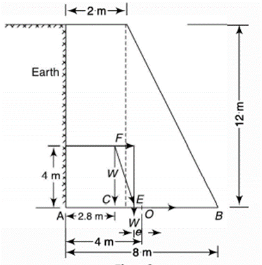
Q6) A 12 m high masonry retaining wall of trapezoidal section has a width of 2 m at the top and 8 m at the bottom. The retaining surface is vertical and the wall retains earth which is level up to the top. Determine the maximum and minimum stresses at the base. The densities of the earth and the masonry are 14 kN/m3 and 25 kN/m3 respectively and the angle of repose of the earth is 30o.

A6)

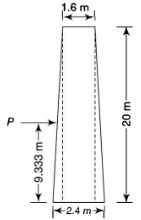
Q7) A masonry chimney that is 20 m high tapers from 2.4 m external diameter at the base of 1.6 m diameter at the top. The weight of the chimney is 1200 kN. Determine the uniform horizontal wind pressure so that no tension occurs at the base.

A7)

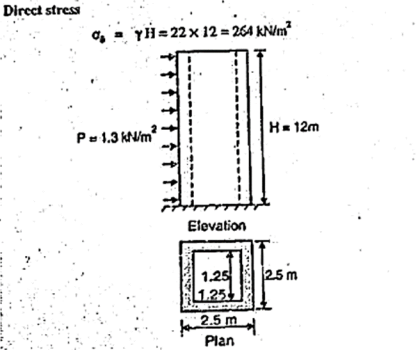
Q8) A square chimney 12 m high has an opening 1.25 m x 1.25 m inside. The external dimensions are 2.5 m x 2.5 m. The wind intensity is 1.3 kN/m2 on projected area specific weight of masonry is 22 kN/m3. Calculate maximum and minimum intensities of stresses at the base of the chimney.A8)

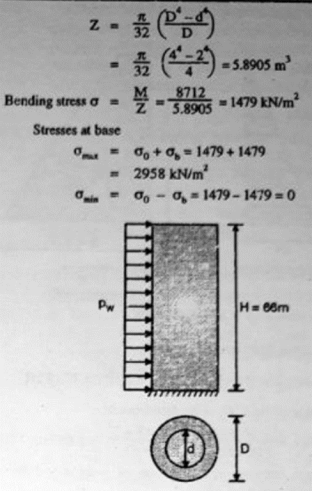
Q9) A masonry chimney has external diameter 4 m and internal diameter 2 m is subjected to uniform wind pressure of 1500 N/m2 over an entire height of 66 m. Determine maximum and minimum stresses at base. Unit weight of masonry wall is 22.41 kN/m2, take C=2/3A9)

Sign Up