Q3 Draw the influence line diagram using Muller Breslau’s principle for the propped cantilever of span L shown in figure fixed at A and simply supported at B for

Back to Study material

Unit - 3Influence Line Diagram Q1) Explain Muller Breslau’s Principle.A1) Muller Breslau’s Principle:It states that, “The influence line for any function such as support reaction, shear force or bending moment is any redundant member of a statically indeterminate structure is given by the deflection curve for the structure, when a unit load replaces the redundant member, the scale for deflection being so chosen that the deflection at the point of redundancy where the unit load is applied as unity.”Proof:Consider a continuous beam ABC, freely supported at A and C, continuous over B.Let unit load moves along beam ABC from A to C.Consider a section x-x at a distance x from A.To plot the ILD fro reaction RBRemove the support B, find out the deflection at B.Let the deflection is yBxNow, apply unit load at BFind out the deflection at x due to unit load acting at B, say yxBFind out the deflection at B due to unit load at B, say, yBBAs per Maxwell’s reciprocal theorem,

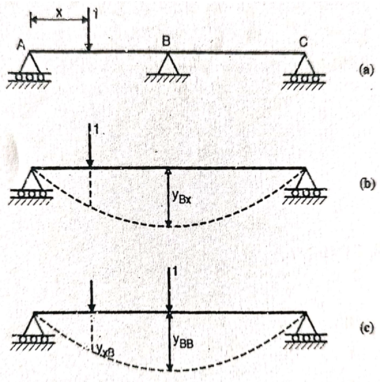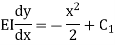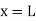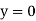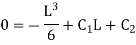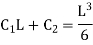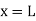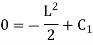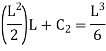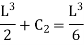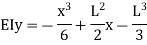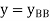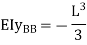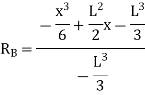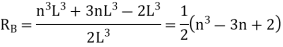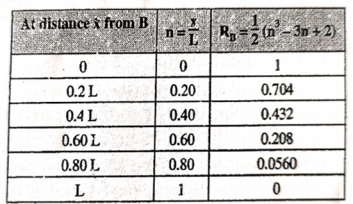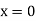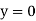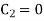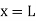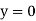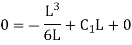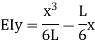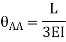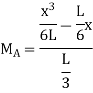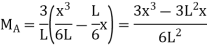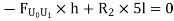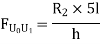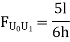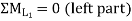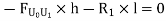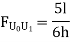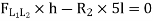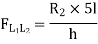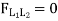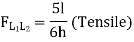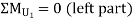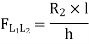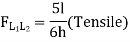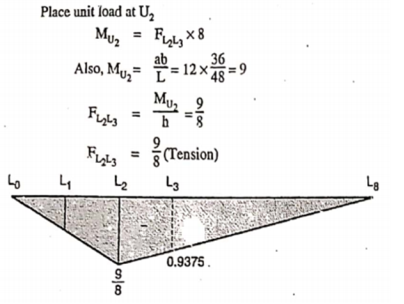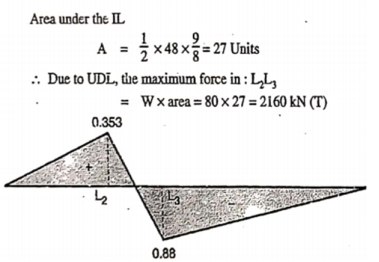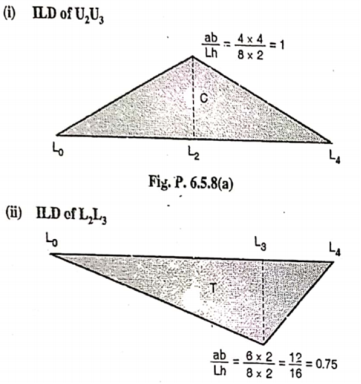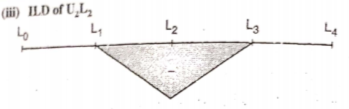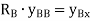
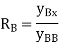This expression gives the reaction at BTo plot ILD for RB, take yBB = 1

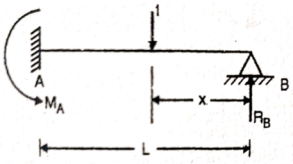
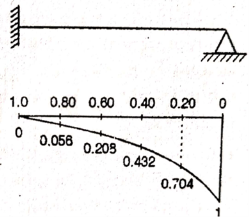
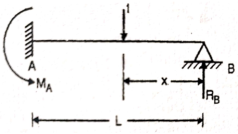
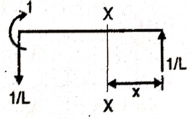
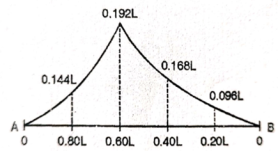
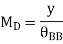Similarly, to obtain ILD for BM, instead of applying unit load, unit moment is applied at point of required BM. The moment at D

Q2) Draw the influence line diagram using Muller Breslau’s principle for the propped cantilever of span L shown in figure fixed at A and simply supported at B for reaction at B.

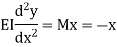
S2)Remove the support B and apply unit load at BMoment C is

Integrating above equation,

Integrating it again we get,

Applying boundary condition, at support A, both slope and deflection is zero.

Hence, at

Substituting above value,

And at

Substituting above values,

Therefore,

Substituting values of C1 and C2

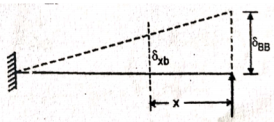
This is the general expression of deflection

Deflection at B:

At B, ,

Substituting above value in expression of deflection,

We know that, reaction at B,

Put

ILD for RB:Prepare a table of the values of RB for n ranging from 0 to 1, as under

The ILD for RB can now be plotted as shown in figure below

Q3) Draw the influence line diagram using Muller Breslau’s principle for the propped cantilever of span L shown in figure fixed at A and simply supported at B for moment at A

S3)

Remove fixed support A

Apply unit couple at A

iii. Determine slope at A

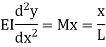Integrating this equation w.r.t. x

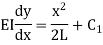Integrating it again we get,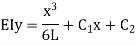

Applying boundary condition,

Hence, at B therefore,

At B

Substituting above value,

Substituting values of C1 and C2

This is the general expression of deflection

And,

At A,

Slope at A

ILD for moment A

ILD for moment at A

Put

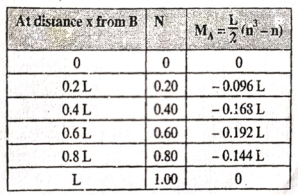
Prepare a table of the values of MA for n ranging from 0 to 1, as under

The ILD for moment at A can now be plotted as shown in figure below

Q4) Explain Influence Line diagram and give its uses.A4) The loads acting on structures are broadly classified as dead loads of self-weight and live loads or superimposed loads. Dead loads are those which do not change their position but live loads which can change their position during the life of the structures. When the structure subjected to moving type of load, the reactions at supports, shear force, bending moment and deflections vary with varying position of load system.The graphical representation of such variation is called as influence line or influence line diagram (ILD). The designer analyses the structures by drawing such type of graph to get critical position of loads.Thus, the influence line diagram (ILD) may also be defined as a graph of stress resultants like a resultant like a reaction at supports, shear force at section, bending moment at a section for various positions of a unit load on the span of structure.Uses of ILD:

To determinate reaction at supports for a given system of loads.

To determinate the position of load for the maximum reaction.

To determinate shear force and BM at any section for the given system of loading.

To determinate the position of loads for maximum SF and BM at a section.

Q5) Determine the influence line diagram for the forces of top members of the N type through 6 panels l at each as shown in figure.

S5)ILD for Top chord members:Take the section 1 – 1 as shown in above figure. Section 1 – 1 cuts three members. To find forces in U1 U2. We have to take moment all forces about L1 because the remaining two parts are passing through L1, so moment of that member force are zero. When unit load is in left part, consider right part is in equilibrium and vice versa.

When unit load is at L0, R2 = 0

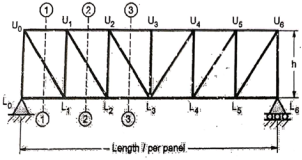
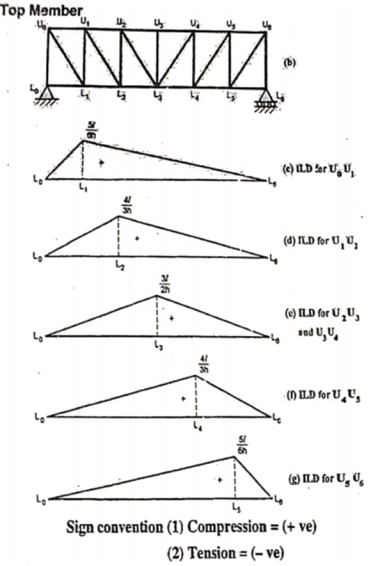
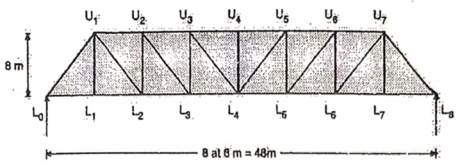
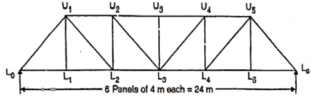
b. When unit load is at L1, R2 = 1/6

c. When unit load is in portion L1 to L6, taking moment about L1 we get,

When unit load is at L1, R1 = 5/6

When unit load is at L6, R1 = 0

Thus, it is similar to ILD for the moment at L1 divided by height. Similarly, ILD for U1 U2, U2 U3, U3 U4, U4 U5 and U5 U6 may be found by using ILD for the bending moments at L2, L3, L4 and L5 respectively.

Q6) Determine the influence line diagram for the forces of bottom members of the N type through 6 panels l at each as shown in figure.

S6)ILD for bottom chord member

ILD for L0L1: There should not be any force in member L0L1, through the unit load moves to any panel point. As unit load is vertical, so at the joint L0, no horizontal member or force acts other than L0L1.

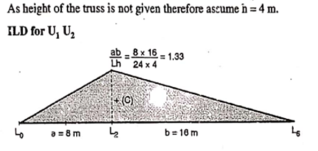
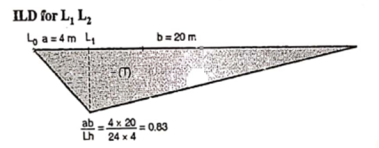
By observation

Similarly,

ii. ILD for L1 L2 : When unit load is on left part of section, consider right part of section in equilibrium section from figure (h)

When unit load is at L0, R2 = 0

When unit load is at L1, R2 = 5/6

When unit load is on right part,

When unit load is at L1, R2 = 5/6

When unit load is at L6, R1 = 0

Thus, it is similar to ILD of the bending moment at U1 divided by height. Similarly, ILD for L2 L3, L3 L4 and L4 L5 may be found by using ILD for the bending moments at U2, U4 and U5 respectively as shown in figure (k), (l) and (m).

Q7) A Pratt truss of 48 span, has eight panels of 6m each. The height of the truss is 8m. Draw the IL for the force in bottom chord member and diagonal of third panel from left. Also calculate the maximum force in the bottom member of third panel for a UDL of 80 kN/m, longer than the span.

S7)

Q8) Draw influence line diagram for members U2U3, L2L3 and U2L2 of a truss as shown in figure below

S8)

Q9) Draw influence line diagram for members U1U2, L1L2 and U1L2 of a truss as shown in figure below

S9)

Sign Up